Ulrikes Papierkegel: Unterschied zwischen den Versionen
Aus DMUW-Wiki
K |
K |
||
| (17 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
<div style="border: 2px solid #0000EE ; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid #0000EE ; background-color:#ffffff; padding:7px;"> | ||
<div style="border: 2px solid #0000EE ; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid #0000EE ; background-color:#ffffff; padding:7px;"> | ||
| + | [[Bild:Dorothea_Rauscher_Papierkegel.png|Papierkegel|right|350px]] | ||
| − | Ulrike hat einen | + | <br> |
| + | '''Ulrike hat aus buntem Papier einen Kegel gebastelt.''' | ||
| − | + | <br> | |
| + | '''Durch Abmessen mit einem Lineal hat sie folgende Maße ermittelt:''' | ||
| + | <br> | ||
| + | '''r = 3 cm und s = 7 cm.''' | ||
| + | <br> | ||
| + | '''Mit dem Lineal konnte sie aber nicht die Höhe des Kegels bestimmen.''' | ||
| − | < | + | <br> |
| − | + | '''Diese möchte Ulrike nun rechnerisch ermitteln.''' | |
| − | + | <br> | |
| − | + | '''Dabei benötigt sie einen wichtigen geometrischen Satz!''' | |
| − | + | <br> | |
| + | '''Weißt du, welchen geometrischen Satz Ulrike verwenden muss, um die Höhe des Kegels bestimmten zu können?''' | ||
| − | + | <br> | |
| − | '' | + | ''(Bringe die Buchstaben in die richtige Reihenfolge!)'' |
| + | <br> | ||
| + | <div class="schuettel-quiz"> | ||
| + | Ulrike muss den Satz des '''Pythagoras''' verwenden, um die Höhe des Kegels zu berechnen. | ||
| + | </div> | ||
| + | <br> | ||
| + | [[Bild:Kegel_19.10.09_Dorothea_Rauscher.png|Kegelino|right|200px]] | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <quiz display ="simple"> | ||
| + | { '''Bestimme die Höhe des Papierkegels und kreuze die richtige Antwort an!''' | ||
| + | <br> | ||
| + | ''(Runde auf eine ganze Zahl!)'' | ||
| type="[]" } | | type="[]" } | ||
| − | - h = | + | - h = 4 cm |
| − | + | - h = 40 cm | |
| − | - h = | + | |
|| Beinahe richtig! Du musst nur noch die Wurzel ziehen! | || Beinahe richtig! Du musst nur noch die Wurzel ziehen! | ||
| − | + h = 6 | + | + h = 6 cm |
| − | - h = | + | - h = 8 cm |
| − | || Achtung: | + | || Achtung: Du musst minus rechnen! |
| − | { '''Wie groß ist | + | { '''Nachdem du die Höhe berechnet hast, kannst du das Volumen bestimmen.''' |
| + | <br> | ||
| + | '''Wie groß ist dieses Volumen?''' | ||
| + | <br> | ||
| + | ''(Runde auf eine ganze Zahl!)'' | ||
| type="{}" } | | type="{}" } | ||
| − | Das Volumen beträgt { | + | Das Volumen beträgt { 57 } cm<sup>3</sup>. |
</quiz> | </quiz> | ||
| − | + | <br> | |
</div> | </div> | ||
</div> | </div> | ||
| − | |||
<br> | <br> | ||
| − | < | + | <br> |
| − | + | ||
<div align="left">[[Benutzer:Dorothea Rauscher/Würfelaufgabe 1|<math>\Leftarrow</math> Zurück zur vorherigen Aufgabe]]</div> | <div align="left">[[Benutzer:Dorothea Rauscher/Würfelaufgabe 1|<math>\Leftarrow</math> Zurück zur vorherigen Aufgabe]]</div> | ||
| + | <br> | ||
| + | <div align="left">[[Benutzer:Dorothea Rauscher/Dose|<math>\Rightarrow</math> Weiter zur nächsten Aufgabe]]</div> | ||
Aktuelle Version vom 14. Dezember 2009, 21:26 Uhr
PAPIERKEGEL
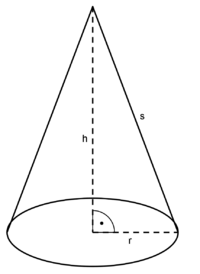
Ulrike hat aus buntem Papier einen Kegel gebastelt.
Durch Abmessen mit einem Lineal hat sie folgende Maße ermittelt:
r = 3 cm und s = 7 cm.
Mit dem Lineal konnte sie aber nicht die Höhe des Kegels bestimmen.
Diese möchte Ulrike nun rechnerisch ermitteln.
Dabei benötigt sie einen wichtigen geometrischen Satz!
Weißt du, welchen geometrischen Satz Ulrike verwenden muss, um die Höhe des Kegels bestimmten zu können?
(Bringe die Buchstaben in die richtige Reihenfolge!)
Ulrike muss den Satz des Pythagoras verwenden, um die Höhe des Kegels zu berechnen.

 Zurück zur vorherigen Aufgabe
Zurück zur vorherigen Aufgabe Weiter zur nächsten Aufgabe
Weiter zur nächsten Aufgabe
