Praktische Grenzen der Berechenbarkeit: Unterschied zwischen den Versionen
(→Bubble Sort) |
(→Lineare Suche) |
||
| Zeile 58: | Zeile 58: | ||
* <math>T_{average}(n)=4\cdot n - 1</math> | * <math>T_{average}(n)=4\cdot n - 1</math> | ||
* <math>T_{worst}(n)= 7\cdot n - 4</math> | * <math>T_{worst}(n)= 7\cdot n - 4</math> | ||
| + | |||
| + | |||
| + | == <math>\mathcal{O}</math>-Notation == | ||
== Bubble Sort == | == Bubble Sort == | ||
Version vom 21. September 2009, 21:04 Uhr
Inhaltsverzeichnis |
Motivation
Bei der Entwicklung eines effizienten Algorithmus spielt die Komplexitätstheorie eine große Rolle. Sie dient der Bewertung von Programmen und ermöglicht den Vergleich verschiedener Algorithmen bezüglich ihrer Laufzeit oder ihrem Speicherbedarf. Hierzu führt man, in Anlehnung an die Mathematik, Funktionsklassen ein, um die Algorithmen zu klassifizieren.
Ein Algorithmus heißt effizient, wenn er ein Problem mit möglichst geringem Ressourcenverbrauch (Zeit oder Speicher) löst.
Funktionsgraphen
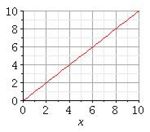
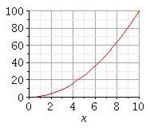
Wie gut kennst du noch die Funktionsgraphen und Funktionsnamen? Ordne den Funktionsgraphen die zugehörigen Funktionsnamen und Funktionsterme zu!
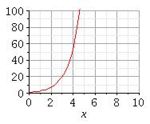 |
Exponentialfunktion | 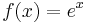
|
 |
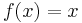 |
Lineare Funktion |
 |
Potenzfunktion | 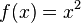
|
Lineare Suche
Der unten stehende Algorithmus durchsucht ein gegebenes Array a nach einem Objekt x.
Algorithmus Lineare_Suche
Eingabe: ein Array a der Länge n und ein zu suchendes Objekt x
Ausgabe: true, wenn es ein j, 1 <= j <= n gibt mit a[j] = x
j := 1
gefunden := (a[j] = x)
wiederhole
j := j + 1
gefunden := (a[j] = x)
solange j =< n
return gefunden
Der Algorithmus geht die Elemente des Arrays der Reihe nach durch. Dabei vergleicht er jedes Element mit dem Objekt x. Das Programm endet, sobald x gefunden oder das Ende des Arrays erreicht worden ist.
Zur Analyse der Laufzeit des Algorithmus zählt man die elementaren Rechenoperationen. Hierzu zählen:
- Vergleiche wie "<", ">", "=", "and", "not",...
- Wertzuweisungen wie ":="
- Rechenoperationen wie "+", "-", "*", "/",...
Die Zahl der benötigten Rechenoperationen hängt offensichtlich von der Größe des Array und ob bzw. an welcher Stelle im Array das Objekt x vorkommt.
Im besten Fall (englisch "best case") benötigt man also sechs elementare Rechenoperationen. Dies ist der Fall wenn das gesuchte Objekt im ersten Arrayfeld ist. Hier wird die while-Schleife nicht durchlaufen.
Im schlechtesten Fall wird die while-Schleife (n-1)-mal durchlaufen. Dies ist der Fall, wenn das gesuchte Objekt x überhaupt nicht im Array vorhanden ist. Dann benötigt man 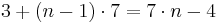 elementare Rechenoperationen.
elementare Rechenoperationen.
Interessant ist auch der durchschnittliche Fall (englisch "average case"). Hier wird die durchschnittliche Laufzeit über alle Möglichkeiten unter Berücksichtung der Wahrscheinlichkeit für die Eingabe a gemittelt. Man benötigt im Durchschnitt 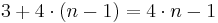 Rechenschritte.
Rechenschritte.
Mit 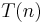 wird die Anzahl der elementaren Rechenoperationen in Abhängigkeit von der Länge des Arrays bezeichnet.
wird die Anzahl der elementaren Rechenoperationen in Abhängigkeit von der Länge des Arrays bezeichnet.
Zusammenfassend erhalten wir:
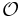 -Notation
-Notation
Bubble Sort
Sortierverfahren spielen in der Praxis eine wichtige Rolle. Bubble-Sort ist eines der einfacheren Sortierverfahren. Der Name kommt daher, dass große Elemente wie Luftblasen nach oben steigen. In diesem Video kann man die Funktionsweise anschaulich sehen.
Algorithmus BubbleSort
Eingabe: ein Array der Länge n
Ausgabe: ein aufsteigend sortiertes Array
wiederhole
vertauscht := falsch
für jedes i von 1 bis n - 1 wiederhole
falls A[ i ] > A[ i + 1 ] dann
vertausche( A[ i ], A[ i + 1 ] )
vertauscht := wahr
ende falls
ende für
n := n - 1
solange vertauscht und n >= 1
Die äußerste Schleife durchläuft die zu sortierenden Daten, bis keine Vertauschungen mehr nötig sind. In dieser Schleife wird das Feld jeweils einmal durchlaufen und es werden zwei benachbarte Daten vertauscht, wenn sie in falscher Reihenfolge stehen.
Zur Laufzeit:
Im schlechtesten Fall ist das Array absteigende sortiert. Dann steigt das erste Element von Feld 1 zu Feld n auf. Das zweite Element steigt dann von Feld 1 bis Feld n-1 auf und so weiter bis das Array aufsteigend sortiert ist. Es werden dann also für das erste Element n-1 Vertauschungen , für das zweite Element n-2 Vertauschungen, für das dritte Element n-3 Vertauschunge usw. durchgeführt. Beim letzten Element muss dann keine Vertauschung mehr durchgeführt werden. Insgesamt sind das dann 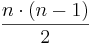 Vertauschungen. BubbleSort hat dann eine Laufzeit von
Vertauschungen. BubbleSort hat dann eine Laufzeit von 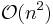 .
.
Im besten Fall ist das Array bereits aufsteigend sortiert. Dann wird das Array genau einmal durchlaufen und dabei feststellen, dass das Array bereits sortiert ist. BubbleSort hat dann eine Laufzeit von 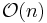 .
.
Türme von Hanoi
Das Spiel Türme von Hanoi besteht aus drei Stäben A,B und C, auf die verschieden große, gelochte Scheiben gesteckt werden können. Ziel des Spieles ist es, denn Stapel von Stab A auf Stab C zu verschieben. Dabei darf immer nur eine Scheibe auf eine anderen Stab gesteckt werden, wobei auf dem Zielstab keine kleinere Scheibe sein darf. Die Scheiben sind auf jedem Stab also der Größe nach geordnet.
Zusatzinformation:
Die Originalversion der Türme von Hanoi wurde von buddhistischen Mönchen ausgedacht. Dabei gab es ebenfalls 3 Stäbe, aber 64 Scheiben. Die Mönche prophezeiten das Ende der Welt, falls diese Aufgabe gelöst werde. Für die Lösung benötigt man mehr als 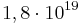 Scheibenbewegungen. Würde ein Mensch für eine Scheibenbewegung 1 Sekunde benötigen, würde das Lösen der Aufgabe 584.942.417.355 Jahre dauern, ohne auch nur geschlafen zu haben.
Scheibenbewegungen. Würde ein Mensch für eine Scheibenbewegung 1 Sekunde benötigen, würde das Lösen der Aufgabe 584.942.417.355 Jahre dauern, ohne auch nur geschlafen zu haben.
Wachstum von Funktionen
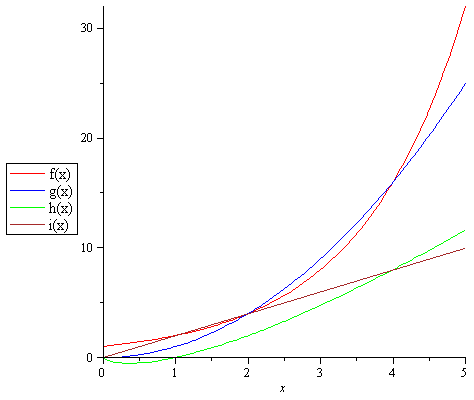
Gegeben sind die untenstehenden Funktionen. Ab welchem ganzzahligen 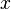 ist das exponentielle Wachstum von
ist das exponentielle Wachstum von 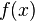 schlechter als das polynomielle der Funktionen
schlechter als das polynomielle der Funktionen 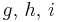 ?
?
(Hinweis: Stelle zur Bestimmung eine Wertetabelle auf oder löse die Aufgabe graphisch!)
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
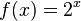 |
2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 |
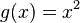 |
1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 |
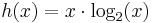 |
0 | 2 | 4,75 | 8 | 11,61 | 15,51 | 19,65 | 24 | 28,53 |
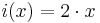 |
2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
Tabelle als Lückentext zum Ausfüllen
Reiskörner auf einem Schachbrett
Spielstellungen beim Schach
In den Nachrichten liest man von Zeit zu Zeit einen Artikel über Schach-Matches zwischen Schachgroßmeistern wie "Garri Kasparow" und Supercomputern wie "Deep Blue". Doch warum braucht man dazu Supercomputer? Und warum gewinnt der Computer nicht immer? Die Antwort auf diese Frage kannst du dir vielleicht schon nach dieser Aufgabe selbst beantworten!
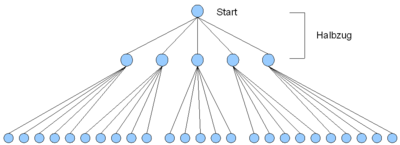
Ein Computerschachprogramm baut sich für jede Spielsituation einen Spielbaum auf und analysiert mit diesem, welcher Zug den größten Erfolg bringt. Um die Größe eines solchen Spielbaums geht es in dieser Aufgabe:
- Wie viele Knoten hat ein Schachspielbaum, bei dem jeder Halbzug (d.h. schwarz oder weiß ist am Zug) 5 Zugmöglichkeiten hat und ein Spiel im Durchschnitt nach 60 Halbzügen beendet ist?
- Kann man diesen Spielbaum auf einer handelsüblichen Festplatte speichern, wenn pro Knoten des Spielbaums 1 Byte Speicherplatz benötigt wird?
Für die Speicherung eines solchen Spielbaumes würde man ungefähr 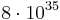 GB benötigen. Eine Studie von IDC hat für 2007 prognostiziert, dass der weltweit verfügbare Speicherplatz
GB benötigen. Eine Studie von IDC hat für 2007 prognostiziert, dass der weltweit verfügbare Speicherplatz 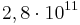 GB beträgt. Es ist also nicht möglich einen solchen Spielbaum zu speichern.
GB beträgt. Es ist also nicht möglich einen solchen Spielbaum zu speichern.
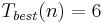
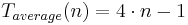


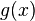 für
für 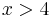 ,
,
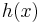 für
für 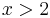 ,
,
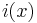 für
für