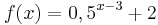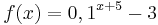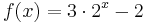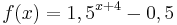Trigonometrie: Unterschied zwischen den Versionen
Aus DMUW-Wiki
| Zeile 26: | Zeile 26: | ||
Als erstes schauen wir uns an, welche Bedeutung Sinus, Cosinus und Tangens am Einheitskreis haben. Klick dich durch! | Als erstes schauen wir uns an, welche Bedeutung Sinus, Cosinus und Tangens am Einheitskreis haben. Klick dich durch! | ||
|} | |} | ||
| − | {{#slideshare: | + | {{#slideshare:sinuskosinustangens-100603045012-phpapp02}} |
<ggb_applet height="600" width="1000" showMenuBar="true" showResetIcon="true" filename="Peter Fischer_Einheitskreis.ggb" /> | <ggb_applet height="600" width="1000" showMenuBar="true" showResetIcon="true" filename="Peter Fischer_Einheitskreis.ggb" /> | ||
| Zeile 51: | Zeile 51: | ||
</div> | </div> | ||
| − | + | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | |
{| border="1" | {| border="1" | ||
! width="12" style="background-color:#FFD700;"| | ! width="12" style="background-color:#FFD700;"| | ||
| − | | width="1000" style="text-align:left" style="background-color:#FFEC8B;"| '''Aufgabe | + | | width="1000" style="text-align:left" style="background-color:#FFEC8B;"| '''Aufgabe 2 [[Bild:Peter_Fischer_Papier.png|40px]] ''' |
-------- | -------- | ||
Berechnungen zu Exponentialfunktionen. | Berechnungen zu Exponentialfunktionen. | ||
| Zeile 71: | Zeile 71: | ||
</quiz> | </quiz> | ||
| − | + | <poem> | |
'''Weiter gehts zu [[Trigonometrische Funktionen]]''' | '''Weiter gehts zu [[Trigonometrische Funktionen]]''' | ||
| + | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
| + | </poem> | ||
<div style="background:#FFD700;text-align:center;color: #fff;font-weight:bold;font-size:125%;margin: 10px 5px 0px 0; padding: 4px 4px 4px 14px;">Potenzen und Potenzfunktionen</div> | <div style="background:#FFD700;text-align:center;color: #fff;font-weight:bold;font-size:125%;margin: 10px 5px 0px 0; padding: 4px 4px 4px 14px;">Potenzen und Potenzfunktionen</div> | ||
<div style="margin: 0 5px 5px 0; padding: 1em 1em 1em 1em; text-align:center; border: 1px solid :#FFD700; background-color:#f6fcfe;"> | <div style="margin: 0 5px 5px 0; padding: 1em 1em 1em 1em; text-align:center; border: 1px solid :#FFD700; background-color:#f6fcfe;"> | ||
[[LERNPFAD]] | [[Trigonometrie]] | [[Trigonometrische Funktionen]] | [[Berechnungen in Dreiecken]] | [[Skalarprodukt]] | [[Exkurs: Figuren und ihre Eigenschaften]] </div><noinclude> | [[LERNPFAD]] | [[Trigonometrie]] | [[Trigonometrische Funktionen]] | [[Berechnungen in Dreiecken]] | [[Skalarprodukt]] | [[Exkurs: Figuren und ihre Eigenschaften]] </div><noinclude> | ||
Version vom 3. Juni 2010, 19:17 Uhr
Trigonometrie
| Arbeitsauftrag
Als erstes schauen wir uns an, welche Bedeutung Sinus, Cosinus und Tangens am Einheitskreis haben. Klick dich durch! |
{{#slideshare:sinuskosinustangens-100603045012-phpapp02}}
Aufgaben
Hier warten nun Aufgaben zu Exponentialfunktionen, diese sind auch sehr häufig in der Abschlussprüfugn zu finden!
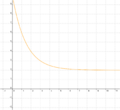
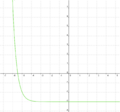
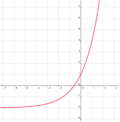
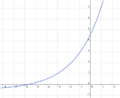
| Aufgabe 1
Ordne den Funktionsgleichungen ihre Graphen zu. Los geht's! |
Leerzeile
| Aufgabe 2 Berechnungen zu Exponentialfunktionen. |
Weiter gehts zu Trigonometrische Funktionen
Leerzeile
Potenzen und Potenzfunktionen