Trigonometrie: Unterschied zwischen den Versionen
K (linkfix) |
|||
| (19 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | {{Vorlage:Trigonometrie1}} | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | ==Trigonometrie== | + | <!-- |
| + | ==Trigonometrie== --> | ||
{| border="0" | {| border="0" | ||
! width="12" style="background-color:#FFD700;"| | ! width="12" style="background-color:#FFD700;"| | ||
| − | | width=" | + | | width="900" style="text-align:left"| '''Arbeitsauftrag''' |
-------- | -------- | ||
Als erstes schauen wir uns an, welche Bedeutung Sinus, Cosinus und Tangens am Einheitskreis haben. Anschließend wird der Umgang mit diesen Werkzeugen zur Winkelberechnung erklärt. Klick dich durch! | Als erstes schauen wir uns an, welche Bedeutung Sinus, Cosinus und Tangens am Einheitskreis haben. Anschließend wird der Umgang mit diesen Werkzeugen zur Winkelberechnung erklärt. Klick dich durch! | ||
|} | |} | ||
| − | |||
| − | |||
<poem> | <poem> | ||
| − | <ggb_applet height=" | + | :<iframe src="//www.slideshare.net/slideshow/embed_code/key/lI99WfoMJRbxdd" width="595" height="485" frameborder="0" marginwidth="0" marginheight="0" scrolling="no" style="border:1px solid #CCC; border-width:1px; margin-bottom:5px; max-width: 100%;" allowfullscreen> </iframe> |
| + | :[https://www.slideshare.net/fischernet/potenzfunktion-4978456 Potenzfunktion] | ||
| + | |||
| + | Falls die Präsentation nicht geladen werden kann, kannst du sie auch als PDF anschauen. Einfach anklicken. | ||
| + | {{pdf|Peter Fischer_Sinus,_Kosinus,_Tangens.pdf|Sinus, Kosinus, Tangens}} | ||
| + | |||
| + | Hier ist ein MindMap, dass die wichtigsten Inhalte des Kapitels Trigonometrie zusammenfasst. Du kannst es dir auch ausdrucken! | ||
| + | {{pdf|Peter Fischer_Trigonometrie.pdf|MindMap Potenzen und Potenzfunktionen}} | ||
| + | |||
| + | |||
| + | <ggb_applet height="550" width="600" showMenuBar="false" showResetIcon="true" filename="Peter Fischer_Einheitskreis.ggb" /> | ||
<span style="color:#FFFFFF"><big>Leerzeile</big></span> | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
| Zeile 40: | Zeile 31: | ||
{| border="1" | {| border="1" | ||
! width="12" style="background-color:#FFD700;"| | ! width="12" style="background-color:#FFD700;"| | ||
| − | | width=" | + | | width="900" style="text-align:left" style="background-color:#FFEC8B;"| '''Aufgabe 1 [[Bild:Peter_Fischer_Taschenrechner.png|40px]]''' |
-------- | -------- | ||
Ordne den Gleichungen die richtigen Winkel zu. Bedenke, dass es stets zwei Winkel gibt. | Ordne den Gleichungen die richtigen Winkel zu. Bedenke, dass es stets zwei Winkel gibt. | ||
| Zeile 46: | Zeile 37: | ||
<div class="zuordnungs-quiz"> | <div class="zuordnungs-quiz"> | ||
| − | {| | + | {| <math>\sin \alpha=\frac{1}{2}</math> || <math>\quad \alpha=30^\circ</math> || <math>\quad \alpha=150^\circ</math> |
|- | |- | ||
| − | | <math>\sin \alpha=0,707 \quad</math> || <math>\quad \alpha=315^\circ</math> || <math>\quad \alpha=225^\circ</math> | + | | <math>\sin \alpha=-0,707 \quad</math> || <math>\quad \alpha=315^\circ</math> || <math>\quad \alpha=225^\circ</math> |
|- | |- | ||
| <math>\cos \alpha=\frac{1}{2}</math> || <math>\quad \alpha=60^\circ</math> || <math>\quad \alpha=300^\circ</math> | | <math>\cos \alpha=\frac{1}{2}</math> || <math>\quad \alpha=60^\circ</math> || <math>\quad \alpha=300^\circ</math> | ||
|- | |- | ||
| − | | <math>\cos \alpha= | + | | <math>\cos \alpha=0,866 \quad</math> || <math>\quad \alpha=30^\circ</math> || <math>\quad \alpha=330^\circ</math> |
| − | + | ||
| − | + | ||
|- | |- | ||
| <math>\tan \alpha=1 \quad</math>|| <math>\quad \alpha=45^\circ</math> || <math>\quad \alpha=135^\circ</math> | | <math>\tan \alpha=1 \quad</math>|| <math>\quad \alpha=45^\circ</math> || <math>\quad \alpha=135^\circ</math> | ||
| Zeile 64: | Zeile 53: | ||
{| border="1" | {| border="1" | ||
! width="12" style="background-color:#FFD700;"| | ! width="12" style="background-color:#FFD700;"| | ||
| − | | width=" | + | | width="900" style="text-align:left" style="background-color:#FFEC8B;"| '''Aufgabe 2 [[Bild:Peter_Fischer_Papier.png|40px]] ''' |
-------- | -------- | ||
Hier warten zwei trigonometrische Gleichungen, die mit Hilfe der Zusammenhänge gelöst werden können. | Hier warten zwei trigonometrische Gleichungen, die mit Hilfe der Zusammenhänge gelöst werden können. | ||
| + | |} | ||
| + | |||
| + | <math>\quad {\sin}^2 \alpha +2 cos \alpha =0,5</math> | ||
| + | {| | ||
| + | |[[Bild:Peter_Fischer_Tipp.png|35px|''Mori hat einen Tipp für dich'']] | ||
| + | |<popup name="Tipp"> | ||
| + | <math>\quad {\sin}^2 \alpha </math> durch <math>\quad 1-{\cos}^2 \alpha</math> ersetzen, Umformen und in die allgemeine Lösungsformel für quadratische Gleichungen einsetzen. | ||
| + | </popup> | ||
|} | |} | ||
<quiz display="simple"> | <quiz display="simple"> | ||
{ | { | ||
| type="{}" } | | type="{}" } | ||
| − | <math>\quad | + | '''Lösung:''' <math>\quad \alpha_1</math>={ 103 _7}°; <math>\quad \alpha_2</math>={ 257 _7}° (Auf ganze Zahlen gerundet!) |
| − | + | </quiz> | |
| − | + | ||
| + | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
| + | |||
<math>\quad \sin \alpha=\sqrt{3} \cdot \cos \alpha</math> | <math>\quad \sin \alpha=\sqrt{3} \cdot \cos \alpha</math> | ||
| − | <popup name="Tipp"> <math>\frac{\sin \alpha}{\cos \alpha}=\tan \alpha</math> | + | {| |
| − | Lösung: <math>\quad \alpha_1</math>={ 60 | + | |[[Bild:Peter_Fischer_Tipp.png|35px|''Mori hat einen Tipp für dich'']] |
| + | |<popup name="Tipp"> | ||
| + | <math>\frac{\sin \alpha}{\cos \alpha}=\tan \alpha</math> | ||
| + | </popup> | ||
| + | |} | ||
| + | <quiz display="simple"> | ||
| + | { | ||
| + | | type="{}" } | ||
| + | '''Lösung:''' <math>\quad \alpha_1</math>={ 60 _7}°; <math>\quad \alpha_2</math>={ 300 _7}° | ||
</quiz> | </quiz> | ||
| Zeile 83: | Zeile 90: | ||
<poem> | <poem> | ||
<span style="color:#FFFFFF"><big>Leerzeile</big></span> | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
| − | '''Weiter gehts zu [[Trigonometrische Funktionen]]''' | + | '''Weiter gehts zu [[/Trigonometrische Funktionen|Trigonometrische Funktionen]]''' |
<span style="color:#FFFFFF"><big>Leerzeile</big></span> | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
</poem> | </poem> | ||
| Zeile 89: | Zeile 96: | ||
<div style="background:#FFD700;text-align:center;color: #fff;font-weight:bold;font-size:125%;margin: 10px 5px 0px 0; padding: 4px 4px 4px 14px;">Trigonometrie</div> | <div style="background:#FFD700;text-align:center;color: #fff;font-weight:bold;font-size:125%;margin: 10px 5px 0px 0; padding: 4px 4px 4px 14px;">Trigonometrie</div> | ||
<div style="margin: 0 5px 5px 0; padding: 1em 1em 1em 1em; text-align:center; border: 1px solid :#FFD700; background-color:#f6fcfe;"> | <div style="margin: 0 5px 5px 0; padding: 1em 1em 1em 1em; text-align:center; border: 1px solid :#FFD700; background-color:#f6fcfe;"> | ||
| − | [[LERNPFAD]] | [[Trigonometrie]] | [[Trigonometrische Funktionen]] | [[Berechnungen in Dreiecken]] | [[Skalarprodukt]] | [[Exkurs: | + | [[../|LERNPFAD]] | [[../Trigonometrie|Trigonometrie]] | [[/Trigonometrische Funktionen|Trigonometrische Funktionen]] | [[/Berechnungen in Dreiecken|Berechnungen in Dreiecken]] | [[/Skalarprodukt|Skalarprodukt]] | [[/Exkurs Geometrie|Exkurs: Wichtiges zur Geometrie]] </div> |
Aktuelle Version vom 2. Juli 2017, 22:57 Uhr
| Arbeitsauftrag
Als erstes schauen wir uns an, welche Bedeutung Sinus, Cosinus und Tangens am Einheitskreis haben. Anschließend wird der Umgang mit diesen Werkzeugen zur Winkelberechnung erklärt. Klick dich durch! |
[ www.slideshare.net is not an authorized iframe site ]
Potenzfunktion
Falls die Präsentation nicht geladen werden kann, kannst du sie auch als PDF anschauen. Einfach anklicken.
![]() Sinus, Kosinus, Tangens
Sinus, Kosinus, Tangens
Hier ist ein MindMap, dass die wichtigsten Inhalte des Kapitels Trigonometrie zusammenfasst. Du kannst es dir auch ausdrucken!
![]() MindMap Potenzen und Potenzfunktionen
MindMap Potenzen und Potenzfunktionen
Leerzeile
Aufgaben
Es geht nun darum Sinus, Cosiunus un Tangens als Rechenwerkzeuge kennen zu lernen!
| Aufgabe 1 Ordne den Gleichungen die richtigen Winkel zu. Bedenke, dass es stets zwei Winkel gibt. |
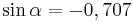 |
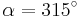 |
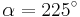
|
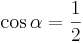 |
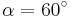 |
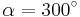
|
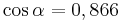 |
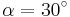 |
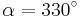
|
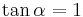 |
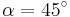 |
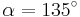
|
Leerzeile
| Aufgabe 2 Hier warten zwei trigonometrische Gleichungen, die mit Hilfe der Zusammenhänge gelöst werden können. |
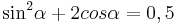
Leerzeile
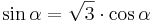
Leerzeile
Weiter gehts zu Trigonometrische Funktionen
Leerzeile
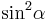 durch
durch 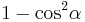 ersetzen, Umformen und in die allgemeine Lösungsformel für quadratische Gleichungen einsetzen.
ersetzen, Umformen und in die allgemeine Lösungsformel für quadratische Gleichungen einsetzen.