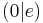Die Quadratische Funktion der Form f(x) = (x-d)² + e - Die Scheitelpunktsform: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
(Station 2 - Übungen fertig gestellt)
(Station 3 begonnen - Parameter d stellt sich vor)
Zeile 170: Zeile 170:
  
 
<br><br>
 
<br><br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
 +
 +
 +
<div align="center"><big><u>'''STATION 3: Der Parameter d stellt sich vor'''</u></big></div>
 +
 +
 +
Nachdem du jetzt Parameter e kennst, wollen wir uns nun mit dem Parameter d beschäftigen, der wie folgt in die quadratische Funktion integriert wird:
 +
 
 +
                                        '''f(x) = (x - d)²'''
 +
 +
 +
Um die Eigenschaften des Parameters d zu erlernen, bediene in der Grafik den Schieberegler d und löse im Anschluss den Lückentext.
 +
Die blaue Parabel ist abhängig vom Parameter d und die schwarz-gestrichelte Linie stellt die Normalparabel dar.
 +
Um deine Ergebnisse zu überprüfen musst du mit gehaltener linker Maustaste über das graue Feld ziehst, damit wird das Ergebnis sichtbar!! Aber nicht mogeln!
 +
 +
 +
<br>
 +
{| {{Prettytable}}
 +
|- style="background-color:#8DB6CD"
 +
| <ggb_applet height="450" width="450" showResetIcon="true" filename="VerschiebenParameterd.ggb" /> || <br>
 +
<br> !!!Bewege den Schieberegler d. Was verändert sich an der Lage der Parabel im Vergleich zur Normalparabel?
 +
<br>
 +
<br>
 +
<br>
 +
* Der Parameter d der quadratischen Funktion f(x) = (x - d)² bewirkt eine <u style="color:lightgrey;background:lightgrey">Verschiebung</u> der Normalparabel auf der <u style="color:lightgrey;background:lightgrey">x-Achse</u>. Wie schon bei der Verschiebung beim Parameter e, ist die verschobene Parabel <u style="color:lightgrey;background:lightgrey">kongruent</u> zur Normalparabel. <br>
 +
<br>
 +
* Mit Hilfe des Schiebereglers d stellt man fest, dass für positive d-Werte eine Verschiebung um <u style="color:lightgrey;background:lightgrey">d</u> Einheiten nach <u style="color:lightgrey;background:lightgrey">rechts</u> erfolgt. Ist der Wert von d <u style="color:lightgrey;background:lightgrey">negativ</u>, so wird der Graph um d Einheiten nach <u style="color:lightgrey;background:lightgrey">links</u> verschoben.
 +
<br>
 +
* Aber Achtung! Es wird ein kleines Verwirrspiel getrieben, denn für positive d-Werte lautet die Funktionsgleichung f(x) = <u style="color:lightgrey;background:lightgrey">(x - d)²</u>. Man macht leicht den Fehler und denkt positiv müsste doch (x + d)². Da jedoch die Ausgangsfunktionsgleichung f(x) = (x - d)² lautet, entsteht für positive d-Werte eine <u style="color:lightgrey;background:lightgrey">VDifferenz</u> in der Klammer. Genau andersherum verhält es sich für negative d-Werte, dort lautet die Funktionsgleichung f(x) = <u style="color:lightgrey;background:lightgrey">(x + d)²</u>.
 +
<br>
 +
* Für den Scheitelpunkt gelten die Koordinaten S <u style="color:lightgrey;background:lightgrey">(d, 0)</u>, denn der x-Wert bleibt immer <u style="color:lightgrey;background:lightgrey">Null</u>.
 +
<br>
 +
* Als Symmetrieachse ergibt sich daher die Parallelachse zur y-Achse senkrecht zur <u style="color:lightgrey;background:lightgrey">x-Achse</u>.
 +
 +
|}

Version vom 16. Juli 2009, 00:43 Uhr

Mathematik-digital Pfeil-3d.png
Lernpfad

Die Quadratische Funktion der Form f(x)=(x-d)²+ e - Die Scheitelpunktsform


In diesem Lernpfad lernst du die Scheitelpunktsform kennen! Bearbeite den unten aufgeführten Lernpfad

  • Der Parameter e stellt sich vor
  • Übungen zum Parameter e
  • Der Parameter d stellt sich vor
  • Übungen zum Parameter d
  • Zusammenführung von Parameter e und d zur Scheitelpunktsform
  • Aufgaben zur Scheitelpunktsform


Bis jetzt haben wir die Normalparabel f(x) = x² kennen gelernt. Dazu kam dann ein Parameter a als Vorfaktor, welcher die Parabel in Richtung der y-Achse gestreckt oder gestaucht hat und sie zusätzlich bei negativen Werten an der x-Achse spiegelt.

Nun wollen wir uns mit zwei weiteren Parametern beschäftigen.



STATION 1: Der Parameter e stellt sich vor


Zunächst betrachten wir den Parameter e, welcher zur Normalparabel addiert wird. Die quadratische Funktion schaut dann wie folgt aus: 

                                    f(x) = x² + e

Bearbeite das folgende Arbeitsblatt und entdecke die Eigenschaften des Parameters e!

Quadratische Funktion f(x)=x2+ e Hinweise, Aufgabe und Lückentext:

Hinweise:
* In der Grafik ist die Normalparabel schwarz-gestrichelt eingezeichnet und die von e abhängige quadratische Funktion blau
* Bediene den schwarzen Schieberegler e mit der linken Maustaste, er verändert den Wert von e
* Ziehe im Lückentext die möglichen Lösungen mit gehaltener linker Maustaste in die richtigen Felder.


Aufgabe:
Bediene den Schieberegler p. Welche Veränderungen bewirkt der Faktor e?


Lückentext! - Ordne die richtigen Begriffe zu:

Der Parameter e verschiebt die Normalparabel auf der y-Achse. Dabei bleibt die verschobene Parabel kongruent zur Normalparabel.
Ist der Parameter e positiv, so wird die Normalparabel um e Einheiten in Richtung der y-Achse nach oben verschoben.
Ist der Parameter e hingegen negativ, so wird die Normalparabel um e Einheiten in Richtung der y-Achse nach unten verschoben.
Der Scheitelpunkt befindet sich immer auf der y-Achse, genauer gesagt bei Punkt Punktfüre.jpg. Bei dieser Parabel ist die y-Achse die Symmetrieachse der Parabel.


Nuvola apps kig.png   Merke

Für die quadratische Funktion f(x)=x² + e gilt:

  • Der Graph entsteht aus der Normalparabel durch eine Verschiebung um e Einheiten auf der y-Achse → Der Graph ist kongruent zur Normalparabel
  • Für e > 0 gilt: Verschiebung nach oben, um e Einheiten in Richtung der y-Achse
  • Für e < 0 gilt: Verschiebung nach unten, um e Einheiten in Richtung der y-Achse
  • Der Scheitelpunkt liegt bei S (0\!\,|\!\,e)
  • Die y-Achse ist die Symmetrieachse


Nun folgen einige Aufgaben, um das gerade erlernte Wissen zu vertiefen.



STATION 2: Übungen zum Parameter e



1. Aufgabe: Zuordnung

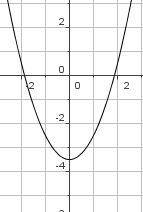
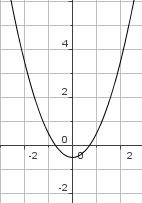
Du siehst in der Grafik 5 verschiedene quadratische Funktionen. Ermittle zu den vorgegebenen Graphen die Funktionsgleichung:


Parabele1.jpg Parabele2.jpg Parabele3.jpg Parabele4.jpg Parabele5.jpg
x2+2,5 x2+1,5 x2 x2-3,5 x2-0,5




2. Aufgabe:

Bestimme die Funktionsgleichung mit Hilfe der vorgegebenen Scheitelpunkte: 

  a) S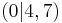 (0\!\,|\!\,4,7) 

  b) S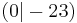 (0\!\,|\!\,-23) 

  c) S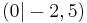 (0\!\,|\!\,-2,5) 

  d) S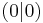 (0\!\,|\!\,0) 

  e) S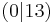 (0\!\,|\!\,13)

Lösung:


Das war bestimmt kein Problem! Man musste ja lediglich den y-Wert ablesen, da er den Wert von e angibt! 

  a)	f(x)=x² + 4,7

  b)	f(x)=x² - 23

  c)	f(x)=x² - 2,5

  d)	f(x)=x² 

  e)	f(x)=x² + 13



3. Aufgabe:

Nun hast du die Funktionsgleichung gegeben. Finde den zugehörigen Scheitelpunkt S. 

  a)	f(x)=x² + 5,2 
  
  b)	f(x)=x² - 3
  
  c)	f(x)=x² 
  
  d)	f(x)=3 + x²

Hilfe:
Falls du Probleme hast, kannst du dir ein Beispiel anzeigen lassen, aber überlege erst selbst, es ist nicht schwer!

a) S (0\!\,|\!\,5,2)

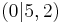
Lösung:

Der x-Wert ist immer 0, denn die Parabel wird nur nach oben oder unten verschoben. Den y-Wert kann man gut ablesen, denn er ist identisch dem Wert von e! 

  a)	S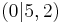 (0\!\,|\!\,5,2) 

  b)	S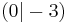 (0\!\,|\!\,-3) 

  c)	S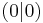 (0\!\,|\!\,0) 

  d)	S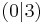 (0\!\,|\!\,3)



4. Aufgabe: Zuordnung

Die Punkte A, B, C, D, E und F liegen auf der Parabel f(x) = 2,5 + x². Ordne die fehlenden Koordinaten zu!!

A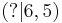(?\!\,|\!\,6,5) B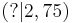(?\!\,|\!\,2,75) C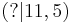(?\!\,|\!\,11,5) D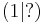(1\!\,|\!\,?) E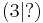(3\!\,|\!\,?) F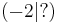(-2\!\,|\!\,?)
2 0,5 3 3,5 11,5 6,5









STATION 3: Der Parameter d stellt sich vor


Nachdem du jetzt Parameter e kennst, wollen wir uns nun mit dem Parameter d beschäftigen, der wie folgt in die quadratische Funktion integriert wird: 

                                       f(x) = (x - d)²


Um die Eigenschaften des Parameters d zu erlernen, bediene in der Grafik den Schieberegler d und löse im Anschluss den Lückentext. Die blaue Parabel ist abhängig vom Parameter d und die schwarz-gestrichelte Linie stellt die Normalparabel dar. Um deine Ergebnisse zu überprüfen musst du mit gehaltener linker Maustaste über das graue Feld ziehst, damit wird das Ergebnis sichtbar!! Aber nicht mogeln!





 !!!Bewege den Schieberegler d. Was verändert sich an der Lage der Parabel im Vergleich zur Normalparabel?


  • Der Parameter d der quadratischen Funktion f(x) = (x - d)² bewirkt eine Verschiebung der Normalparabel auf der x-Achse. Wie schon bei der Verschiebung beim Parameter e, ist die verschobene Parabel kongruent zur Normalparabel.


  • Mit Hilfe des Schiebereglers d stellt man fest, dass für positive d-Werte eine Verschiebung um d Einheiten nach rechts erfolgt. Ist der Wert von d negativ, so wird der Graph um d Einheiten nach links verschoben.


  • Aber Achtung! Es wird ein kleines Verwirrspiel getrieben, denn für positive d-Werte lautet die Funktionsgleichung f(x) = (x - d)². Man macht leicht den Fehler und denkt positiv müsste doch (x + d)². Da jedoch die Ausgangsfunktionsgleichung f(x) = (x - d)² lautet, entsteht für positive d-Werte eine VDifferenz in der Klammer. Genau andersherum verhält es sich für negative d-Werte, dort lautet die Funktionsgleichung f(x) = (x + d)².


  • Für den Scheitelpunkt gelten die Koordinaten S (d, 0), denn der x-Wert bleibt immer Null.


  • Als Symmetrieachse ergibt sich daher die Parallelachse zur y-Achse senkrecht zur x-Achse.
Von „http://dmuw.zum.de/index.php?title=Lernpfade/Quadratische_Funktionen/Die_Quadratische_Funktion_der_Form_f(x)_%3D_(x-d)²_%2B_e_-_Die_Scheitelpunktsform&oldid=3565“