The tidiness of elementary mathematics: Unterschied zwischen den Versionen
Aus DMUW-Wiki
| Zeile 4: | Zeile 4: | ||
\int x^{-1}\mathrm{d}x = \int \frac{1}{x}\mathrm{d}x = \ln(x).</math> | \int x^{-1}\mathrm{d}x = \int \frac{1}{x}\mathrm{d}x = \ln(x).</math> | ||
| − | Our expectation is that these two formulae should be reconciled. Indeed, if we let <math>k</math> approach <math>-1</math> in the first we should end up with the second, but that fails to happen. For each <math>x</math>, <math>\lim_{k\rightarrow -1} \frac{x^{k+1}}{k+1} </math> is undefined. | + | Our expectation is that these two formulae should be reconciled. Indeed, if we let <math>k</math> approach <math>-1</math> in the first we should end up with the second, but that fails to happen. For each <math>x</math>, <math>\lim_{k\rightarrow -1} \frac{x^{k+1}}{k+1} </math> is undefined. |
| + | |||
| + | This vingette explores this issue. | ||
== Main article == | == Main article == | ||
| + | |||
| + | == Applets == | ||
Version vom 9. November 2011, 00:19 Uhr
We all expect a certain tidiness to mathematics, and for many this provides a gratifying aesthetic pleasure. However, there are some wrinkles. One of these arises in the integral of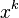 
. Calculus provides us with the formula 
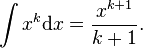However, this equation is only correct for 
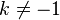. If we try to take 
the right hand side is meaningless because we have a zero on the denominator of the fraction, i.e. 
. But in this case a separate argument gives the answer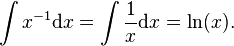 
Our expectation is that these two formulae should be reconciled. Indeed, if we let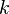 
approach 
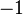in the first we should end up with the second, but that fails to happen. For each 
, 
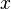is undefined.
This vingette explores this issue.
