The tidiness of elementary mathematics
We all expect a certain { tidiness} to mathematics, and for many this provides a gratifying aesthetic pleasure. However, there are some wrinkles. One of these arises in the integral of 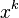 . Calculus provides us with the formula Fehler beim Parsen(Unbekannte Funktion „\label“): \label{eq:int_xk} \int x^k\mathrm{d}x = \frac{x^{k+1}}{k+1}.
. Calculus provides us with the formula Fehler beim Parsen(Unbekannte Funktion „\label“): \label{eq:int_xk} \int x^k\mathrm{d}x = \frac{x^{k+1}}{k+1}.
However, this equation is only correct for. If we try to take
the right hand side is meaningless because we have a zero on the denominator of the fraction, i.e.
. But in this case a separate argument gives the answer Fehler beim Parsen(Unbekannte Funktion „\label“): \label{eq:int_log} \int x^{-1}\mathrm{d}x = \int \frac{1}{x}\mathrm{d}x = \ln(x).%\ln(|x|). Our expectation is that these two formulae should be reconciled. Indeed, if we let
approach
in the first we should end up with the second, but that fails to happen. For each
,
is undefined. You can try this on the graph below.
This is particularly problematic when we attempt to automate knowledge, that is when we seek to devise a { computer algebra system} which will symbolically manipulate expressions. If we want to integrate 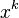 with respect to
with respect to  we certainly have two choices
we certainly have two choices
- Ignore the special case
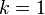 .
.
- Ask the user if
 .
.
Both of these approaches are problematic.  is only one point out of an infinity of other values for
is only one point out of an infinity of other values for 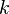 . However, in mathematics such exceptional cases occur rather more often than you might expect if you just stuck a pin in the number line, or even if you chose an integer
. However, in mathematics such exceptional cases occur rather more often than you might expect if you just stuck a pin in the number line, or even if you chose an integer 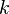 at random. Asking the user can also be problematic as they many not yet know the value of
at random. Asking the user can also be problematic as they many not yet know the value of 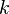 , or the integral might occur deep within some other function and the user may have no idea what the question is asking! Automatically using the formula might result in an error creeping into a much longer calculation. Mistakes like this are very hard to track down and can be serious.
, or the integral might occur deep within some other function and the user may have no idea what the question is asking! Automatically using the formula might result in an error creeping into a much longer calculation. Mistakes like this are very hard to track down and can be serious.
What we would really like is a formula that works for all 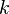 . Here we are going to consider the comment in that really, at a symbolic level, the answer to
. Here we are going to consider the comment in that really, at a symbolic level, the answer to 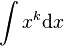 might better be written as Fehler beim Parsen(Unbekannte Funktion „\label“): \label{eq:int_xk2} \int x^k\mathrm{d}x = \frac{x^{k+1}-1}{k+1}+c.
might better be written as Fehler beim Parsen(Unbekannte Funktion „\label“): \label{eq:int_xk2} \int x^k\mathrm{d}x = \frac{x^{k+1}-1}{k+1}+c.
First consider the (easy) case 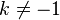 . If we fix
. If we fix 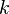 and differentiate then we obtain
and differentiate then we obtain 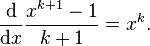 So
So  is an anti-derivative of
is an anti-derivative of 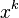 . Really we have chosen a slightly different constant of integration.
. Really we have chosen a slightly different constant of integration.
Whereas we originally had the form 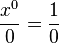 , the new formula gives
, the new formula gives 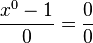 . To understand what is going on we need to look at this expression for
. To understand what is going on we need to look at this expression for 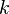 close to
close to 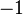 and take a { limit}, i.e.
and take a { limit}, i.e. 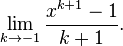 If we can make sense of this limit, then we will define the value of the expression at
If we can make sense of this limit, then we will define the value of the expression at  by the value of the limit, thus removing the exceptional case in a meaningful way. This sort of thing is a standard mathematician’s move.
by the value of the limit, thus removing the exceptional case in a meaningful way. This sort of thing is a standard mathematician’s move.

