Wiederholung-1: Unterschied zwischen den Versionen
| Zeile 155: | Zeile 155: | ||
}} | }} | ||
}} | }} | ||
| + | Ich habe hier ein paar Fragen an dich um zu sehen, ob du wirklich alles verstanden hast, was wir bisher zusammen gemacht haben. | ||
| + | <br /><br /> | ||
| + | <small>Wenn du dir nicht sicher bist, überprüfe die Dreiecke mit Hilfe des GeoGebra-Applets unter der Tabelle.</small> | ||
| + | |||
| + | <quiz> | ||
| + | { Kann man das Dreieck mit folgenden Maßen konstruieren? | ||
| + | | typ="()" } | ||
| + | | Ja | Nein | | ||
| + | -+ a=7,5 cm, b=3,0cm, c=3,5cm, γ=40° | ||
| + | +- | ||
| + | -- | ||
| + | </quiz> | ||
| + | |||
| + | <ggb_applet height="600" width="800" showResetIcon="true" filename="KS_1.Lernpfad_Abschlussaufgabe" /> | ||
Version vom 17. Januar 2010, 20:10 Uhr
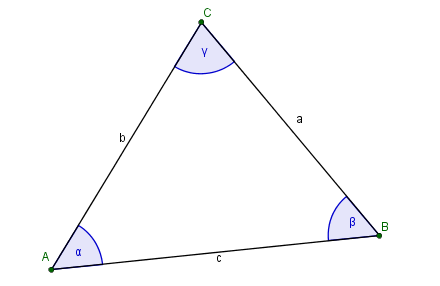
Du hast bereits gelernt, dass ich -wie mein Name ja auch sagt- drei Eckpunkte und drei Seiten habe. Leider ist hier die Beschriftung etwas durcheinander geraten. Kanst du meine Seiten bitte so beschriften, wie du es gelernt hast?
Klicke dazu die Punkte an und ziehe sie an die richtige Ecke im Dreieck. Prüfe anschließend dein Ergebnis.
ACHTUNG:
Die Ecke, die der Seite a gegenüberliegt heißt A,
die Ecke, die der Seite b gegenüberliegt heißt B,
die Ecke, die der Seite c gegenüberliegt heißt C.
Danke, so schaut das Ganze doch schon viel ordentlicher aus.
Die Winkel werden normalerweise mit den Buchstaben α, β und γ bezeichnet.
Aus welcher Sprache stammen sie?
Kannst du diese Buchstaben auch noch den richtigen Winkeln zuordnen? Ziehe dazu die passenden Felder in die grünen Lücken hinter den Buchstaben A, B und C.
| Der Winkel an der Ecke ___ | heißt ___ | und wird gebildet von den Seiten ___ |
| A | ||
| B | ||
| C |
αb und ca und bβa und cγ
Das war ja bisher noch nicht so schwer.
Zur Erinnerung findest du hier nochmal ein Bild von einem Dreieck mit den üblichen Bezeichnungen der Ecken, Seiten und Winkel. [Anzeigen]
Übertrage die Bezeichnungen in das Dreieck auf deinem Laufzettel zum 1.Lernpfad!
Je nach Größe der Winkel und Länge der Seiten kann ich verschiedene Formen annehmen. Kennst du sie noch alle?
Zuordnung
Ordne die Satzteile den Begriffen zu, so dass die richtigen Definitionen entstehen.
gleichseitiges Dreieck:
rechtwinkliges Dreieck:
gleichschenkliges Dreieck:
stumpfwinkliges Dreieck:
spitzwinkliges Dreieck:
zwei Seitenein Winkel >ein Winkel beträgtalle drei Winkel sind gleich groß (60°)(zwei Schenkel) sind gleich lang(größer als) 90°(kleiner als) 90°sind gleich langalle drei Seitenalle drei Winkel <genau 90°
Wenn du die Satzteile richtig zugeordnet hast, klicke hier um die Definitionen anzuzeigen:
[Anzeigen]
Übertrage die Definitionen auf deinen Laufzettel zum 1.Lernpfad!
Sehr schön! Jetzt haben wir die verschiedenen Formen gesehen und definiert. Findest du im memo-quiz die richtigen Paare?
rechtwinkliges Dreieck 
gleichseitiges Dreieck 
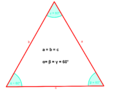gleichschenkliges Dreieck stumpfwinkliges Dreieck spitzwinkliges Dreieck
Das war nicht so schwer. Findest du auch die richtigen Dreiersets?
spitzwinkliges Dreieck Zwei Seiten sind gleich lang.
Alle drei Seiten sind gleich lang und alle drei Winkel gleich groß (60°).
Ein Winkel > (ist größer als) 90°.
rechtwinkliges Dreieck Ein Winkel < (ist kleiner als) 90°.
gleichschenkliges Dreieck gleichseitiges Dreieck stumpfwinkliges Dreieck Ein Winkel beträgt genau 90°.
Mit den Dreiecken kenst du dich ja schon richtig gut aus!
Klicke auf den Punkt A in Dreieck und verschiebe ihn. Schau dir dabei die Seitenlängen und Winkelgrößen an. Was fällt dir auf?
Auf deinem Laufzettel findest du vier Tabellen.
a) Verschiebe den Punkt A so, dass du ein spitzwinkliges Dreieck erhälst. Ließ die Werte ab und fülle damit auf deinem Laufzettel die erste Tabelle aus.
b) Verschiebe den Punkt A erneut, so dass du ein neues spitzwinkliges Dreieck erhälst. Ließ die Werte ab und fülle die zweite Tabelle aus.
c) Verschiebe den Punkt A so, dass du ein stumpfwinkliges Dreieck erhälst. Ließ die Werte ab und fülle die dritte Tabelle auf deinem Laufzettel aus.
d) Verschiebe den Punkt A wieder, so dass du ein neues stumpfwinkliges Dreieck erhälst. Ließ die Werte ab und fülle die vierte Tabelle auf deinem Laufzettel aus.
Wenn wir uns jetzt die Tabellen anschauen, dann sehen wir, dass der größeren (esite) immer der größere (nliewk) gegenüberliegt.
Übertrage den Merksatz auf deinen Laufzettel
Klicke hier, um den Merksatz anzuzeigen:
[Anzeigen]
Klicke die Punkte A, B und C an und verschiebe sie.
Vergleiche die Längen der Dreiecksseiten mit der Summe der beiden anderen Seitenlängen.
Was stellt du fest?
Wenn du eine Idee hast klicke auf [Anzeigen] und sieh nach, ob du richtig gelegen hast.
Schreibe den Merksatz auf deinen Laufzettel.
[Anzeigen]
Ich habe hier ein paar Fragen an dich um zu sehen, ob du wirklich alles verstanden hast, was wir bisher zusammen gemacht haben.
Wenn du dir nicht sicher bist, überprüfe die Dreiecke mit Hilfe des GeoGebra-Applets unter der Tabelle.
