Lineare Gleichungssysteme grafisch lösen/Station 4: Unterschied zwischen den Versionen
| Zeile 48: | Zeile 48: | ||
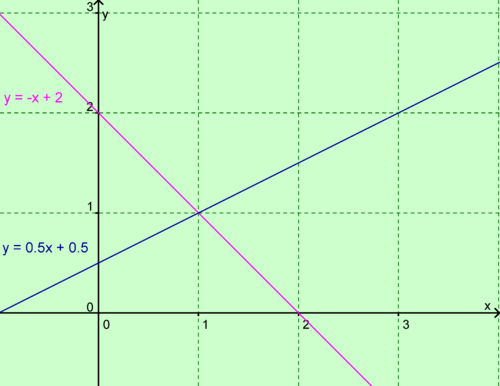
Die Geraden haben '''einen''' Schnittpunkt.<br> | Die Geraden haben '''einen''' Schnittpunkt.<br> | ||
Die Steigung der beiden Geraden ist '''unterschiedlich'''.<br> | Die Steigung der beiden Geraden ist '''unterschiedlich'''.<br> | ||
| − | Die Lösungsmenge dieses Beispiels lautet L = { ( 1 | 1 ) }. | + | Die Lösungsmenge dieses Beispiels lautet L = { ( 1 | 1 ) }.<br> |
| + | Es gibt also genau ein Zahlenpaar, dass auf beiden Geraden liegt. | ||
</div> | </div> | ||
| Zeile 63: | Zeile 64: | ||
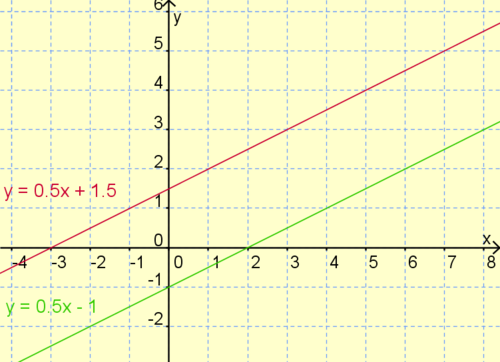
Die Steigung der beiden Geraden ist '''gleich'''.<br> | Die Steigung der beiden Geraden ist '''gleich'''.<br> | ||
Sie sind also '''parallel'''<br> | Sie sind also '''parallel'''<br> | ||
| − | Die Lösungsmenge lautet L = { }. | + | Die Lösungsmenge lautet L = { }.<br> |
| + | Es gibt also kein Zahlenpaar, dass auf beiden Geraden gleichzeitig liegt. | ||
</div> | </div> | ||
| Zeile 77: | Zeile 79: | ||
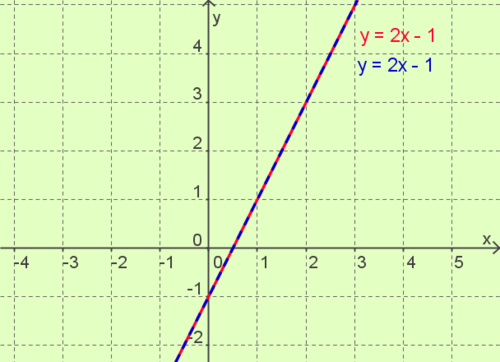
Die Geraden sind '''identisch'''.<br> | Die Geraden sind '''identisch'''.<br> | ||
Ihre Steigung und ihre y - Achsenabschnitte sind '''gleich'''.<br> | Ihre Steigung und ihre y - Achsenabschnitte sind '''gleich'''.<br> | ||
| − | Die Lösungsmenge des Beispiels lautet L = { ( x | y ) / y = 2x - 1 }. | + | Die Lösungsmenge des Beispiels lautet L = { ( x | y ) / y = 2x - 1 }.<br> |
Also sind alle Zahlenpaare, die auf dieser Geraden liegen, Lösungen des Linearen Gleichungssystems. | Also sind alle Zahlenpaare, die auf dieser Geraden liegen, Lösungen des Linearen Gleichungssystems. | ||
Version vom 19. Januar 2010, 18:28 Uhr
Station 4
Hier sind wieder zwei Geraden f (x) und g (x) dargestellt.
Mit den Schiebereglern kannst du die Steigung ( m ) und den y- Achsenabschnitt ( t ) der Geraden verändern.
Beantworte die Fragen durch Ausprobieren im obigen Koordinatensystem!
1. Haben die Geraden immer einen Schnittpunkt? (!Ja) (Nein)
2. Kannst du die Geraden so verändern, dass Sie keinen Schnittpunkt haben. (Ja) (!Nein)
3. Gibt es auch eine Möglichkeit, dass die Geraden 2 Schnittpunkte haben? (!Ja) (Nein)
4. Oder kannst du Sie so verändern, dass es unendlich viele gemeinsame Punkte gibt? (Ja) (!Nein)
Vergleiche auch die Funktionswerte in der Tabelle und die Funktionsgleichungen der beiden Geraden miteinander!
In den folgenden Zeichungen sind verschiedene Lineare Gleichungssyteme grafisch dargestellt.
Versuche die nebenstehenden Lückentexte auszufüllen.
Was fällt dir auf?
 |
Die Geraden haben einen Schnittpunkt. |
 |
Die Geraden haben keinen Schnittpunkt. |
 |
Die Geraden sind identisch. |
Versuche nun die folgende Frage zu beantworten! 
Welche Fälle können auftreten? (Das Lineare Gleichungssystem ist eindeutig lösbar, d.h. eine Lösung) (Das Lineare Gleichungssystem ist unerfüllbar, d.h. keine Lösung) (Das Lineare Gleichungssystem hat unendlich viele Lösungen) (!Das Lineare Gleichungssystem hat 2 Lösungen)
