SSS-Satz-2: Unterschied zwischen den Versionen
Aus DMUW-Wiki
K |
K |
||
| Zeile 1: | Zeile 1: | ||
| + | <div style="border: 2px solid #0000ee; background-color:#ffffff; padding:7px;"> | ||
| + | {| class="wikitable" | ||
| + | |- | ||
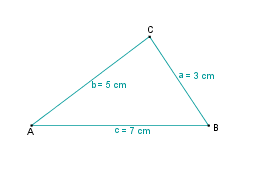
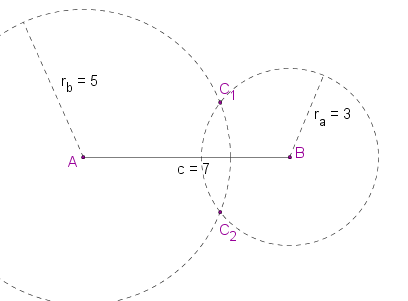
| + | | [[Bild:KS_Dreieck2.JPG ]] || Wie konstruiert man ein Dreieck, von dem alle drei Seitenlängen gegeben sind? | ||
| + | |} | ||
| + | Wir wollen ein Dreieck konstruieren, von dem die Seitenlängen a = 3 cm, b = 5 cm und c = 7 cm gegeben sind.<br /> | ||
| + | <quiz display="simple"> | ||
| + | {Als Erstes müssen wir überprüfen, ob das Dreieck mit diesen Maßen überhaupt konstruierbar ist. <br />Dies macht man hier mit der __________. } | ||
| + | - Seiten-Winkel-Beziehung | ||
| + | + Dreiecksungleichung | ||
| + | </quiz> | ||
| + | <br /> | ||
| + | <quiz> | ||
| + | { Das bedeutet, man überprüft ob die Summe von zwei Seitenlängen stets größer ist als die Länge der dritten Seite: <br /><small>(a = 7 cm, b = 5 cm und c = 3 cm)</small> | ||
| + | | type="{}" } | ||
| + | a + b > c, also 3 cm + 5 cm = { 8 } cm > 7 cm<br /> | ||
| + | b + c > a, also 5 cm + 7 cm = { 12 } cm > 3 cm<br /> | ||
| + | c + a > b, also 7 cm + 3 cm = { 10 } cm > 5 cm<br /> | ||
| + | </quiz> | ||
| + | </div> | ||
| + | |||
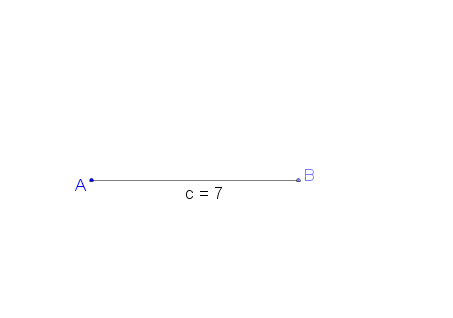
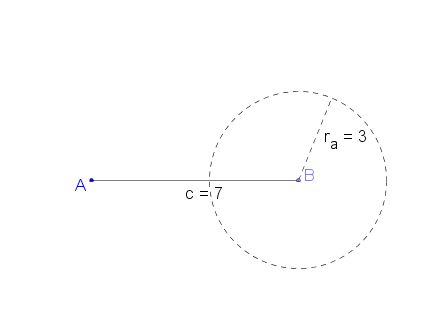
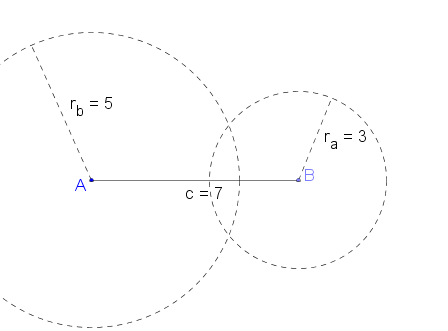
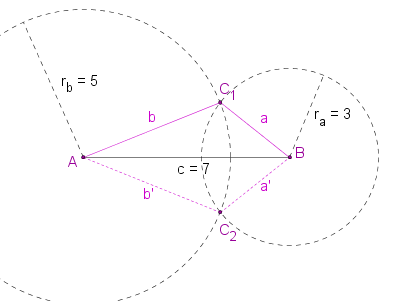
[[Bild:Dreieck.png]] Wir wissen jetzt also, dass das Dreieck mit den Seitenlängen a = 3 cm, b = 5 cm und c = 7 cm konstruierbar ist!<br /> | [[Bild:Dreieck.png]] Wir wissen jetzt also, dass das Dreieck mit den Seitenlängen a = 3 cm, b = 5 cm und c = 7 cm konstruierbar ist!<br /> | ||
<br /> | <br /> | ||
Version vom 19. Februar 2010, 14:49 Uhr
 |
Wie konstruiert man ein Dreieck, von dem alle drei Seitenlängen gegeben sind? |
Wir wollen ein Dreieck konstruieren, von dem die Seitenlängen a = 3 cm, b = 5 cm und c = 7 cm gegeben sind.
 Wir wissen jetzt also, dass das Dreieck mit den Seitenlängen a = 3 cm, b = 5 cm und c = 7 cm konstruierbar ist!
Wir wissen jetzt also, dass das Dreieck mit den Seitenlängen a = 3 cm, b = 5 cm und c = 7 cm konstruierbar ist!
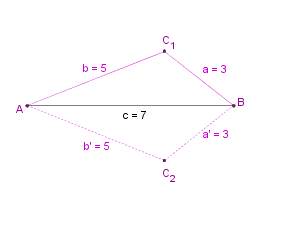
Du glaubst mir nicht, dass die Dreiecke kongruent sind? Dann schau selbst:
Zur Erinnerung: Wenn man zwei Dreiecke durch Achsenspiegelung aufeinander abbilden kann sagt man, die Dreiecke sind kongruent.
30px Merke
SSS-Satz |
|
Übertrage den Satz auf deinen Laufzettel! |
 Wenn du den Satz abgeschrieben hast, gibt es hier eine Aufgabe dazu.
Wenn du den Satz abgeschrieben hast, gibt es hier eine Aufgabe dazu.