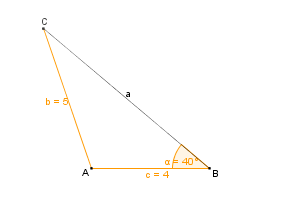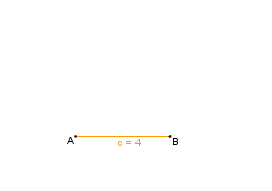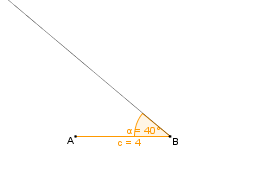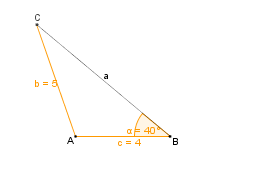SSW g-Satz-1: Unterschied zwischen den Versionen
K |
K |
||
| Zeile 16: | Zeile 16: | ||
| Um das Dreieck zu konstruieren fertigen wir zunächst eine Skizze an. Dazu zeichnen wir ein beliebiges Dreieck und markieren alle gegebenen Größen farbig. || [[Bild:KS_Planfigur_SsW.png]] | | Um das Dreieck zu konstruieren fertigen wir zunächst eine Skizze an. Dazu zeichnen wir ein beliebiges Dreieck und markieren alle gegebenen Größen farbig. || [[Bild:KS_Planfigur_SsW.png]] | ||
|- | |- | ||
| − | | Wir beginnen mit der | + | | Wir beginnen mit der '''kleineren''' der gegebenen Seiten c = 4 cm. <br /> <small>''Der Gegenwinkel der größeren Seite ist gegeben und liegt somit an der kürzeren Seite an.''</small> || [[Bild:KS_Schritt1_SsW.png]] |
|- | |- | ||
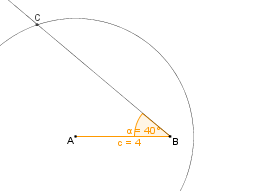
| Am Punkt B tragen wir den Winkel <math>\beta</math><math>=</math>40° ''im Uhrzeigersinn'' ab. || [[Bild:KS_Schritt2_SsW.png]] | | Am Punkt B tragen wir den Winkel <math>\beta</math><math>=</math>40° ''im Uhrzeigersinn'' ab. || [[Bild:KS_Schritt2_SsW.png]] | ||
Version vom 19. Februar 2010, 21:59 Uhr
 |
Wie konstruiert man ein Dreieck, von dem zwei Seitenlängen und das Maß des Gegenwinkels der größeren Seite gegeben sind? |
Wir wollen ein Dreieck konstruieren, von dem die Seitenlängen b = 5 cm und c = 4 cm,
sowie der Gegenwinkel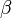 
40° gegeben sind.
Da von dem Dreieck zwei Seitenlängen und der Gegenwinkel der größeren Seite gegeben sind,
müssen wir nicht nachprüfen ob das Dreieck überhaupt konstruierbar ist!
| Um das Dreieck zu konstruieren fertigen wir zunächst eine Skizze an. Dazu zeichnen wir ein beliebiges Dreieck und markieren alle gegebenen Größen farbig. | 
|
| Wir beginnen mit der kleineren der gegebenen Seiten c = 4 cm. Der Gegenwinkel der größeren Seite ist gegeben und liegt somit an der kürzeren Seite an. |
|
| Am Punkt B tragen wir den Winkel 40° im Uhrzeigersinn ab. |
|
| Um den Punkt A zeichnen wir einen Kreis mit Radius b = 5 cm. | 
|
| Der Kreis schneidet die Halbgerade des Winkels im Punkt C. | 
|
| Wir verbinden die Punkte B und C sowie A und C und erhalten dadurch ein eindeutig festgelegtes Dreieck. | 
|
 Merke
SSWg-Satz |
Aufgabe
Übertrage den Satz auf deinen Laufzettel! |
Wenn du den Satz abgeschrieben hast, gibt es hier eine Aufgabe dazu.
