Einstieg: Unterschied zwischen den Versionen
| (13 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
__NOTOC__ | __NOTOC__ | ||
| − | <div style="margin:0; margin-right:4px; margin-left:0px; border:2px solid #f4f0e4; padding: 0em 0em 0em 1em; background-color:#f4f0e4;">[[../Einstieg|1. Fußball-WM 2006 - Wasserverbrauch]] | [[../Quadratische Funktionen|2. Quadratische Funktionen und Klippenspringen]] | [[../Übungen zu a|3. Übungen]] | [[../Quadratische Funktionen und der Parameter c|4. Quadratische Funktionen und Volleyball]] | [[../Quadratische Funktionen und der Parameter b|5. Quadratische Funktionen und Fußball]] | [[../Quadratische Funktionen und die Scheitelform|Quadratische Funktionen und Basketball]] | [[../Endspurt|Endspurt]] | + | <div style="margin:0; margin-right:4px; margin-left:0px; border:2px solid #f4f0e4; padding: 0em 0em 0em 1em; background-color:#f4f0e4;">[[../Einstieg|1. Fußball-WM 2006 - Wasserverbrauch]] | [[../Quadratische Funktionen|2. Quadratische Funktionen und Klippenspringen]] | [[../Übungen zu a|3. Übungen]] | [[../Quadratische Funktionen und der Parameter c|4. Quadratische Funktionen und Volleyball]] | [[../Quadratische Funktionen und der Parameter b|5. Quadratische Funktionen und Fußball]] | [[../Quadratische Funktionen und die Scheitelform|6. Quadratische Funktionen und Basketball]] | [[../Endspurt|7. Endspurt]] |
</div> | </div> | ||
| + | |||
<br\> | <br\> | ||
==Fußball-Weltmeisterschaft 2006 - Wasserverbrauch== | ==Fußball-Weltmeisterschaft 2006 - Wasserverbrauch== | ||
| − | Während der Fußball-Weltmeisterschaft 2006 konnten die Wasserversorger während der Spiele eine interessante Entdeckung machen.<br\>Die WVV (Würzburger Versorgungs- und Verkehrs-GmbH) hat im Versorgungsgebiet Würzburg-Heuchelhof während des Halbfinalspiels zwischen Deutschland und Italien folgende Aufzeichnungen gemacht. Aber sieh dir das selbst einmal an | + | Während der Fußball-Weltmeisterschaft 2006 konnten die Wasserversorger während der Spiele eine interessante Entdeckung machen.<br\>Die WVV (Würzburger Versorgungs- und Verkehrs-GmbH) hat im Versorgungsgebiet Würzburg-Heuchelhof während des Halbfinalspiels zwischen Deutschland und Italien folgende Aufzeichnungen gemacht. Aber sieh dir das selbst einmal an!<br\> |
| + | An der x-Achse kannst du den Zeitverlauf ablesen und an der y-Achse den Wasserverbrauch in Litern pro Sekunde. Als Hilfe ist der Spielbeginn, die Halbzeitpause und das Ende der regulären Spielzeit angezeigt. | ||
| − | Wie lässt sich der Verlauf | + | Wie lässt sich der Verlauf des Graphen erklären? |
| + | [[Bild:Laufzettel.png|50px]] Notiere deine Vermutung auf dem Laufzettel! | ||
| Zeile 37: | Zeile 40: | ||
===Aufgabe 2=== | ===Aufgabe 2=== | ||
| − | Hast du die Graphik vorliegen? Dann kannst du jetzt durch Ablesen | + | Hast du die Graphik vorliegen? Dann kannst du jetzt durch Ablesen am Funktionsgraph diese Aufgabe lösen. |
<quiz display="simple"> | <quiz display="simple"> | ||
| Zeile 50: | Zeile 53: | ||
</div> | </div> | ||
<br\> | <br\> | ||
| + | <br\> | ||
| + | [[Bild:Laufzettel.png|50px]] Bewerte die Aufgaben auf deinem Laufzettel, bevor du weitermachst! | ||
<br\> | <br\> | ||
<br\> | <br\> | ||
| Zeile 55: | Zeile 60: | ||
===Rückblick=== | ===Rückblick=== | ||
| − | + | Der Graph, den wir gemeinsam entwickelt haben, gehört zu den Graphen der '''Funktionen'''. <br\>Du kennst bereits '''lineare Funktionen'''. Dein Wissen dazu kannst du in dem Lückentext überprüfen und wiederholen. | |
<br/> | <br/> | ||
<br\> | <br\> | ||
| Zeile 65: | Zeile 70: | ||
<div class="schuettel-quiz"> | <div class="schuettel-quiz"> | ||
| − | Den Graph einer linearen Funktion nennt man '''Gerade'''. Ihr allgemeine '''Gleichung''' ist y=mx+t und wird auch als Normalform bezeichnet. | + | Den Graph einer linearen Funktion nennt man '''Gerade'''. Ihr allgemeine '''Gleichung''' ist y=mx+t und wird auch als Normalform bezeichnet. Der Parameter t gibt den '''Schnittpunkt''' mit der y-Achse an. Man sagt auch y-Achsenabschnitt der Geraden, also die Verschiebung auf der y-Achse nach '''oben''' oder unten. Am Parameter m kann man die '''Steigung''' der Geraden ablesen. |
</div> | </div> | ||
| Zeile 82: | Zeile 87: | ||
{|border="0" cellspacing="0" cellpadding="4" | {|border="0" cellspacing="0" cellpadding="4" | ||
| − | |align = "left" width="450"|Welche Unterschiede | + | |align = "left" width="450"|Wir betrachten den blauen Graph. Welche Unterschiede kannst du zum roten Graphen erkennen? |
Kreuze jeweils die richtige Anwort an. | Kreuze jeweils die richtige Anwort an. | ||
<quiz display="simple"> | <quiz display="simple"> | ||
| − | { | + | {Der blaue Graph zeigt} |
- eine Gerade. | - eine Gerade. | ||
+ keine Gerade. | + keine Gerade. | ||
| − | {Im Gegensatz | + | {Im Gegensatz zum Graph der linearen Funktion kann man} |
- keine Achsensymmetrie erkennen. | - keine Achsensymmetrie erkennen. | ||
+ eine Achsensymmetrie erkennen. | + eine Achsensymmetrie erkennen. | ||
| − | {Außerdem hat | + | {Außerdem hat er hier} |
+ einen höchsten Wert. | + einen höchsten Wert. | ||
- keinen höchsten Wert. | - keinen höchsten Wert. | ||
| Zeile 106: | Zeile 111: | ||
<br> | <br> | ||
| − | + | <br\> | |
| + | [[Bild:Laufzettel.png|50px]] Bewerte die Aufgaben auf deinem Laufzettel, bevor du weitermachst! | ||
| + | <br\> | ||
| − | Legen wir los! <div algin="left">[[../Quadratische Funktionen|<math>\Rightarrow</math> Weiter zum nächsten Kapitel]]</div> | + | Jetzt wollen wir unsere Funktion endlich benennen. Sie gehört zu den <big>'''quadratischen Funktionen'''</big>. Mit diesen Funktionen werden wir uns in den nächsten Stunden beschäftigen. Dabei lernst du bestimmte Merkmale der quadratischen Funktion und ihre Handhabung. |
| − | <br> | + | <br\> |
| + | <br\> | ||
| + | <big>Legen wir los! | ||
| + | <br\> | ||
| + | <div algin="left">[[../Quadratische Funktionen|<math>\Rightarrow</math> Weiter zum nächsten Kapitel]]</div> | ||
| + | <br></big> | ||
| + | <br\> | ||
<div align="left">[[../|<math>\Leftarrow</math> Zurück zur Übersicht]]</div> | <div align="left">[[../|<math>\Leftarrow</math> Zurück zur Übersicht]]</div> | ||
Aktuelle Version vom 23. Februar 2010, 23:42 Uhr
Fußball-Weltmeisterschaft 2006 - Wasserverbrauch
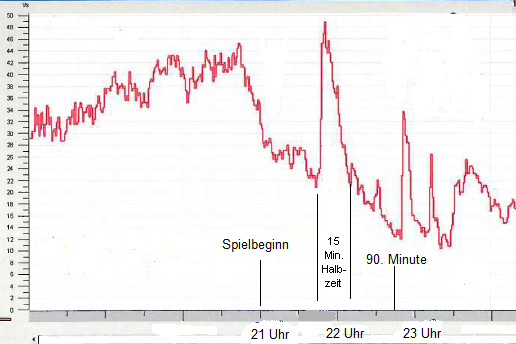
Während der Fußball-Weltmeisterschaft 2006 konnten die Wasserversorger während der Spiele eine interessante Entdeckung machen.
Die WVV (Würzburger Versorgungs- und Verkehrs-GmbH) hat im Versorgungsgebiet Würzburg-Heuchelhof während des Halbfinalspiels zwischen Deutschland und Italien folgende Aufzeichnungen gemacht. Aber sieh dir das selbst einmal an!
An der x-Achse kannst du den Zeitverlauf ablesen und an der y-Achse den Wasserverbrauch in Litern pro Sekunde. Als Hilfe ist der Spielbeginn, die Halbzeitpause und das Ende der regulären Spielzeit angezeigt.
Wie lässt sich der Verlauf des Graphen erklären?
Notiere deine Vermutung auf dem Laufzettel!
Bevor wir auf die Lösung der Frage eingehen, richten wir unser Augenmerk auf die Halbzeitpause.
Halbzeitpause
Kleine Hilfen erleichtern uns die Arbeit:
Wir arbeiten mit etwas vereinfachten Daten, die sich jedoch auf die Graphik oben beziehen. Ebenso gleichen wir die Koordinaten-Achsen einander an, indem wir die y-Werte in Hektolitern und die x-Achse in Minuten angeben. Zur Erinnerung: 1 Hektoliter = 100 Liter.
Aufgabe 1
Aufgabe 2
Hast du die Graphik vorliegen? Dann kannst du jetzt durch Ablesen am Funktionsgraph diese Aufgabe lösen.
.
Bewerte die Aufgaben auf deinem Laufzettel, bevor du weitermachst!
Rückblick
Der Graph, den wir gemeinsam entwickelt haben, gehört zu den Graphen der Funktionen.
Du kennst bereits lineare Funktionen. Dein Wissen dazu kannst du in dem Lückentext überprüfen und wiederholen.
Aufgabe 3
In dem Lückentext sind die gesuchten Wörter bereits angegeben, allerdings in verdrehter Form. Durch die richtige Buchstabenordnung erhälst du das Lösungswort für die jeweilige Lücke. Beachte bitte auch die Rechtschreibung. Viel Erfolg beim Lösen!
Den Graph einer linearen Funktion nennt man Gerade. Ihr allgemeine Gleichung ist y=mx+t und wird auch als Normalform bezeichnet. Der Parameter t gibt den Schnittpunkt mit der y-Achse an. Man sagt auch y-Achsenabschnitt der Geraden, also die Verschiebung auf der y-Achse nach oben oder unten. Am Parameter m kann man die Steigung der Geraden ablesen.
Konntest du zu allen Wörtern die richtige Lösung finden? Super!
Dann bist du jetzt wieder fit im Bereich der linearen Funktionen und wir können einen Schritt weitergehen.
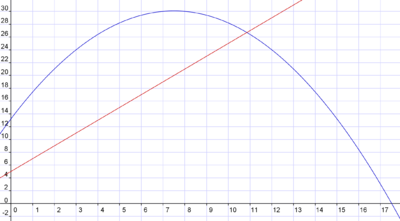
Vergleichen wir nun den Graphen der linearen Funktion mit dem unserer Halbzeitpausen-Funktion.
Aufgabe 4
| Wir betrachten den blauen Graph. Welche Unterschiede kannst du zum roten Graphen erkennen?
Kreuze jeweils die richtige Anwort an. |
|
Bewerte die Aufgaben auf deinem Laufzettel, bevor du weitermachst!
Jetzt wollen wir unsere Funktion endlich benennen. Sie gehört zu den quadratischen Funktionen. Mit diesen Funktionen werden wir uns in den nächsten Stunden beschäftigen. Dabei lernst du bestimmte Merkmale der quadratischen Funktion und ihre Handhabung.
Legen wir los!
Weiter zum nächsten Kapitel
Zurück zur Übersicht
