Weitere Aufgaben: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
K
 
(3 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 1: Zeile 1:
 +
{{Navigation SSS und SWS}}
 +
 +
 +
{| class="wikitable"
 +
|-
 +
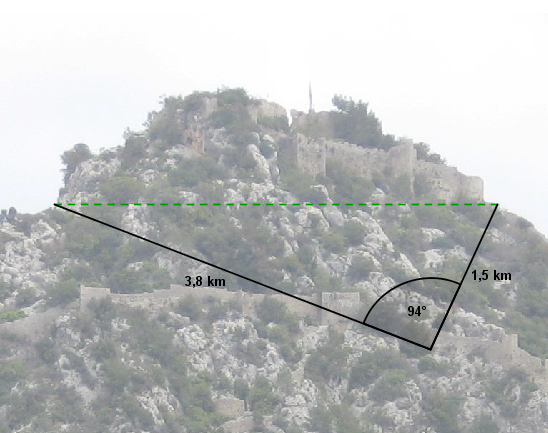
| [[Bild:Dreieck.png]] || Hier findest du noch ein paar Aufgaben zum SSS-Satz und zum SWS-Satz.<br />Versuche möglichst alle Aufgaben zu bearbeiten.
 +
|}
 +
 
<div style="border: 2px solid #0000ee; background-color:#ffffff; padding:7px;"><quiz display="simple">
 
<div style="border: 2px solid #0000ee; background-color:#ffffff; padding:7px;"><quiz display="simple">
−
{ Kann man mit den gegebenen Größen ein Dreieck ABC eindeutig konstruieren?
+
{ Zum Nachdenken:<br />
 +
Kann man mit den gegebenen Größen ein Dreieck ABC eindeutig konstruieren?
 
| typ="()" }
 
| typ="()" }
 
| Ja | Nein
 
| Ja | Nein
Zeile 23: Zeile 32:
 
</quiz>
 
</quiz>
 
<ggb_applet height="200" width="800" showResetIcon="true" filename="KS_SSS_leer.ggb" />
 
<ggb_applet height="200" width="800" showResetIcon="true" filename="KS_SSS_leer.ggb" />
 +
</div>
 +
<br />
 +
<div style="border: 2px solid #0000ee; background-color:#ffffff; padding:7px;">
 +
<quiz display="simple">
 +
Das Krümelmonster ißt einen Keks. <br />
 +
Gegeben sind die Strecken a = 3,2 cm, b = 4,3 cm und c = 3,6 cm.<br /><br />
 +
| type="{}" }
 +
Wie groß ist der Durchmesser AB des Kekses? <small>'''Runde dein Ergebnis auf <u>eine</u> Stelle nach dem Komma.'''</small><br />
 +
An der gekennzeichneten Stelle hat der Keks einen Durchmesser von { 5,0 } cm.<br />
 +
</quiz>
 +
[[Bild:KS_2.Lernpfad_Aufgaben_1.png‎]]
 
</div>
 
</div>
 
<br />
 
<br />
Zeile 36: Zeile 56:
 
[[Bild:KS_2.Lernpfad_Aufgaben_2.png‎]]
 
[[Bild:KS_2.Lernpfad_Aufgaben_2.png‎]]
 
</div>
 
</div>
 +
 +
Wenn du fertig bist, geht es hier weiter zu einem der anderen beiden Lernpfade: <br />
 +
* [[Benutzer:Kathrin_Fuchs/Wiederholungen_zum_Dreieck | Wiederholungen zum Dreieck]]<br />
 +
* [[Benutzer:Kathrin_Fuchs/WSW_und_SSW_g | WSW-Satz und SSW<sub>g</sub>-Satz]]

Aktuelle Version vom 25. Februar 2010, 11:50 Uhr

Lernpfad SSS und SWS:   SSS-Satz - SSS: Aufgaben - SSS: Lösungen - SWS-Satz - SWS: Aufgaben - SWS: Lösungen - Weitere Aufgaben


Dreieck.png Hier findest du noch ein paar Aufgaben zum SSS-Satz und zum SWS-Satz.
Versuche möglichst alle Aufgaben zu bearbeiten.

1. Zum Nachdenken:
Kann man mit den gegebenen Größen ein Dreieck ABC eindeutig konstruieren?

Ja Nein
a = 2,4 cm, b = 3,0 cm, c = 5,6 cm
a = 6,2 cm, b = 3,7 cm, c = 2,5 cm
a = 4,8 cm, b = 3,5 cm, \gamma = 74°
b = 5,9 cm, c = 7,3 cm, \alpha = 22°

Punkte: 0 / 0


1. Konstruiere mit GeoGebra ein Dreieck ABC aus den angegebenen Größen.
Öffne dazu das GeoGebra-Fenster mit Doppelklick auf das Applet!
Gib die fehlenden Größen an und runde auf eine Stelle nach dem Komma!
Achte auch auf die Größenangaben (m, dm, cm, mm)!

a) a = 5,3 cm, b = 3,1 cm, c = 4 cm, \alpha = °, \beta = °, \gamma = °
b) a = 0,45 dm, b = 55 mm, c = 6,5 cm, \alpha = °, \beta = °, \gamma = °
c) a = cm, b = 35 mm, c = 5,1 cm, \alpha = 65°, \beta = °, \gamma = °
d) a = 4,5 cm, b = mm, c = 0,05 m, \alpha = °, \beta = 52°, \gamma = °

Punkte: 0 / 0


1. Das Krümelmonster ißt einen Keks.
Gegeben sind die Strecken a = 3,2 cm, b = 4,3 cm und c = 3,6 cm.

Wie groß ist der Durchmesser AB des Kekses? Runde dein Ergebnis auf eine Stelle nach dem Komma.
An der gekennzeichneten Stelle hat der Keks einen Durchmesser von cm.

Punkte: 0 / 0

KS 2.Lernpfad Aufgaben 1.png


1. Es soll ein Tunnel in den Berg gebohrt werden, damit man schneller auf die andere Seite kommt.
Dafür haben Vermessungsingenieure ein Geländedreieck (siehe Abbildung) erstellt.

a) Ermittle die Länge des Tunnels. Runde dein Ergebnis auf eine Stelle nach dem Komma.
Der Tunnel ist km lang.
b) 100 Meter Tunnellänge kosten 1,2 Mio. Euro. Was kostet der Tunnelbau insgesammt?
Runde dein Ergebnis auf keine Stelle nach dem Komma.
Der Tunnelbau kostet insgesammt rund Mio. Euro.

Punkte: 0 / 0

KS 2.Lernpfad Aufgaben 2.png

Wenn du fertig bist, geht es hier weiter zu einem der anderen beiden Lernpfade:

Von „http://dmuw.zum.de/index.php?title=Benutzer:Kathrin_Fuchs/SSS_und_SWS/Weitere_Aufgaben&oldid=17536“