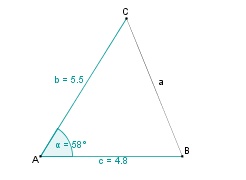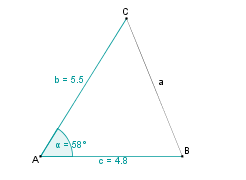SWS-Satz-3: Unterschied zwischen den Versionen
Aus DMUW-Wiki
K |
K |
||
| Zeile 62: | Zeile 62: | ||
[[Benutzer:Kathrin_Fuchs/SSS_und_SWS/Weitere Aufgaben|<math>\Rightarrow</math> Wenn du jetzt noch Zeit hast, kannst du hier weitere Aufgaben zum SSS-Satz und SWS-Satz machen.]] | [[Benutzer:Kathrin_Fuchs/SSS_und_SWS/Weitere Aufgaben|<math>\Rightarrow</math> Wenn du jetzt noch Zeit hast, kannst du hier weitere Aufgaben zum SSS-Satz und SWS-Satz machen.]] | ||
| − | Ansonsten geht es hier weiter | + | Ansonsten geht es hier weiter zu einem der anderen beiden Lernpfade: <br /> |
| + | * [[Benutzer:Kathrin_Fuchs/Wiederholungen_zum_Dreieck | Wiederholungen zum Dreieck]]<br /> | ||
| + | * [[Benutzer:Kathrin_Fuchs/WSW_und_SSW_g | WSW-Satz und SSW<sub>g</sub>-Satz]] | ||
Aktuelle Version vom 1. März 2010, 09:02 Uhr
Lernpfad SSS und SWS: SSS-Satz - SSS: Aufgaben - SSS: Lösungen - SWS-Satz - SWS: Aufgaben - SWS: Lösungen - Weitere Aufgaben
 Lass uns nun die Konstruktionen und Beschreibungen vergleichen!
Lass uns nun die Konstruktionen und Beschreibungen vergleichen!
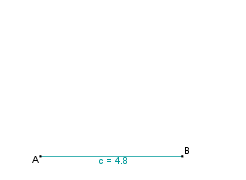
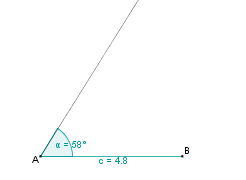
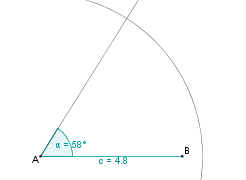
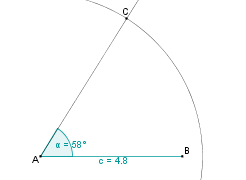
Konstruktionsbeschreibung zu a) mit c = 4,8 cm, b = 5,5 cm, 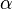 = 58°
= 58°
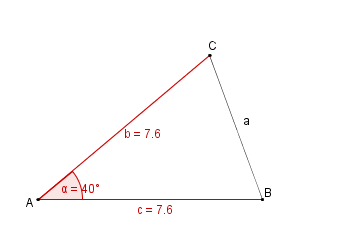
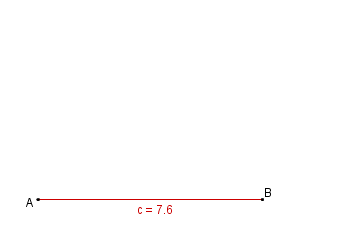
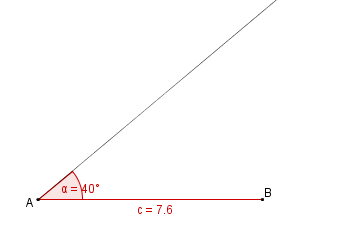
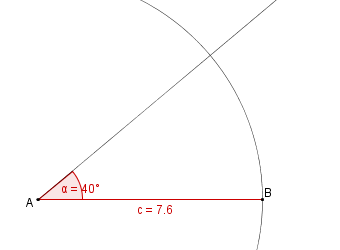
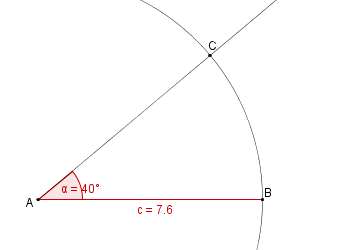
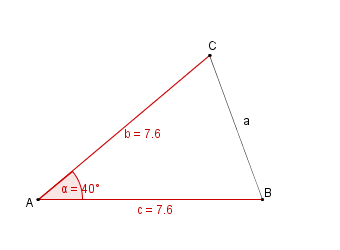
Konstruktionsbeschreibung zu b) mit c = 7,6 cm, b = c, 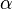 = 40°
= 40°
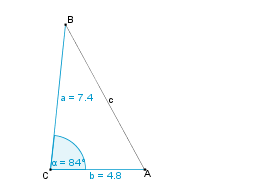
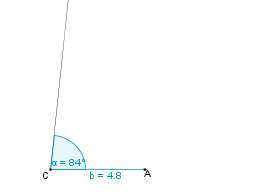
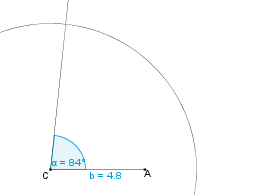
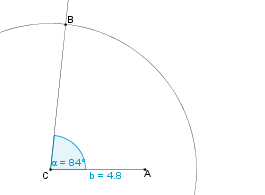
Konstruktionsbeschreibung zu c) a = 7,4 cm, b = 4,8 cm, 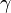 = 84°
= 84°
 Wenn du jetzt noch Zeit hast, kannst du hier weitere Aufgaben zum SSS-Satz und SWS-Satz machen.
Wenn du jetzt noch Zeit hast, kannst du hier weitere Aufgaben zum SSS-Satz und SWS-Satz machen.
Ansonsten geht es hier weiter zu einem der anderen beiden Lernpfade: