WSW-Satz-2: Unterschied zwischen den Versionen
Aus DMUW-Wiki
(Die Seite wurde neu angelegt: {| class="wikitable" |- | Bild:Dreieck.png || Wir wissen jetzt also, wie man ein Dreieck eindeutig konstruiert wenn man die Länge einer Seite und die beiden anli...) |
K |
||
| (3 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | {{Navigation WSW und SsW}} | ||
| + | |||
| + | |||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| − | | [[Bild:Dreieck.png]] || Wir wissen jetzt also, wie man ein Dreieck eindeutig konstruiert wenn man die Länge einer Seite und die beiden anliegenden Winkel kennt. | + | | [[Bild:Dreieck.png]] || Wir wissen jetzt also, wie man ein Dreieck eindeutig konstruiert, wenn man die Länge einer Seite und die beiden anliegenden Winkel kennt. |
|} | |} | ||
<br /> | <br /> | ||
| Zeile 10: | Zeile 13: | ||
<br /> | <br /> | ||
a) c <math>=</math> 7 cm, <math>\alpha</math> <math>=</math> 63°, <math>\beta</math> <math>=</math> 63° <br /> | a) c <math>=</math> 7 cm, <math>\alpha</math> <math>=</math> 63°, <math>\beta</math> <math>=</math> 63° <br /> | ||
| − | b) b <math>=</math> 4,2 cm, <math>\ | + | b) b <math>=</math> 4,2 cm, <math>\alpha</math> <math>=</math> 35°, <math>\gamma</math> <math>=</math> 115° <br /> |
c) a <math>=</math> 6,5 cm, <math>\alpha</math> <math>=</math> 65°, <math>\beta</math> <math>=</math> 75° <br /> | c) a <math>=</math> 6,5 cm, <math>\alpha</math> <math>=</math> 65°, <math>\beta</math> <math>=</math> 75° <br /> | ||
'''}} | '''}} | ||
| Zeile 18: | Zeile 21: | ||
<br /> | <br /> | ||
| − | [[Benutzer:Kathrin_Fuchs/WSW und SSW_g/WSW-Satz-3|<math>\Rightarrow</math> Wenn du die Dreiecke konstruiert und die Konstruktionsbeschreibungen notiert hast vergleiche hier dein Ergebnis.]] | + | [[Benutzer:Kathrin_Fuchs/WSW und SSW_g/WSW-Satz-3|<math>\Rightarrow</math> Wenn du die Dreiecke konstruiert und die Konstruktionsbeschreibungen notiert hast, vergleiche hier dein Ergebnis.]] |
Aktuelle Version vom 9. März 2010, 12:32 Uhr
Lernpfad WSW und SSWg: WSW-Satz - WSW: Aufgaben - WSW: Lösungen - SsW-Satz - SsW: Aufgaben - SsW: Lösungen - Weitere Aufgaben
 |
Wir wissen jetzt also, wie man ein Dreieck eindeutig konstruiert, wenn man die Länge einer Seite und die beiden anliegenden Winkel kennt. |
Lass uns ein paar Aufgaben dazu machen:
Aufgabe
Konstruiere die folgenden Dreiecke mit GeoGebra und notiere die Konstruktionsbeschreibung auf deinem Laufzettel: |
7 cm, 
Öffne dazu das GeoGebra-Fenster mit Doppelklick auf das Applet!
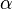
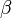
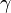
Wenn du die Dreiecke konstruiert und die Konstruktionsbeschreibungen notiert hast, vergleiche hier dein Ergebnis.
