Grundwissen: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
 
(42 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
−
Der folgende Lernpfad ist folgendermaßen gegliedert:
+
Dieser Lernpfad ist folgendermaßen gegliedert:
 
<br>I. Welche Flächen kennst Du noch?
 
<br>I. Welche Flächen kennst Du noch?
 
<br>''Hier werden Flächen mit ihrer Benennung, Form und ihren Formeln wiederholt.''
 
<br>''Hier werden Flächen mit ihrer Benennung, Form und ihren Formeln wiederholt.''
−
<br>II. Welche Besonderheiten haben die bekannten Flächen?
+
<br>II. Welche Besonderheiten der verschiedenen Flächen sind Dir noch bekannt?
 
<br>''Hier wiederholen wir wichtige Besonderheiten der verschiedenen Flächen, die immer wieder auftauchen.''
 
<br>''Hier wiederholen wir wichtige Besonderheiten der verschiedenen Flächen, die immer wieder auftauchen.''
−
<br>III. Für welche Belegung von x wird ein quadratischer Term maximal/minmal?
+
<br>III. Kennst Du noch den Unterschied zwischen "Ausklammern" und "Ausmultiplizieren"?
−
<br>''Hier wiederholen wir die Extremwertberechnung durch quadratische Ergänzung.''
+
<br>''Hier wiederholen wir wie man zwei Klammern miteinander multipliziert, bzw. einen Faktor aus den Klammern herauszieht.''
 +
<br>IV. Erinnerst Du Dich noch an die Berechnung von T<sub>min</sub>/T<sub>max</sub>?
 +
<br>''Hier wiederholen wir die Berechnung von Extremwerten mithilfe der quadratischen Ergänzung.''
 
<br>
 
<br>
  
Zeile 11: Zeile 13:
  
 
'''<span style="color: blue"><u>I. Welche Flächen kennst Du noch?</u>'''</span>  
 
'''<span style="color: blue"><u>I. Welche Flächen kennst Du noch?</u>'''</span>  
−
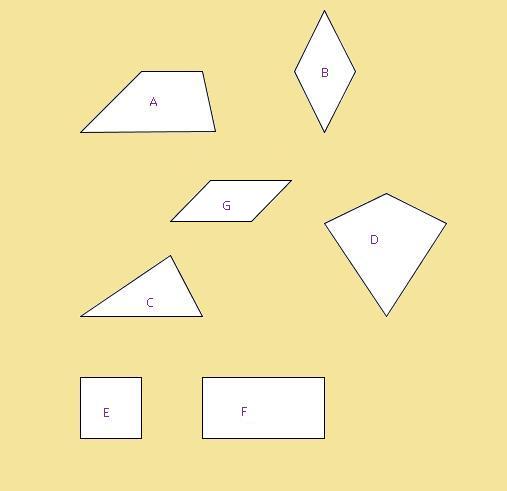
<br>'''<span style="color: blue">Ordne die folgenden Flächen ihren Benennungen und Formeln zu!</span>'''  
+
<br>'''In unserer Umwelt finden wir viele verschiedene Flächen. Weißt du noch wie diese heißen und wie man ihre Flächeninhalte bzw. Umfänge berechnet?'''
−
<br>'''<span style="color: blue">Wenn Du nicht mehr alles weißt, dann schau im Internet nach!</span>'''
+
<br>'''Ordne die folgenden Flächen ihren Benennungen und Formeln zu!'''  
 +
<br>''Du darfst das Internet als Hilfe benutzen!''
 
<br>  
 
<br>  
 
{| {{Prettytable}}
 
{| {{Prettytable}}
Zeile 19: Zeile 22:
 
|-
 
|-
 
|[[Bild: Zula3n.jpg]]|| <div class="lueckentext-quiz">  
 
|[[Bild: Zula3n.jpg]]|| <div class="lueckentext-quiz">  
−
Die Figur '''E''' heißt <u>Quadrat:</u> <br> Flächeninhalt A = '''a<sup>2</sup>'''<br> Umfang u = '''4a'''
+
Die Figur '''E''' heißt <u>Quadrat:</u> <br> Flächeninhalt A = '''a<sup>2</sup>'''<br> Umfang u = '''4∙a'''
−
<br> Die Figur '''F''' heißt <u>Rechteck:</u> <br> Flächeninhalt A = '''a*b'''<br> Umfang u = '''2a+2b'''
+
<br> Die Figur '''F''' heißt <u>Rechteck:</u> <br> Flächeninhalt A = '''a∙b'''<br> Umfang u = '''2∙a+2∙b'''
−
<br> Die Figur '''C''' heißt <u>Dreieck:</u> <br> Flächeninhalt A = '''1/2*g*h'''<br> Umfang u = '''a+b+c'''
+
<br> Die Figur '''C''' heißt <u>Dreieck:</u> <br> Flächeninhalt A = '''½∙g∙h'''<br> Umfang u = '''a+b+c'''
−
<br> Die Figur '''B''' heißt <u>Raute:</u> <br> Flächeninhalt A = '''1/2*e*f'''<br> Umfang u = '''4a'''
+
<br> Die Figur '''B''' heißt <u>Raute:</u> <br> Flächeninhalt A = '''½∙e∙f'''<br> Umfang u = '''4∙a'''
−
<br> Die Figur '''A''' heißt <u>Trapez:</u> <br> Flächeninhalt A = '''m*h'''<br> Umfang u = '''a+b+c+d'''
+
<br> Die Figur '''A''' heißt <u>Trapez:</u> <br> Flächeninhalt A = '''m∙h'''<br> Umfang u = '''a+b+c+d'''
−
<br> Die Figur '''D''' heißt <u>Drachen:</u> <br> Flächeninhalt A = '''1/2*e*f'''<br> Umfang u = '''2a+2b'''
+
<br> Die Figur '''D''' heißt <u>Drachen:</u> <br> Flächeninhalt A = '''½∙e∙f'''<br> Umfang u = '''2∙a+2∙b'''
−
<br> Die Figur '''G''' heißt <u>Parallelogramm:</u> <br> Flächeninhalt A = '''1/2*g*h'''<br> Umfang u = '''2a+2b'''
+
<br> Die Figur '''G''' heißt <u>Parallelogramm:</u> <br> Flächeninhalt A = '''½∙g∙h'''<br> Umfang u = '''2∙a+2∙b'''
 
</div>  
 
</div>  
 
|}
 
|}
−
<br>
 
−
'''Hast Du alle Lücken richtig gefüllt?'''
 
−
<br>'''Dann kannst Du dir jetzt das folgende Dokument herunterladen und ausdrucken!'''
 
−
<br>
 
 
<br>
 
<br>
 
<br>
 
<br>
Zeile 38: Zeile 37:
  
 
<span style="color: blue">'''<u>II. Welche Besonderheiten der verschiedenen Flächen sind Dir noch bekannt?</u>'''</span>
 
<span style="color: blue">'''<u>II. Welche Besonderheiten der verschiedenen Flächen sind Dir noch bekannt?</u>'''</span>
−
<br>'''<span style="color: blue">Kreuze die richtigen Gesetzmäßigkeiten an!</span>'''  
+
<br>'''Jede Fläche hat Besonderheiten. Kennst du welche?'''
 +
<br>'''Kreuze die richtigen Gesetzmäßigkeiten an!'''  
 
<br> <u>Quadrat:</u>  
 
<br> <u>Quadrat:</u>  
 
<div class="multiplechoice-quiz">
 
<div class="multiplechoice-quiz">
Zeile 78: Zeile 78:
 
<br> <u>Trapez:</u>
 
<br> <u>Trapez:</u>
 
<div class="multiplechoice-quiz">
 
<div class="multiplechoice-quiz">
 +
(!Die gegenüberliegenden Seiten sind gleich lang.)
 +
(Zwei gegenüberliegende Seiten sind parallel.)
 +
(Die benachbarten Winkel ergänzen sich zu 180°.)
 +
(!Die gegenüberliegenden Winkel sind gleich groß.)
 +
</div>
 +
<br>
 +
<br> <u>Drachen:</u>
 +
<div class="multiplechoice-quiz">
 +
(!Der Drachen ist eine besondere Raute.)
 +
(Die Diagonalen stehen senkrecht aufeinander.)
 +
(Nur eine Diagonale wird halbiert.)
 +
(!Die gegenüberliegenden Winkel sind gleich groß.)
 +
(Je zwei Seiten sind gleich lang.)
 +
</div>
 +
<br>
 
<br> <u>Parallelogramm:</u>  
 
<br> <u>Parallelogramm:</u>  
 
<div class="multiplechoice-quiz">
 
<div class="multiplechoice-quiz">
Zeile 89: Zeile 104:
 
</div>
 
</div>
 
<br>
 
<br>
 +
<br>'''Hast Du nicht alle Besonderheiten gefunden? Berate Dich mit Deinem Partner!'''
 +
 +
----
 +
 +
<span style="color: blue">'''<u>III. Kennst Du noch den Unterschied zwischen "Ausmultiplizieren" und "Ausklammern"?</u>'''</span>
 +
<br>'''"Ausmultiplizieren" und "Ausklammern" klingt ähnlich. Doch was ist der Unterschied?'''
 +
<br><span style="color: blue">'''a) Ausmultiplizieren'''</span>
 +
<br>'''Beim Ausmultiplizieren "nimmt man zwei (oder mehr) Klammern miteinander Mal".
 +
<br>'''Dabei sollte man wie folgt vorgehen:'''
 +
<br>[[Bild: Ausmultiplizieren.jpg]]
 +
<br>'''Die Theorie ist jetzt klar, also ab zur Praxis:'''
 +
<br>[[media:Arbeitsblatt 1.doc|Arbeitsblatt 1]]
 +
<br>'''Wenn Du alle Aufgaben gelöst hast, dann tausche mit deinem Partner und korrigiere seine Aufgaben!'''
 
<br>
 
<br>
 +
<br>
 +
<br><span style="color: blue">'''b) Ausklammern'''</span>
 +
<br>'''Beim Ausklammern möchte man einen Faktor aus der Klammer herausziehen. Das macht man folgendermaßen:'''
 +
<br>[[Bild: Ausklammern.jpg]]
 +
<br>'''Das versuchen wir am besten gleich selbst auf dem nächsten Arbeitsblatt:'''
 +
<br>[[media:Arbeitsblatt 2.doc|Arbeitsblatt 2]]
 +
<br>'''Hast Du alle Aufgaben gelöst? Dann tausche wieder mit deinem Partner und korrigiere seine Aufgaben!'''
 +
 +
----
 +
 +
<span style="color: blue">'''<u>III. IV. Erinnerst Du Dich noch an die Berechnung von T<sub>min</sub>/T<sub>max</sub>?</u>'''</span>
 +
<br>'''Für die Berechnung von T<sub>min</sub>/T<sub>max</sub> braucht man die Binomischen Formeln. Doch was war das nochmal?'''
 +
<br><span style="color: blue">'''a) Binomische Formeln'''</span>
 +
<br>'''Weißt Du noch wieviele binomische Formeln es überhaupt gibt?'''
 +
<br><div class="multiplechoice-quiz">
 +
(!2) (!4) (3)
 +
</div>
 +
<br>'''Und welche sind das?'''
 +
<br><div class="lueckentext-quiz">
 +
<br> (a - b)<sup>2</sup> = a<sup>2</sup> + 2ab - b<sup>2</sup> '''Falsch'''
 +
<br> (a + b)(a - b) = a<sup>2</sup> - b<sup>2</sup> '''Richtig'''
 +
<br> (a + b)<sup>2</sup> = a<sup>2</sup> + 2ab + b<sup>2</sup> '''Richtig'''
 +
<br> (a - b)<sup>2</sup> = a<sup>2</sup> - 2ab + b<sup>2</sup> '''Richtig'''
 +
<br> (a + b)(a - b) = b<sup>2</sup> - a<sup>2</sup> '''Falsch'''
 +
</div>
 +
<br>
 +
<br>'''Nun kennen wir die Anzahl der Binomischen Formeln und wie diese lauten, doch kannst Du diese auch anwenden? Um dies zu üben hab ich ein Arbeitsblatt für Dich vorbereitet. <br> Wenn Du alle Aufgaben gelöst hast, dann lass sie wieder von deinem Partner kontrollieren!'''
 +
<br>[[media:Arbeitsblatt 3n.doc|Arbeitsblatt 3]]
 +
<br>
 +
<br>'''Für die quadratische Ergänzung sind die Binomischen Formeln sehr wichtig.<br>Schauen wir uns an warum!'''
 +
<br><span style="color: blue">'''b) Quadratische Ergänzung'''</span>
 +
<br>'''In der Präsentation wird eine Beispielaufgabe für eine quadratische Ergänzung vorgerechnet. Schau sie Dir gemeinsam mit Deinem Partner genau an und versucht die einzelnen Schritte schriftlich auf dem nächsten Arbeitsblatt festzuhalten.'''
 +
<br>
 +
<br>[[media:quadratische Ergänzung n.pps|Präsentation]]
 +
<br>[[media:Arbeitsblatt 4.doc|Arbeitsblatt 4]]
 +
<br>
 +
<br>'''Mithilfe eures "Rezeptes" könnt Ihr das folgende Arbeitsblatt - jeder für sich - lösen.'''
 +
<br>
 +
<br>[[media:Arbeitsblatt 5.doc|Arbeitsblatt 5]]
 +
----
 +
 +
<br>'''Spitze! Du hast den ersten Lernpfad erfolgreich gemeistert!'''
 +
<br>'''Jetzt wollen wir herausfinden was "Funktionale Abhängigkeit" bedeutet und wofür man diese brauchen kann!'''

Aktuelle Version vom 8. Juli 2010, 10:04 Uhr

Dieser Lernpfad ist folgendermaßen gegliedert:
I. Welche Flächen kennst Du noch?
Hier werden Flächen mit ihrer Benennung, Form und ihren Formeln wiederholt.
II. Welche Besonderheiten der verschiedenen Flächen sind Dir noch bekannt?
Hier wiederholen wir wichtige Besonderheiten der verschiedenen Flächen, die immer wieder auftauchen.
III. Kennst Du noch den Unterschied zwischen "Ausklammern" und "Ausmultiplizieren"?
Hier wiederholen wir wie man zwei Klammern miteinander multipliziert, bzw. einen Faktor aus den Klammern herauszieht.
IV. Erinnerst Du Dich noch an die Berechnung von Tmin/Tmax?
Hier wiederholen wir die Berechnung von Extremwerten mithilfe der quadratischen Ergänzung.

I. Welche Flächen kennst Du noch?
In unserer Umwelt finden wir viele verschiedene Flächen. Weißt du noch wie diese heißen und wie man ihre Flächeninhalte bzw. Umfänge berechnet?
Ordne die folgenden Flächen ihren Benennungen und Formeln zu!
Du darfst das Internet als Hilfe benutzen!

Verschiedene Flächen: Benennung und Formeln:
Zula3n.jpg

Die Figur E heißt Quadrat:
Flächeninhalt A = a2
Umfang u = 4∙a
Die Figur F heißt Rechteck:
Flächeninhalt A = a∙b
Umfang u = 2∙a+2∙b
Die Figur C heißt Dreieck:
Flächeninhalt A = ½∙g∙h
Umfang u = a+b+c
Die Figur B heißt Raute:
Flächeninhalt A = ½∙e∙f
Umfang u = 4∙a
Die Figur A heißt Trapez:
Flächeninhalt A = m∙h
Umfang u = a+b+c+d
Die Figur D heißt Drachen:
Flächeninhalt A = ½∙e∙f
Umfang u = 2∙a+2∙b
Die Figur G heißt Parallelogramm:
Flächeninhalt A = ½∙g∙h
Umfang u = 2∙a+2∙b



II. Welche Besonderheiten der verschiedenen Flächen sind Dir noch bekannt?
Jede Fläche hat Besonderheiten. Kennst du welche?
Kreuze die richtigen Gesetzmäßigkeiten an!
Quadrat:

(Alle Winkel sind gleich groß.) (Die Diagonalen halbieren sich und sind gleich lang.) (!Die vier Seiten sind nicht gleich lang.) (Die Diagonalen stehen senkrecht aufeinander.) (!Das Quadrat ist keine besondere Raute.)



Rechteck:

(Alle Winkel sind gleich groß.) (!Alle Seiten sind gleich lang.) (!Die gegenüberliegenden Seiten sind nicht immer parallel.) (Die Diagonalen halbieren sich und sind gleich lang) (!Die Diagonalen stehen stets senkrecht aufeinander.)



Dreieck:

(In einem gleichseitigen Dreieck sind alle Winkel gleich groß.) (!Das gleichschenklige Dreieck hat drei gleich lange Seiten.) (Die Basiswinkel eines gleischenkligen Dreiecks sind gleich groß.) (!Den Flächeninhalt kann man nicht statt A = 1/2*g*h mit A = 1/2*a*b berechnen.) (Das gleichseitige Dreieck ist ein besonderes gleischschenkliges Dreieck.) (!Das gleichschenklige Dreieck ist nicht symmetrisch zu seiner Höhe.)



Raute:

(!Die Raute ist ein besonderes Quadrat.) (Alle Seiten der Raute sind gleich lang.) (Die Raute ist ein besonderer Drachen.) (!Die Winkel der Raute sind gleich groß.) (Die Diagonalen halbieren sich gegenseitig und stehen senkrecht aufeinander.)



Trapez:

(!Die gegenüberliegenden Seiten sind gleich lang.) (Zwei gegenüberliegende Seiten sind parallel.) (Die benachbarten Winkel ergänzen sich zu 180°.) (!Die gegenüberliegenden Winkel sind gleich groß.)



Drachen:

(!Der Drachen ist eine besondere Raute.) (Die Diagonalen stehen senkrecht aufeinander.) (Nur eine Diagonale wird halbiert.) (!Die gegenüberliegenden Winkel sind gleich groß.) (Je zwei Seiten sind gleich lang.)



Parallelogramm:

(!Alle Seiten sind gleich lang.) (Die gegenüberliegenden Seiten sind gleich lang.) (Die gegenüberliegenden Seiten sind stets parallel.) (!Alle Winkel sind gleich groß.) (Die benachbarten Winkel ergänzen sich zu 180°.) (!Die Diagonalen halbieren sich nicht.) (Gegenüberliegende Winkel sind immer gleich groß.)



Hast Du nicht alle Besonderheiten gefunden? Berate Dich mit Deinem Partner!

III. Kennst Du noch den Unterschied zwischen "Ausmultiplizieren" und "Ausklammern"?
"Ausmultiplizieren" und "Ausklammern" klingt ähnlich. Doch was ist der Unterschied?
a) Ausmultiplizieren
Beim Ausmultiplizieren "nimmt man zwei (oder mehr) Klammern miteinander Mal".
Dabei sollte man wie folgt vorgehen:
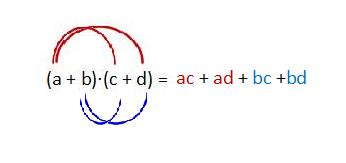
Ausmultiplizieren.jpg
Die Theorie ist jetzt klar, also ab zur Praxis:
Arbeitsblatt 1
Wenn Du alle Aufgaben gelöst hast, dann tausche mit deinem Partner und korrigiere seine Aufgaben!


b) Ausklammern
Beim Ausklammern möchte man einen Faktor aus der Klammer herausziehen. Das macht man folgendermaßen:
Ausklammern.jpg
Das versuchen wir am besten gleich selbst auf dem nächsten Arbeitsblatt:
Arbeitsblatt 2
Hast Du alle Aufgaben gelöst? Dann tausche wieder mit deinem Partner und korrigiere seine Aufgaben!

III. IV. Erinnerst Du Dich noch an die Berechnung von Tmin/Tmax?
Für die Berechnung von Tmin/Tmax braucht man die Binomischen Formeln. Doch was war das nochmal?
a) Binomische Formeln
Weißt Du noch wieviele binomische Formeln es überhaupt gibt?


(!2) (!4) (3)


Und welche sind das?



(a - b)2 = a2 + 2ab - b2 Falsch
(a + b)(a - b) = a2 - b2 Richtig
(a + b)2 = a2 + 2ab + b2 Richtig
(a - b)2 = a2 - 2ab + b2 Richtig
(a + b)(a - b) = b2 - a2 Falsch



Nun kennen wir die Anzahl der Binomischen Formeln und wie diese lauten, doch kannst Du diese auch anwenden? Um dies zu üben hab ich ein Arbeitsblatt für Dich vorbereitet.
Wenn Du alle Aufgaben gelöst hast, dann lass sie wieder von deinem Partner kontrollieren!
Arbeitsblatt 3

Für die quadratische Ergänzung sind die Binomischen Formeln sehr wichtig.
Schauen wir uns an warum!
b) Quadratische Ergänzung
In der Präsentation wird eine Beispielaufgabe für eine quadratische Ergänzung vorgerechnet. Schau sie Dir gemeinsam mit Deinem Partner genau an und versucht die einzelnen Schritte schriftlich auf dem nächsten Arbeitsblatt festzuhalten.

Präsentation
Arbeitsblatt 4

Mithilfe eures "Rezeptes" könnt Ihr das folgende Arbeitsblatt - jeder für sich - lösen.

Arbeitsblatt 5


Spitze! Du hast den ersten Lernpfad erfolgreich gemeistert!
Jetzt wollen wir herausfinden was "Funktionale Abhängigkeit" bedeutet und wofür man diese brauchen kann!

Von „http://dmuw.zum.de/index.php?title=Lernpfade/Relation_und_Funktion/Grundwissen&oldid=23569“