Würfelvolumen: Unterschied zwischen den Versionen
(→Volumen von Würfel und Quader) |
(→Volumen von Würfel und Quader) |
||
| (4 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | __NOTOC__ | ||
<div style="border: 2px solid lightgreen; background-color:#ffffff; padding:7px;"> <br> | <div style="border: 2px solid lightgreen; background-color:#ffffff; padding:7px;"> <br> | ||
| − | =='''<u>Volumen | + | =='''<u>Das Volumen eines Würfels</u>'''== |
<br> | <br> | ||
<br> | <br> | ||
| Zeile 7: | Zeile 8: | ||
| width="650" | | | width="650" | | ||
<div style="padding:10px;background:#ffffff;border:1px ;"> | <div style="padding:10px;background:#ffffff;border:1px ;"> | ||
| − | ==='''<u>Einheitswürfel</u>'''=== | + | ==='''<u>Der Einheitswürfel</u>'''=== |
<br> | <br> | ||
<br> | <br> | ||
| Zeile 81: | Zeile 82: | ||
</div> | </div> | ||
|} | |} | ||
| − | + | <br> | |
| + | <br> | ||
| + | <br> | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | width="1050" | | ||
| + | <div style="padding:10px;background:#ffffff;border:1px ;"> | ||
| + | ==='''<u>Präsentation</u>'''=== | ||
| + | <br> | ||
| + | Hast du alles verstanden? Super! Vielleicht darfst du gleich deinen Klassenkameraden erklären, wie man das Volumen von einem Würfel berechnet. Versuche es doch einmal bei deinem Banknachbarn! Wie würdest du es ihm erklären? | ||
</div> | </div> | ||
| + | |} | ||
| + | </div> | ||
| + | <br> | ||
| + | <br> | ||
| + | [[../Knobelaufgabe2|'''Hier geht es zu den Knobelaufgaben für die Schnellen''']] | ||
<br> | <br> | ||
<br> | <br> | ||
| − | + | [[../|'''Hier geht es zurück zur Gruppenübersicht''']] | |
Aktuelle Version vom 21. Juli 2010, 13:55 Uhr
Das Volumen eines Würfels
Der Einheitswürfel
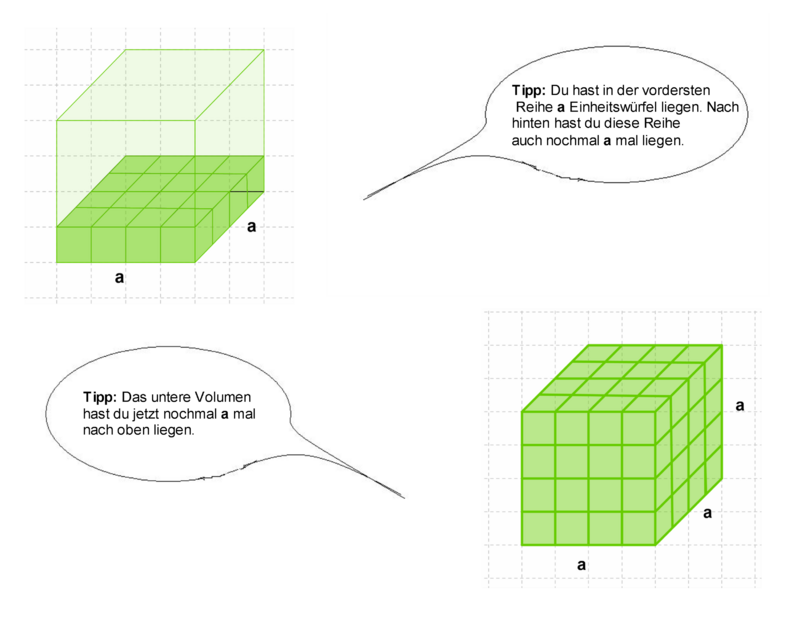
Es passen 27(Einheitswürfel) in den großen Würfel rein. |
|
Das Würfelvolumen
|
Präsentation
|
Hier geht es zu den Knobelaufgaben für die Schnellen
Hier geht es zurück zur Gruppenübersicht