Würfel- und Quaderoberfläche: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
(→‎Das Quadernetz)
 
(9 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 1: Zeile 1:
 +
__NOTOC__
 
<div style="border: 2px solid lightgreen; background-color:#ffffff; padding:7px;"> <br>
 
<div style="border: 2px solid lightgreen; background-color:#ffffff; padding:7px;"> <br>
 
=='''<u>Oberfläche von einem  Quader und einem Würfel</u>'''==
 
=='''<u>Oberfläche von einem  Quader und einem Würfel</u>'''==
Zeile 11: Zeile 12:
 
Schaue dir das Applet doch mal genauer an. <br>
 
Schaue dir das Applet doch mal genauer an. <br>
 
<br>
 
<br>
−
::<ggb_applet height="500" width="900" filename="SchiebereglerNetz2.ggb"/>
+
::<ggb_applet height="500" width="900" filename="SchiebereglerNetz5.ggb"/>
 
<br>
 
<br>
−
Du hast hier gesehen, dass ein Netz ensteht, wenn du den Quader auseinanderklappst. So ein Netz kann dir bei der Berrechnung der Oberfläche helfen. Schaue dir dazu doch die nächste Aufgabe an.
+
<br>
 +
Du hast hier gesehen, dass ein Netz ensteht, wenn du den Quader auseinanderklappst. So ein Netz kann dir bei der Berrechnung der Oberfläche helfen. Schaue dir dazu doch die nächste Aufgabe an. Beachte: Ein Würfel ist ein Spezialfall vom Quader, bei dem alle Kantenlängen gleich groß sind!
 
</div>
 
</div>
 
|}
 
|}
Zeile 22: Zeile 24:
 
| width="550" |
 
| width="550" |
 
<div style="padding:10px;background:#ffffff;border:1px ;">
 
<div style="padding:10px;background:#ffffff;border:1px ;">
 +
 
==='''<u>Die Würfeloberfläche (O<sub>W</sub>)</u>'''===
 
==='''<u>Die Würfeloberfläche (O<sub>W</sub>)</u>'''===
 
<br>
 
<br>
Zeile 34: Zeile 37:
 
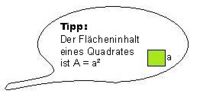
Wie groß ist diese '''Oberfläche''', wenn die Kantenlänge a beträgt?(!O<sub>W</sub> = 6·a) (O<sub>W</sub> = 6·a²) (!O<sub>W</sub> = 6·a+a) (!O<sub>W</sub> = a·a)
 
Wie groß ist diese '''Oberfläche''', wenn die Kantenlänge a beträgt?(!O<sub>W</sub> = 6·a) (O<sub>W</sub> = 6·a²) (!O<sub>W</sub> = 6·a+a) (!O<sub>W</sub> = a·a)
 
</div>  
 
</div>  
−
  || [[Bild:VerpackungWürfel.jpg|500px]]
+
  || [[Bild:VerpackungWürfel2.jpg|500px]]
 
</div>
 
</div>
 
|}
 
|}
Zeile 85: Zeile 88:
 
| width="1050" |
 
| width="1050" |
 
<div style="padding:10px;background:#ffffff;border:1px ;">
 
<div style="padding:10px;background:#ffffff;border:1px ;">
−
==='''<u>Das Auqarium</u>'''===
+
==='''<u>Die Truhe</u>'''===
 
<br>
 
<br>
−
::::::::[[Bild:Aquarium5.jpg|300px]]&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;[[Bild:Sonne5.jpg|200px]]
+
Hast du verstanden wie man die Oberfläche berechnet? Dann versuche dich doch mal an dieser Aufgabe.
−
<small>Beachte: Berechne die Aufgaben auf ein Platt Papier. Tipp: Der Flächeninhalt für ein Rechteck mit den Kanten a und b ist a·b.</small>
+
 
<div class="lueckentext-quiz">
 
<div class="lueckentext-quiz">
−
Joans muss sein '''[[Bild:Aquarium5.jpg|60px]]''' mit einer Wäremeschutzfolie bekleben, damit es den [[Bild:Fische5.jpg|60px]] bei diesem heißen Sommer nicht zu warm wird. Es reicht, wenn er die Decke und die '''Seitenwände'''beklebt. Jonas braucht ür die linke und rechte Seite zwei Folien die zusammen '''1000 (cm²)''' groß sind, zwei die je '''1250 cm²''' groß sind und eine die '''1000(cm²)''' groß ist. Insgesamt braucht Jonas Folie für '''4500(cm²)'''.
+
Hanna möchte ihre Truhe mit einem grünen Stoff beziehen. Damit sie die ganze Truhe beziehen kann, braucht sie '''1000(cm²)''' Stoff.
 +
|[[Bild:Truhe.jpg|200px]]
 
</div>
 
</div>
 
&nbsp;
 
&nbsp;
 
</div>
 
</div>
 
|}
 
|}
 +
<br>
 +
<br>
 +
<br>
 +
{| class="wikitable"
 +
|-
 +
| width="1050" |
 +
<div style="padding:10px;background:#ffffff;border:1px ;">
 +
==='''<u>Präsentation</u>'''===
 +
<br>
 +
Hast du alles verstanden? Super! Vielleicht darfst du gleich deinen Klassenkameraden erklären, wie man die Oberfläche von einem Quader und von einem Würfel berechnet. Versuche es doch einmal bei deinem Banknachbarn! Wie würdest du es ihm erklären?
 
</div>
 
</div>
 +
|}
 +
</div>
 +
<br>
 +
<br>
 +
[[../Knobelaufgabe1|'''Hier geht es zu den Knobelaufgaben für die Schnellen''']]
 
<br>
 
<br>
 
<br>
 
<br>
−
[[Bild:PfeilLinks.png|50px]] [[../|'''Hier geht es zurück zur Gruppenübersicht''']]
+
[[../|'''Hier geht es zurück zur Gruppenübersicht''']]

Aktuelle Version vom 21. Juli 2010, 15:17 Uhr


Oberfläche von einem Quader und einem Würfel



Das Quadernetz


Schaue dir das Applet doch mal genauer an.



Du hast hier gesehen, dass ein Netz ensteht, wenn du den Quader auseinanderklappst. So ein Netz kann dir bei der Berrechnung der Oberfläche helfen. Schaue dir dazu doch die nächste Aufgabe an. Beachte: Ein Würfel ist ein Spezialfall vom Quader, bei dem alle Kantenlängen gleich groß sind!



Die Würfeloberfläche (OW)


Jonas hat in Mathe Hausaufgaben aufbekommen.
Er soll eine quadratische Verpackung
aufschneiden und die Oberfläche bestimmen.

Tipp1.jpg

Überlege dir zusammen mit deiner Gruppe wie groß die Fläche ist. Rechnet sie auf einem Blatt Papier aus. Die Maße könnt ihr dem Bild entnehmen.(!40 cm²)(54 cm²)(!18 cm²)(!36 cm²)

Wie groß ist diese Oberfläche, wenn die Kantenlänge a beträgt?(!OW = 6·a) (OW = 6·a²) (!OW = 6·a+a) (!OW = a·a)

VerpackungWürfel2.jpg




Das Baumhaus

Beachte: In die grünen Felder ziehst du die passende Lösung von unten rein. In die weißen Felder trägst du deine Lösung selbst ein. Rechne im Kopf.

Hanna hat von ihrem Papa ein Baumhaus1.jpg gebaut bekommen. Bevor er es in dem Baum fest verankert, möchte sie es noch gerne verschönern. Türen und Fenster hat der Papa noch nicht ausgepart. Sie hat sich dazu entschlossen es von außen ganz in FarbeGelb.jpg anzumalen. Sie braucht für 54(m²) Farbe. Eine Flasche Farbe reicht für 10 m², somit müssen ihre Eltern 6(Flaschen) Farbe kaufen.

Baumhaus1.jpg




Quaderoberfläche (OQ)


Bsp.:Ich habe ein Würfelnetz Wü1.png. Ich lege mir die Flächen so Wü2.png, dass die Flächen a² sechs mal nebeneinander liegen. OW ist dann 6·a²
Rechts im Applet kannst auch du die Flächen verschieben. Gehe wie im Beispiel vor und kontrolliere, welche Formeln stimmen.
Es können mehrere Lösungen stimmen.

Ist die Formel OQ = 6·a² richtig? (!ja) (nein)

Ist die Formel OQ = 2·a·b+2·b·c+2·a·c richtig? (ja) (!nein)

Ist die Formel OQ = 2·(a·b+b·c+a·c) richtig? (ja) (!nein)

Ist die Formel OQ = 6·a·b·c richtig? (!ja) (nein)




Die Truhe


Hast du verstanden wie man die Oberfläche berechnet? Dann versuche dich doch mal an dieser Aufgabe.

Hanna möchte ihre Truhe mit einem grünen Stoff beziehen. Damit sie die ganze Truhe beziehen kann, braucht sie 1000(cm²) Stoff.

Truhe.jpg

 




Präsentation


Hast du alles verstanden? Super! Vielleicht darfst du gleich deinen Klassenkameraden erklären, wie man die Oberfläche von einem Quader und von einem Würfel berechnet. Versuche es doch einmal bei deinem Banknachbarn! Wie würdest du es ihm erklären?



Hier geht es zu den Knobelaufgaben für die Schnellen

Hier geht es zurück zur Gruppenübersicht

Von „http://dmuw.zum.de/index.php?title=Lernpfade/Quader_und_Würfel_2/Würfel-_und_Quaderoberfläche&oldid=24718“