Grundlagen der Zerlegungsgleichheit von Figuren: Unterschied zwischen den Versionen
(→1.2 Los geht´s: Teste Dein Wissen!) |
(Tabelle repariert) |
||
| Zeile 208: | Zeile 208: | ||
<div style="border: 2px solid red; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid red; background-color:#ffffff; padding:7px;"> | ||
{| | {| | ||
| − | [[Bild:Ebert_MotivatorMerke.jpg]]||Zwei Figuren sind <span style="color: red">ergänzungsgleich</span>, wenn man sie durch <span style="color: red">Ergänzung mit kongruenten Teilfiguren</span> in <span style="color: red">zerlegungsgleiche Figuren</span> umwandeln kann. <span style="color: red">Ergänzungsgleiche</span> Figuren sind daher auch <span style="color: red">zerlegungsgleich</span>.Ergänzungsgleiche Figuren besitzen den gleichen Flächeninhalt. | + | | [[Bild:Ebert_MotivatorMerke.jpg]] |
| + | || Zwei Figuren sind <span style="color: red">ergänzungsgleich</span>, wenn man sie durch <span style="color: red">Ergänzung mit kongruenten Teilfiguren</span> in <span style="color: red">zerlegungsgleiche Figuren</span> umwandeln kann. <span style="color: red">Ergänzungsgleiche</span> Figuren sind daher auch <span style="color: red">zerlegungsgleich</span>.Ergänzungsgleiche Figuren besitzen den gleichen Flächeninhalt. | ||
|} | |} | ||
</div> | </div> | ||
| − | |||
===Vertiefen und Übung === | ===Vertiefen und Übung === | ||
Version vom 9. Juli 2009, 12:23 Uhr
Auf dieser Seite lernst Du die Eigenschaften der Zerlegungsgleichheit von Figuren kennen.
Bearbeite die Aufgaben sorgfältig!
Nicht mogeln...schaue erst die Lösungen an, wenn du die Aufgaben selbstsändig bearbeitet hast!
Denn nur so lernst du am Besten!
1. Grundlagen der Zerlegungsgleichheit von Figuren
1.1 Wiederholung des Kongruenzbegriffes
- Weißt Du noch was man unter Kongruenz von Figuren versteht??
- Eine Wiederholung kann nicht schaden.
1.2 Los geht´s: Teste Dein Wissen!
- Ein anderes Wort für Kongruenz ist (dnelkiugchehcgitse)
- Hinweis: Kongruente Figuren kann man zur Deckung bringen
Aufgabe: Kongruente Dreiecke
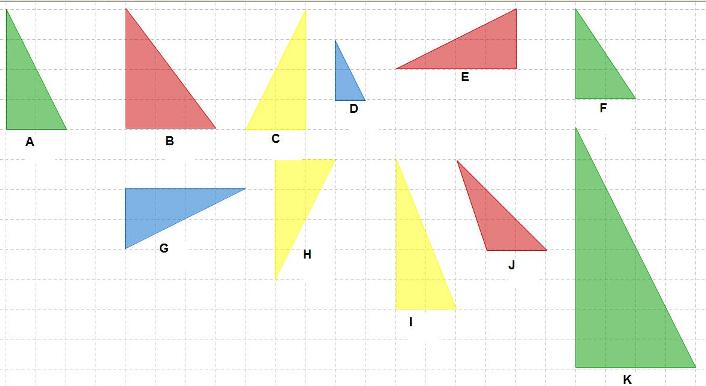
- Findest Du alle Dreiecke, die zum Dreieck A kongruent sind?
Gib die Buchstaben an und begründe anschließend warum.
- War Deine Lösung richtig?
Kleines Quiz
Achtung!! Mehrere Antworten sind möglich!
1.3 Das sollest du also wissen
 |
Zwei Figuren sind zueinander kongruent, wenn sie durch (ngesrhbciuev), (dguenhr) oder (egepiuslgn) ineinander überführt werden können. Diese drei Abbildungen nennt man daher auch (zukgonnre)-abbildungen. |
1.4 Wofür können wir die Kongruenz von Figuren gebrauchen?
- Du kennst sicher ein paar Anwendungsbeispiele wofür man die Eigenschaften der man die Kongruenz von Figuren nutzen kann.
Dazu gehört zum Beispiel die Konstruktion von Dreiecken, wofür man die Kongruenzsätze benötigt. Kennst Du noch alle davon? Ordne die richtige Abkürzung der Beschreibung zu!
Zwei Dreiecke, die in ihren drei Seitenlängen übereinstimmen, sind kongruent:
Zwei Dreiecke, die in einer Seitenlänge und in den dieser Seite anliegenden Winkeln übereinstimmen, sind kongruent:
Zwei Dreiecke, die in zwei Seitenlängen und in dem eingeschlossenen Winkel übereinstimmen, sind kongruent:
Zwei Dreiecke, die in zwei Seitenlängen und in jenem Winkel übereinstimmen, der der längeren Seite gegenüberliegt, sind kongruent:
SSS-SatzSsW-SatzSWS-SatzWSW-Satz
- Im nächsten Abschnitt lernst Du ein weiteres Anwendungsbeispiel kennen
2. Zerlegungsgleichheit von Figuren
2.1 Eine Einführung
Kapitän Check Aufgabe: Welche ist die größte Insel?
- Aufgabenstellung:
: Du siehst hier die 3 schwarzen Inseln. Darunter befinden sich alle Teilfiguren, mit denen man die Inseln vollständig zusammensetzen kann. Klicke :die jeweiligen Kästchen an, um die Teilfiguren auf die Inseln zu legen.
- Lege die Teilfiguren per Mausklick von Links nach Rechts auf die Insel
- Überlege Dir zunächst selbst, wo die nächste Teilfigur platziert werden könnte.
- Was fällt Dir auf? Welche ist die größte Insel?
- Was fällt Dir auf? Welche ist die größte Insel?? Begründe Deine Antwort!
Die größte Insel ist (entweder Isola Grande, Isola Bella oder Isola Piccola eintragen)
|
Figur A und C nennt man daher auch zerlegungsgleich, |
2.3 Das Prinzip der Zerlegungsgleichheit
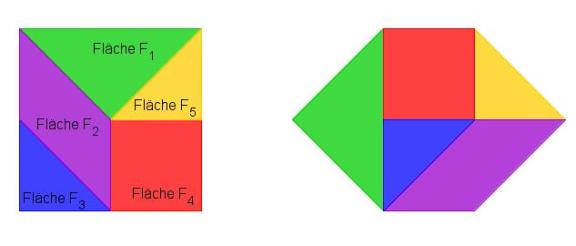
- Das Sechseck und das Quadrat wurden in jeweils fünf Teilfiguren zerlegt.
- Diese Teilfiguren sind paarweise zueinander kongruent, d.h. es gibt immer ein Paar zueinander kongruenter Figuren.
- Aus den Eigenschaften der Kongruenz ergibt sich daher, dass diese Teilfiguren den gleichen Flächeninhalt besitzen.
- Der Flächeninhalt des Quadrates setzt sich in diesem Beispiel aus den Flächeninhalten der Teilfiguren F1 bis F5 zusammen.
Ergänze die fehlenden Felder
FQuadrat = + + + +
ebenso gilt aber auch:
F1 + F2 + F3 + F4 + F5 =
- Somit haben Sechseck und Quadrat in dem Beispiel den !
F3F5F1F4FSechseckF2gleichen Flächeninhalt
<br
 Der Flächeninhalt der Gesamtfigur ergibt sich aus der Addition der Flächeninhalte der Teilfiguren.
|
| |
Das ist ja klasse! Wir können feststellen, dass zwei Figuren den gleichen Flächeninhalt besitzen, obwohl wir den Flächeninhalt der einzelnen Teilflächen selbst noch gar nicht berechnen können! |
Hierzu ein kleines Beispiel:
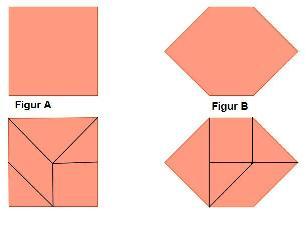
- Kannst Du zeigen, dass die beiden folgenden Figuren den gleichen Flächeninhalt haben?
Hier findest du den Hinweis
| |
Man kann die Berechnung des Flächeninhaltes von Figuren, für die man keine Berechnungsformel kennt, auf Figuren zurückführen, für die man eine Flächeninhaltsformel kennt. |
Zusammenfassung
- Übertrage folgende Definition in Dein Heft:
Zerlegungsgleichheit von Figuren Zwei Figuren sind zerlegungsgleich, wenn sie in paarweise kongruente Teilfiguren zerlegt werden können.
Beispiel:
Figur A und Figur B sind zerlegungsgleich. Zerlegungsgleiche Figuren besitzen den gleichen Flächeninhalt
Ergänzungsgleichheit von Figuren
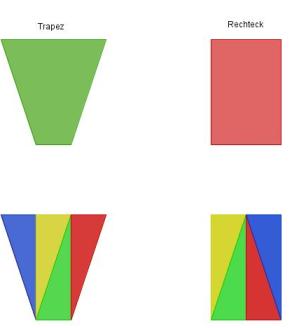
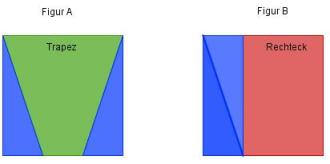
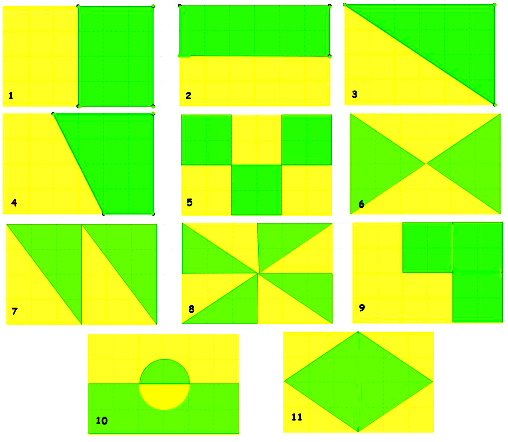
- Das Trapez und das Rechteck sind zerlegungsgleich, denn sie können z.B. in jeweils vier zueinander kongruente Dreiecke zerlegt werden.
- Man nennt dieses Rechteck und das Trapez aber auch ergänzungsgleich. Betrachte Dir dazu das nachfolgende Bild:
- Was bedeutet Ergänzungsgleichheit? Fülle dazu die Lücken aus:
Das Trapez und das Rechteck sind , das sie durch Ergänzung mit , in diesem Fall mit je zwei blauen Dreiecken in zueinander kongruente Figuren A und B überführt werden können.
kongruenten Teilfigurenergänzungsgleich
- Merke Dir folgende Definition zur Ergänzungsgleichheit:
|
|
Zwei Figuren sind ergänzungsgleich, wenn man sie durch Ergänzung mit kongruenten Teilfiguren in zerlegungsgleiche Figuren umwandeln kann. Ergänzungsgleiche Figuren sind daher auch zerlegungsgleich.Ergänzungsgleiche Figuren besitzen den gleichen Flächeninhalt. |
Vertiefen und Übung
Klassenzimmer streichen
- Eine Schulklasse hat sich entschieden die Rückwand des Klassenzimmers neu zu streichen. Da die Mädchen gelb und die Jungen grün streichen wollen, haben sie sich geeinigt die Rückwand jeweils in der Hälfte der Farben zu streichen.
- Hilf der Klasse bei den Designvorschlägen.
- Hier siehst Du die Rückwand des Klassenzimmers. Sie ist 4 Meter hoch und 6 Meter breit.
Wieviele Vorschläge hast Du? Übertage das Rechteck in Dein Heft und sei kreativ! Aber achte auch auf die Aufgabenstellung!
- Du findest hier ein paar Lösungsvorschläge:
Hast Du mehr Ideen gefunden?? Prima!
Aufgabenstellung:
Zeige, warum im Lösungsvorschlag 1, 3, 7 und 8 jeweils genau die Hälfte grün bzw. gelb gestrichen wird. Begründe mit dem, was Du bisher über Flächeninhalte gelernt hast.
[Lösung anzeigen]
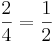wurde je die Hälfte grün bzw. gelb gefärbt.
