Weitere Abbildungen: Unterschied zwischen den Versionen
Aus DMUW-Wiki
(Die Seite wurde neu angelegt: <div style="float:right;background:#fff;margin-left:5px; padding:0px; border:1px solid #aaaaaa; width:16em"> <div style="font-size:100%; line-height:120%; padding: .5em...) |
(Struktur geändert) |
||
| (9 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | {{Vorlage:Abbildungen im Koordinatensystem}} | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
==Weitere Abbildungen== | ==Weitere Abbildungen== | ||
{| border="0" | {| border="0" | ||
! width="12" style="background-color:#D15FEE;"| | ! width="12" style="background-color:#D15FEE;"| | ||
| − | | width=" | + | | width="900" style="text-align:left"| '''Arbeitsauftrag''' |
-------- | -------- | ||
Es gibt noch weitere Abbildungen, die du bereits berechnen kannst,wie Orthogonale Affinität und Zentrische Strekung. Auch deren Abbildagleichungen sind noch einmal dargestellt. | Es gibt noch weitere Abbildungen, die du bereits berechnen kannst,wie Orthogonale Affinität und Zentrische Strekung. Auch deren Abbildagleichungen sind noch einmal dargestellt. | ||
|} | |} | ||
| + | <poem> | ||
{{#slideshare:weitereabbildungen-100609155242-phpapp01}} | {{#slideshare:weitereabbildungen-100609155242-phpapp01}} | ||
| − | + | Falls die Präsentation nicht geladen werden kann, kannst du sie auch als PDF anschauen. Einfach anklicken. | |
| − | <ggb_applet height=" | + | {{pdf|Peter Fischer_Weitere_Abbildungen.pdf|Weitere Abbildungen}} |
| + | |||
| + | |||
| + | Im folgenden GeoGebra-Applet kannst du dir nocheinmal die Zentrische Streckung mit ihren Eigenschaften erarbeiten. | ||
| + | <ggb_applet height="550" width="700" showMenuBar="false" showResetIcon="true" filename="Peter Fischer_Zentrische_Strekung.ggb" /> | ||
<span style="color:#FFFFFF"><big>Leerzeile</big></span> | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
| Zeile 36: | Zeile 23: | ||
==Aufgaben== | ==Aufgaben== | ||
| − | Es | + | Es folgen nun Teilaufgaben aus ehemaligen Abschlussprüfungen, die sich mit Abbildungen beschäftigen. |
{| border="1" | {| border="1" | ||
| − | ! width="12" style="background-color:# | + | ! width="12" style="background-color:#D15Fee;"| |
| − | | width=" | + | | width="900" style="text-align:left" style="background-color:#FFBBFF;"| '''Aufgabe 1 [[Bild:Peter_Fischer_Papier.png|40px]] ''' |
-------- | -------- | ||
| − | + | Funktionale Abhängigkeit aus der ebenen Geometrie. (Abschlussprüfung 2006; Wahlteil; A2 (verändert)). | |
| + | ------------ | ||
| + | Die gleichschenkligen Dreiecke <math>AB_nC_n \quad</math> bilden eine Dreiecksschar mit dem gemeinsamen Punkt <math>\quad A(0|0)</math>. Auf der Geraden g mit der Gleichung <math>\quad y=-2x+6</math> liegen die Mittelpunkte <math>\quad M_n(x|-2x+6)</math> der Hyptenusen <math>\quad[AB_n]</math>. | ||
|} | |} | ||
| − | |||
| − | {| | + | {| |
| − | | | + | |[[Bild:Peter_Fischer_Applet.png|35px|''Hier ist ein Applet zur anschaulichen Darstellung'']] |
| − | | | + | |<popup name="Applet zur anschaulichen Darstellung"> <ggb_applet height="570" width="700" showMenuBar="false" showResetIcon="true" filename="Peter Fischer_Gleichschenklig-Rechtwinklig.ggb"/> |
| − | + | </popup> | |
| − | | < | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
{| border="1" | {| border="1" | ||
| − | + | |Stellen Sie die Koordinaten der Punkte <math>\quad C_n</math> in Abhängigkeit der Abzisse x der Punkte <math>\quad M_n</math> dar. | |
| − | + | <popup name="Lösungshinweis"> <math>\vec{AM_n} \longrightarrow \vec{AM_n^*} \longrightarrow \vec{AC_n}</math> <math>\vec{AC_n}</math> Durch Drehung um <math> \quad A (0|0)</math> mit <math>\varphi=45^{\circ}</math> auf <math>\vec{AM_n^*} </math>, dann Zentrische Streckung um <math>\quad A(0|0)</math> mit <math>k=\sqrt{2}</math>.</popup> | |
| − | + | ||
| − | + | ||
| − | + | ||
<quiz display="simple"> | <quiz display="simple"> | ||
| − | { | + | { |
| type="{}" } | | type="{}" } | ||
| − | + | Lösung: <math>\quad C_n</math>=({ 3x-6 _7}|{ -x+6 _7}) (Auf ganze Zahlen runden) | |
| − | + | ||
| − | Lösung: <math>\quad | + | |
| − | + | ||
| − | + | ||
| − | + | ||
</quiz> | </quiz> | ||
| + | |} | ||
| Zeile 83: | Zeile 54: | ||
<poem> | <poem> | ||
<span style="color:#FFFFFF"><big>Leerzeile</big></span> | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
| − | '''Weiter gehts zu [[ | + | '''Weiter gehts zu [[../../Prüfungsaufgaben|Prüfungsaufgaben]]''' |
<span style="color:#FFFFFF"><big>Leerzeile</big></span> | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
</poem> | </poem> | ||
| Zeile 90: | Zeile 61: | ||
<div style="background:#D15FEE;text-align:center;color: #fff;font-weight:bold;font-size:125%;margin: 10px 5px 0px 0; padding: 4px 4px 4px 14px;">Abbildungen im Koordinatensystem</div> | <div style="background:#D15FEE;text-align:center;color: #fff;font-weight:bold;font-size:125%;margin: 10px 5px 0px 0; padding: 4px 4px 4px 14px;">Abbildungen im Koordinatensystem</div> | ||
<div style="margin: 0 5px 5px 0; padding: 1em 1em 1em 1em; text-align:center; border: 1px solid :#D15FEE; background-color:#f6fcfe;"> | <div style="margin: 0 5px 5px 0; padding: 1em 1em 1em 1em; text-align:center; border: 1px solid :#D15FEE; background-color:#f6fcfe;"> | ||
| − | [[LERNPFAD]] | [[Abbildungen im Koordinatensystem]] | [[Abbildung durch Drehung]] | [[Abbildung durch Achsenspiegelung]] | [[Weitere Abbildungen]] </div | + | [[../../|LERNPFAD]] | [[../|Abbildungen im Koordinatensystem]] | [[../Abbildung durch Drehung|Abbildung durch Drehung]] | [[../Abbildung durch Achsenspiegelung|Abbildung durch Achsenspiegelung]] | [[../Weitere Abbildungen|Weitere Abbildungen]] </div> |
Aktuelle Version vom 15. Oktober 2011, 12:10 Uhr
Weitere Abbildungen
| Arbeitsauftrag
Es gibt noch weitere Abbildungen, die du bereits berechnen kannst,wie Orthogonale Affinität und Zentrische Strekung. Auch deren Abbildagleichungen sind noch einmal dargestellt. |
{{#slideshare:weitereabbildungen-100609155242-phpapp01}}
Falls die Präsentation nicht geladen werden kann, kannst du sie auch als PDF anschauen. Einfach anklicken.
![]() Weitere Abbildungen
Weitere Abbildungen
Im folgenden GeoGebra-Applet kannst du dir nocheinmal die Zentrische Streckung mit ihren Eigenschaften erarbeiten.
Leerzeile
Aufgaben
Es folgen nun Teilaufgaben aus ehemaligen Abschlussprüfungen, die sich mit Abbildungen beschäftigen.
Stellen Sie die Koordinaten der Punkte 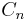 in Abhängigkeit der Abzisse x der Punkte in Abhängigkeit der Abzisse x der Punkte 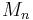 dar. dar.
|
Leerzeile
Weiter gehts zu Prüfungsaufgaben
Leerzeile
Abbildungen im Koordinatensystem
LERNPFAD | Abbildungen im Koordinatensystem | Abbildung durch Drehung | Abbildung durch Achsenspiegelung | Weitere Abbildungen
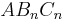 bilden eine Dreiecksschar mit dem gemeinsamen Punkt
bilden eine Dreiecksschar mit dem gemeinsamen Punkt 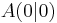 . Auf der Geraden g mit der Gleichung
. Auf der Geraden g mit der Gleichung 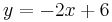 liegen die Mittelpunkte
liegen die Mittelpunkte 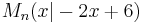 der Hyptenusen
der Hyptenusen ![\quad[AB_n]](/images/math/7/8/9/7897709debcde617572554254fb5973c.png) .
.
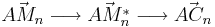
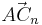 Durch Drehung um
Durch Drehung um 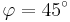 auf
auf 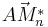 , dann Zentrische Streckung um
, dann Zentrische Streckung um 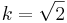 .
.
