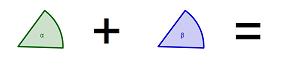Der Satz des Thales: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
K (→‎Beweisführung für den Satz des Thales!)
K (linkfix)
 
(38 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt)
Zeile 3: Zeile 3:
 
===Der Satz des Thales===
 
===Der Satz des Thales===
 
}}
 
}}
−
:'''Nach dem griechischen Philosophen und Mathematiker Thales von Milet (um 600 v. Chr.) wird ein wichtiger gemeotrischer Satz bezeichnet.'''<br>
 
−
<br>
 
−
<br>
 
 
<br>
 
<br>
 
<div style="border: 2px solid blue; background-color:#ffffff; padding:7px;">
 
<div style="border: 2px solid blue; background-color:#ffffff; padding:7px;">
−
===Betrachte aufmerksam die dynamische Animation!===
 
−
{|
 
−
|-
 
−
| <ggb_applet height="400" width="500" showResetIcon="true" filename="Animationthaleserscheint_nico.ggb" /> || '''Auf gehts - Löse das Quiz!'''
 
 
<br>
 
<br>
 +
: '''Nach dem griechischen Philosophen und Mathematiker Thales von Milet (um 600 v. Chr.) wird ein wichtiger gemeotrischer Satz bezeichnet.'''
 
<br>
 
<br>
−
'''Beziehe dich dabei auf die nebenstehende Animation.''' <br>
+
[[Bild: ThalesClownAAeinführung1_NicoStahl.jpg|thumb|center|500px|Ich bin der Thales-Clown]]
 
<br>
 
<br>
−
{|
+
: '''Du hast doch bei der Erarbeitung von Grundwissen verschiedene Winkel kennen gelernt, stimmts?'''
−
| <div class="schuettel-quiz"> <br>
+
−
Wenn die Strecke AB den '''Mittelpunkt''' M des Kreises schneidet, dann erscheint im Bild das Wort '''Thales'''.<br>
+
−
Weiterhin gilt dann auch, dass der Winkel an der Spitze C (grün markiert) '''rechtwinklig''' ist.<br>
+
−
Wenn das Dreieck ABC bei C ein Maß von 90° hat, so bezeichnet man die Strecke AB als '''Hypotenuse'''.<br>
+
−
Die beiden Strecken AC und BC nennt man '''Katheten'''.<br>
+
−
|</div>
+
−
|}
+
−
|}
+
−
</div>
+
 
<br>
 
<br>
 +
: '''Ich weiß also, dass du in der Lage bist einen spitzen von einem stumpfen Winkel zu unterscheiden!'''
 
<br>
 
<br>
 +
: '''Auf geht's - probiere doch bitte die erste Station aus - viel Spaß!!!'''
 
<br>
 
<br>
 +
: '''Die Lösung erhälst du, indem du die linke Maustaste gedrückt hältst und über den grauen Streifen ziehst.'''
 +
<br>
 +
===Erste Station:===
 
<br>
 
<br>
−
<br>
 
−
<div style="border: 2px solid blue; background-color:#ffffff; padding:7px;">
 
−
===Betrachte aufmerksam die dynamische Animation!===
 
 
{| {{Prettytable}}
 
{| {{Prettytable}}
 
|- style="background-color:#8DB6CD"
 
|- style="background-color:#8DB6CD"
−
| <ggb_applet height="400" width="400" showResetIcon="true" filename="Animationthaleseingeschalten.ggb" /> || <ggb_applet height="400" width="400" showResetIcon="true" filename="Animationthales.ggb" />
+
| <ggb_applet height="450" width="500" showResetIcon="true" filename="nico_stahlneugemachtwiderspruchsbeweisthales_nico.ggb" /> || <br>
−
|}
+
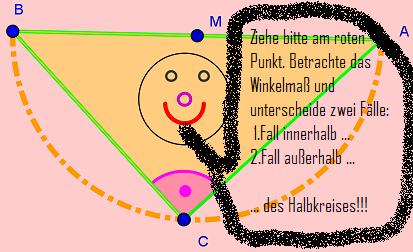
<br> !!!Ziehe am roten Punkt C. Beobachte dabei den Wert für den Winkel γ!!!
 
<br>
 
<br>
 
<br>
 
<br>
 +
* 1.Frage: Welchen Wert nimmt der Winkel γ an, wenn sich der rote Punkt C innerhalb des gelben Halbkreises befindet? 
 +
<br>
 +
* 1.Antwort: <u style="color:lightgrey;background:lightgrey">Der Winkel γ ist größer als 90°. Es gilt: γ > 90°</u>
 
<br>
 
<br>
−
===Versuche den Lückentext mithilfe der dynamischen Zeichnung zu lösen.===
+
* 2.Frage: Welchen Wert nimmt der Winkel γ an, wenn sich der rote Punkt C außerhalb des gelben Halbkreises befindet? (Jedoch innerhalb der blauen Linien und oberhalb der Strecke [AB]!) 
−
{|
+
−
| <div class="schuettel-quiz"> <br>
+
−
Wenn das Dreieck ABC bei dem Eckpunkt C '''rechtwinklig''' ist, dann liegt C auf dem Halbkreis über dem '''Durchmesser''' AB.<br>
+
−
Wenn der Punkt C auf dem Halbkreis über AB liegt, dann ist das '''Dreieck''' ABC rechtwinklig bei C.<br>
+
−
|</div>
+
−
|}<br>
+
−
''In der Mathematik kommt es häufig vor, dass Satz und Kehrsatz richtig sind.''<br>
+
−
''Anstelle von zwei Sätzen in Wenn-Dann-Form, wird die  Formulierung'' '''''"...genau dann, wenn..."''''' ''verwendet,''<br>
+
−
''sowohl um die Sätze zusammenzufassen als auch um die Korrektheit der Aussage zu artikulieren.''<br>
+
−
{|
+
−
| <div class="schuettel-quiz"> <br> Das Dreieck ABC hat genau dann bei C einen '''rechten''' Winkel, wenn die Ecke C auf dem '''Halbkreis''' über der Strecke AB liegt.<br>
+
−
|</div>
+
−
|}
+
−
</div>
+
 
<br>
 
<br>
 +
* 2.Antwort: <u style="color:lightgrey;background:lightgrey">Der Winkel γ ist kleiner als 90°. Es gilt: γ < 90°</u>
 
<br>
 
<br>
 +
* 3.Frage: Welchen Wert nimmt der Winkel γ an, wenn sich der rote Punkt C genau auf dem Halbkreis befindet?
 
<br>
 
<br>
 +
* 3.Antwort: <u style="color:lightgrey;background:lightgrey">Der Winkel γ beträgt dann genau 90°. Es gilt: γ = 90°</u>
 
<br>
 
<br>
 +
* 4.Frage: Welchen Wert nimmt der Winkel γ an, wenn du das Kästchen "Punkt fixieren" anklickst?
 
<br>
 
<br>
 +
* 4.Antwort: <u style="color:lightgrey;background:lightgrey">Der Winkel γ beträgt dann genau 90°. Es gilt: γ = 90°</u> <br>
 +
<br>
 +
Erklärung: <u style="color:lightgrey;background:lightgrey">Es gilt: γ = 90°, weil der rote Punkt C genau auf dem Halbreis über der Strecke [AB] liegt.</u> <br>
 +
|}
 +
</div>
 
<br>
 
<br>
 
<br>
 
<br>
 
<br>
 
<br>
 
<div style="border: 2px solid blue; background-color:#ffffff; padding:7px;">
 
<div style="border: 2px solid blue; background-color:#ffffff; padding:7px;">
−
===Ziehe am blauen Punkt C!===
 
−
{| {{Prettytable}}
 
−
|- style="background-color:#8DB6CD"
 
−
| <ggb_applet height="300" width="500" showResetIcon="true" filename="ThalesWERTE___nico_Nico.Stahl.ggb" /> || <ggb_applet height="300" width="500" showResetIcon="true" filename="ThalesWINKEL__Nico.Stahl.ggb" />
 
−
|}
 
 
<br>
 
<br>
−
<div class="zuordnungs-quiz"> <br>
+
[[Bild: ThalesClownSchieberegler_NicoStahl.jpg|thumb|center|500px|Ich bin der Thales-Clown]]  
−
<big>'''Aufgabenstellung: Ordne die untenstehenden Bilder und Begriffe passend zu!!!'''</big> <br>
+
−
{|
+
−
| Die Strecken [MA], [MB] und [MC] || sind alle gleich lang || werden mit r bezeichnet || sind der Radius des Kreises k || sind halb so lang wie der Durchmesser des Kreises k
+
−
|-
+
−
| Basiswinkel im Dreieck AMC || [[Bild:alpha_nicostahl.jpg|150px]]
+
−
|-
+
−
| [[Bild:beta_nicostahl.jpg|150px]] || Basiswinkel im Dreieck MBC
+
−
|-
+
−
| [[Bild:alpha+beta_istgleich_nicostahl.jpg|300px]] || [[Bild:GGamma___nicostahl.jpg|150px]] || [[Bild:GGammawinkel90°__nicostahl.jpg|150px]]
+
−
|}
+
 
<br>
 
<br>
−
</div>
+
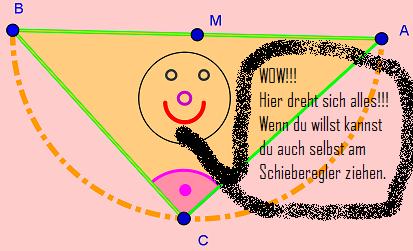
: '''Nachdem du die erste Station gemacht hast, kannst du dich jetzt der zweiten Station widmen!'''
 
<br>
 
<br>
 +
: '''Achte zunächst auf die linke Animation und beobachte den Winkel am roten Eckpunkt!
 
<br>
 
<br>
 +
: '''Wenn du damit fertig bist, dann schaue dir bitte dir rechte Animation an!'''
 
<br>
 
<br>
 +
: '''Was fällt dir auf, wenn du die Winkel betrachtest?'''
 
<br>
 
<br>
 +
: '''Wenn du willst kannst du die Animation auch stoppen, indem du auf den Pauseknopf (links unten im Applet) drückst!'''
 
<br>
 
<br>
 +
: '''Um die Fragen zu beantworten, nutze bitte den Multiple-Chpoice-Test!'''
 
<br>
 
<br>
 +
: '''Viel Spaß dabei!!!'''
 
<br>
 
<br>
 +
 +
===Zweite Station:===
 
<br>
 
<br>
 +
{| {{Prettytable}}
 +
|- style="background-color:#8DB6CD"
 +
| <ggb_applet height="400" width="400" showResetIcon="true" filename="OhneWinkelANIMATION_thales_nicostahl.ggb" /> || <ggb_applet height="400" width="400" showResetIcon="true" filename="ANIMATION_thales_nicostahl.ggb" />
 +
|}
 
<br>
 
<br>
 
<br>
 
<br>
 +
<big>'''Welche Aussagen über die dynamischen Animationen stimmen und welche nicht?'''</big>
 
<br>
 
<br>
 +
<div class="multiplechoice-quiz">
 +
 +
Der Winkel am roten Eckpunkt hat in der linken Animation eine andere Größe als in der rechten Animation. (Falsch) (!Richtig)
 +
 +
Der Winkel γ hat bei beiden Animationen stets ein Maß von 90°. (Richtig) (!Falsch)
 +
 +
Die beiden grünen Winkel sind nie gleich groß. (!Richtig) (Falsch)
 +
 +
Die Summe der beiden grünen Winkel ergibt stets das gleiche Ergebnis. (Richtig) (!Falsch)
 +
 +
Die Summe der beiden grünen Winkel ist so groß wie der Winkel γ. (Richtig) (!Falsch)
 +
 +
Wenn der Winkel γ nicht auf dem Kreis liegen würde, dann wäre das Winkelmaß entweder größer oder kleiner 90°. (Richtig) (!Falsch)
 +
 +
</div>
 
<br>
 
<br>
 
<br>
 
<br>
Zeile 123: Zeile 121:
 
<br>
 
<br>
 
<br>
 
<br>
 +
</div>
 
<br>
 
<br>
 
<br>
 
<br>
 
<br>
 
<br>
 +
<div style="border: 2px solid blue; background-color:#ffffff; padding:7px;">
 
<br>
 
<br>
−
</div>
+
[[Bild: MotivatorOrdnung_nicostahl.jpg|thumb|center|500px|Ich bin der Thales-Clown]]
 
<br>
 
<br>
−
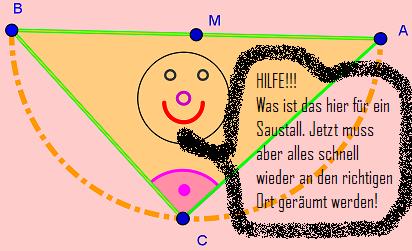
<div style="border: 2px solid blue; background-color:#ffffff; padding:7px;">
+
: '''Jetzt hast du einige Fragen beantortet und einen Multiple-Choice-Test erledigt!'''
 
<br>
 
<br>
−
===Beweisführung für den Satz des Thales!===
+
: '''Wie sieht's aus?'''
−
'''Klicke mit der linken Maustaste die einzelnen Schritte an.''' <br>
+
−
'''Wenn du möchtest kannst du am Punkt C mit der Maus ziehen.'''
+
 
<br>
 
<br>
 +
: '''Hast du ein bisschen Lust das Durcheinander hier aufzuräumen?'''
 
<br>
 
<br>
−
{|
+
: '''Wenn du willst, dann kannst du auch am blauen Punkt ziehen!'''
−
|-
+
<br>
−
| <ggb_applet height="500" width="650" showResetIcon="true" filename="BeweisführungdesThales_nico.ggb" /> || <div class="zuordnungs-quiz">
+
===Dritte Station:===
−
<big>'''Zuordnung'''</big><br>
+
<br>
−
Ordne den einzelnen Schritten die jeweils passenden Texte zu.
+
{| {{Prettytable}}
 +
|- style="background-color:#8DB6CD"
 +
| <ggb_applet height="300" width="500" showResetIcon="true" filename="ThalesWERTE___nico_Nico.Stahl.ggb" /> || <ggb_applet height="300" width="500" showResetIcon="true" filename="ThalesWINKEL__Nico.Stahl.ggb" />
 +
|}
 +
<br>
 +
<div class="zuordnungs-quiz"> <br>
 +
<big>'''Aufgabenstellung: Ordne die untenstehenden Bilder und Begriffe passend zu!!!'''</big> <br>
 
{|  
 
{|  
−
| Schritt 1 || Dreieck AMC und Dreieck MBC sind gleichschenklig. (r=r)   
+
| Die Strecken [MA], [MB] und [MC] || sind alle gleich lang || werden mit r bezeichnet || sind der Radius des Kreises k || sind halb so lang wie der Durchmesser des Kreises k
 
|-
 
|-
−
| Schritt 2 || Basiswinkel sind maßgleich: α = α 
+
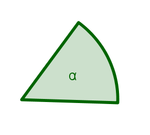
| Basiswinkel im Dreieck AMC || [[Bild:alpha_nicostahl.jpg|150px]]
 
|-
 
|-
−
| Schritt 3 || Basiswinkel sind maßgleich: β = β 
+
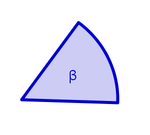
| [[Bild:beta_nicostahl.jpg|150px]] || Basiswinkel im Dreieck MBC
 
|-
 
|-
−
| Schritt 4 || Innenwinkelsumme im Dreieck ABC=180°: <br>
+
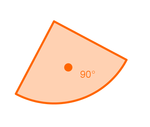
| [[Bild:alpha+beta_istgleich_nicostahl.jpg|300px]] || [[Bild:GGamma___nicostahl.jpg|150px]] || [[Bild:GGammawinkel90°__nicostahl.jpg|150px]]
−
α + α + β + β = 180° <br>
+
−
2α +  2β = 180° <br>
+
−
α + β = 90° <br>
+
−
|-
+
−
| Schritt 5 || α + β = γ <br> γ = 90°
+
 
|}
 
|}
 
<br>
 
<br>
 
</div>
 
</div>
 
<br>
 
<br>
−
|}
 
 
<br>
 
<br>
−
</div>
 
 
<br>
 
<br>
 
<br>
 
<br>
−
<div style="border: 2px solid blue; background-color:#ffffff; padding:7px;">
 
−
<div style="padding:10px;background:#ffffff;border:1px ;">
 
−
 
−
===Auf gehts - löse den Lückentext:===
 
−
'''Fülle die Lücken, indem du die passenden Begriffe zu den Feldern ziehst (mit der linken Maustaste zur Lücke ziehen und fallenlassen).'''
 
−
<div class="lueckentext-quiz">
 
 
<br>
 
<br>
−
Wir wollen diesen Sachverhalt nun mathematisch untersuchen und dazu gehen wir davon aus,<br>
 
−
dass das in der Zeichnung ersichtliche Dreieck einen <strong> rechten </strong> Winkel bei C aufzeigt.<br>
 
−
Also sind die <strong> Punkte A, B und C </strong> gleich weit von <strong> M </strong> entfernt,<br>
 
−
liegen somit auf dem <strong> Kreis </strong> um M,<br>
 
−
der zugleich <strong> Mittelpunkt </strong> von der <strong> Strecke AB </strong> ist. <br>
 
−
Das heißt, wenn das <strong> Dreieck ABC </strong> bei der <strong> Ecke C </strong> rechtwinklig ist, <br>
 
−
dann liegt C auf dem <strong> Halbkreis </strong> über der Strecke AB. <br>
 
−
Die Strecke AB ist zudem auch der <strong> Durchmesser </strong> des <strong> THALES-KREISES </strong>.<br>                           
 
−
</div>
 
 
<br>
 
<br>
−
</div>
 
 
<br>
 
<br>
 
<br>
 
<br>
Zeile 199: Zeile 181:
 
<br>
 
<br>
 
<br>
 
<br>
−
</div>
 
 
<br>
 
<br>
 
<br>
 
<br>
−
<div style="border: 2px solid blue; background-color:#ffffff; padding:7px;">
 
−
{| {{Prettytable}}
 
−
|- style="background-color:#8DB6CD"
 
−
| <ggb_applet height="450" width="500" showResetIcon="true" filename="widerspruchsbeweisthales_nico.ggb" /> || <br>
 
−
<br> !!!Ziehe am roten Punkt C. Beobachte dabei den Wert für den Winkel γ!!!
 
 
<br>
 
<br>
 
<br>
 
<br>
−
* 1.Frage: Welchen Wert nimmt der Winkel γ an, wenn sich der rote Punkt C innerhalb des gelben Halbkreises befindet? 
 
−
<br>
 
−
* 1.Antwort: <u style="color:lightgrey;background:lightgrey">Der Winkel γ ist größer als 90°. Es gilt: γ > 90°</u>
 
 
<br>
 
<br>
−
* 2.Frage: Welchen Wert nimmt der Winkel γ an, wenn sich der rote Punkt C außerhalb des gelben Halbkreises befindet? (Jedoch innerhalb der blauen Linien?) 
 
 
<br>
 
<br>
−
* 2.Antwort: <u style="color:lightgrey;background:lightgrey">Der Winkel γ ist kleiner als 90°. Es gilt: γ < 90°</u>
 
 
<br>
 
<br>
−
* 3.Frage: Welchen Wert nimmt der Winkel γ an, wenn sich der rote Punkt C genau auf dem Halbkreis befindet?
 
 
<br>
 
<br>
−
* 3.Antwort: <u style="color:lightgrey;background:lightgrey">Der Winkel γ beträgt dann genau 90°. Es gilt: γ = 90°</u>
 
 
<br>
 
<br>
−
* 4.Frage: Welchen Wert nimmt der Winkel γ an, wenn du das Kästchen "Punkt fixieren" anklickst?
 
 
<br>
 
<br>
−
* 4.Antwort: <u style="color:lightgrey;background:lightgrey">Der Winkel γ beträgt dann genau 90°. Es gilt: γ = 90°</u> <br>
 
 
<br>
 
<br>
−
Erklärung: <u style="color:lightgrey;background:lightgrey">Es gilt: γ = 90°, weil der rote Punkt C genau auf dem Halbreis über der Strecke [AB] liegt.</u> <br>
+
<br>
−
|}
+
<br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 
</div>
 
</div>
 
<br>
 
<br>
Zeile 232: Zeile 206:
 
<br>
 
<br>
 
<br>
 
<br>
−
<div style="border: 2px solid red; background-color:#ffffff; padding:7px;"> <br>
+
<div style="border: 2px solid blue; background-color:#ffffff; padding:7px;">
−
 
+
−
===Viel Spaß beim Multiple-Choice!===
+
 
<br>
 
<br>
−
'''''Beziehe dich bei der Beantwortung der Aufgaben auf die nebenstehende Zeichnungen!!!'''''
+
[[Bild: ThalesClowntippschieberegler_NicoStahl.jpg|thumb|center|500px|Ich bin der Thales-Clown]]
 
<br>
 
<br>
−
{|
+
: '''Was bemerkst du beim Winkel γ, wenn der blaue Punkt B so wandert, dass die Strecke [AB] den Mittelpunkt M schneidet?'''
−
| <quiz display="simple">
+
<br>
−
{ '''Welche Aussagen über die Winkel α und β sind wahr?'''}
+
: '''Betrachte aufmerksam die dynamische Animation!'''
−
 
+
<br>
−
- Die Summe aus den Winkeln α + β ergeben zusammen immer 60°.
+
: '''Auf geht's - viel Spaß beim Ordnen der durchgeschüttelten Wörter!'''
−
+ Die Summe der beiden Winkel α + β ist immer gleich.
+
<br>
−
+ Das Maß des Winkels γ an der Spitze C berechnet sich aus der Summe der Winkel α + β.
+
: '''Keine Angst - Du kennst die gesuchten Wörter - Du schaffst das auf jeden Fall!!!'''
−
- Der Winkel β kann nie doppelt so groß sein wie der Winkel α.
+
<br>
−
- Der Winkel α misst immer 90°.
+
===Vierte Station:===
−
- Der Winkel β misst immer 90°.
+
<br>
−
+ Falls gilt: α = 45°, so folgt: α = β.
+
{| {{Prettytable}}
−
- Die beiden Winkel α und β sind nie maßgleich.
+
|- style="background-color:#8DB6CD"
−
 
+
| <ggb_applet height="500" width="550" showResetIcon="true" filename="stumpf_nico_stahl_Animationthaleserscheint_nico.ggb" /> || {|
−
{ '''Welche Aussagen über den Winkel γ sind wahr?'''}
+
| <div class="schuettel-quiz"> <br>
−
 
+
Wenn die Strecke [AB] den '''Mittelpunkt''' M des Kreises schneidet,
−
+ Der Winkel γ misst immer 90°.
+
−
- Der Winkel γ misst nie 90°.
+
−
- Für den Winkel γ gilt: γ < 90°.
+
−
- Für den Winkel γ gilt: γ > 90°.
+
−
+ Für den Winekl γ gilt: γ = 90°.
+
 
<br>  
 
<br>  
−
</quiz> || <ggb_applet height="350" width="610" showResetIcon="true" filename="KreuzwortThales_nicostahl.ggb" /> <br> <br> <ggb_applet height="350" width="610" showResetIcon="true" filename="ThalesKreuz_Nico.Stahl.ggb" />
+
dann ist der Winkel an der Spitze C '''rechtwinklig'''
−
|}
+
−
</div>
+
 
<br>
 
<br>
 +
und im Bild erscheint das Wort: '''Thales'''.
 
<br>
 
<br>
 +
Wenn das Dreieck ABC bei C ein Maß von 90° hat,
 
<br>
 
<br>
−
<div style="border: 2px solid yellow; background-color:#ffffff; padding:7px;">
+
so bezeichnet man die Strecke [AB] als '''Hypotenuse'''.
−
{{Merke|'''Der Satz des Thales:''' <br>
+
 
<br>
 
<br>
−
'''''Jedes Dreieck ∆ABC, dessen Grundseite AB dem Durchmesser eines Halbkreises entspricht und dessen Ecke C auf dem Kreisbogen liegt,'''''<br>
+
Die beiden Strecken [AC] und [BC] nennt man '''Katheten'''.
−
'''''ist rechtwinklig. Den Halbkreis mit dem eingeschlossenen Dreieck bezeichnet man kurz als „Thales-Kreis“.'''''}} <br>
+
<br>
 +
|</div>
 +
|}
 
</div>
 
</div>
 +
<br>
 
<br>
 
<br>
 
<br>
 
<br>
 
<br>
 
<br>
 
<div style="border: 2px solid blue; background-color:#ffffff; padding:7px;">
 
<div style="border: 2px solid blue; background-color:#ffffff; padding:7px;">
−
'''Hier findest du Wörter, die du beim Bearbeiten des Lernpfades kennengelernt hast.''' <br>
+
<br>
−
'''Waagrecht und senkrecht, gefundene Wörter werden grün markiert.'''<div class="suchsel-quiz">
+
[[Bild: ThalesClownBEWEISCLOWN_NicoStahl.jpg|thumb|center|500px|Ich bin der Thales-Clown]]
−
{|
+
<br>
−
|Hypotenuse
+
 
 +
===Fünfte Station:===
 +
<br>
 +
: '''Hast du Lust auf eine Beweisführung?'''
 +
<br>
 +
: '''Klicke mit der linken Maustaste die einzelnen Schritte an!'''
 +
<br>
 +
: '''Auf geht's - viel Spaß beim Zuordnen der Begriffe!'''
 +
<br>
 +
: '''Wenn du möchtest kannst du am Punkt C mit der Maus ziehen.'''
 +
<br>
 +
<br>
 +
{|{{Prettytable}}
 +
|- style="background-color:#8DB6CD"
 +
| <ggb_applet height="500" width="650" showResetIcon="true" filename="BeweisführungdesThales_nico.ggb" /> || <div class="zuordnungs-quiz">
 +
<big>'''Zuordnung'''</big><br>
 +
Ordne den einzelnen Schritten den jeweils passenden Text zu.
 +
{|  
 +
| Schritt 1 || Dreieck AMC und Dreieck MBC sind gleichschenklig. (r=r)   
 
|-
 
|-
−
|Dreieck
+
| Schritt 2 || Basiswinkel im Dreieck AMC sind maßgleich: α = α 
 
|-
 
|-
−
|rechtwinklig
+
| Schritt 3 || Basiswinkel im Dreieck MBC sind maßgleich: β = β 
 
|-
 
|-
−
|Thalessatz
+
| Schritt 4 || Innenwinkelsumme im Dreieck ABC=180°: <br>
 +
α + α + β + β = 180° <br>
 +
2α +  2β = 180° <br>
 +
α + β = 90° <br>
 
|-
 
|-
−
|Durchmesser
+
| Schritt 5 || α + β = γ <br> γ = 90°
−
|-
+
−
|Radius
+
−
|-
+
−
|Kathete
+
−
|-
+
−
|Basiswinkel
+
−
|-
+
−
|gleichschenklig
+
−
|-
+
−
|Innenwinkelsumme
+
−
|-
+
−
|Seitenhalbierende
+
−
|-
+
−
|Kongruenz
+
−
|-
+
−
|Halbkreis
+
−
|-
+
−
|Kreis
+
−
|-
+
−
|Basisseite
+
−
|-
+
−
|spitzwinklig
+
−
|-
+
−
|stumpfwinklig
+
 
|}
 
|}
 +
<br>
 
</div>
 
</div>
 
<br>
 
<br>
 +
|}
 
<br>
 
<br>
 +
</div>
 
<br>
 
<br>
 
<br>
 
<br>
 
<br>
 
<br>
 +
<div style="border: 2px solid blue; background-color:#ffffff; padding:7px;">
 
<br>
 
<br>
 +
[[Bild: ThalesClownPro_NicoStahl.jpg|thumb|center|500px|Ich bin der Thales-Clown]] <br>
 
<br>
 
<br>
 +
===Sechste Station:===
 
<br>
 
<br>
 +
: '''Du hast mittlerweile schon viele neue Entdeckungen gemacht!'''
 
<br>
 
<br>
 +
: '''Wende nun diese gewonnenen Erkenntnisse auf den nachfolgenden Lückentext an!'''
 
<br>
 
<br>
 +
{|
 +
| <div class="schuettel-quiz"> <br>
 +
Wenn das Dreieck ABC bei dem Eckpunkt C '''rechtwinklig''' ist, dann liegt C auf dem Halbkreis über dem '''Durchmesser''' AB.<br>
 +
Wenn der Punkt C auf dem Halbkreis über AB liegt, dann ist das '''Dreieck''' ABC rechtwinklig bei C.<br>
 +
|</div>
 +
|}<br>
 +
''In der Mathematik kommt es häufig vor, dass Satz und Kehrsatz richtig sind.''<br>
 +
''Anstelle von zwei Sätzen in Wenn-Dann-Form, wird die  Formulierung'' '''''"...genau dann, wenn..."''''' ''verwendet,''<br>
 +
''sowohl um die Sätze zusammenzufassen als auch um die Korrektheit der Aussage zu artikulieren.''<br>
 +
{|
 +
| <div class="schuettel-quiz"> <br> Das Dreieck ABC hat genau dann bei C einen '''rechten''' Winkel, wenn die Ecke C auf dem '''Halbkreis''' über der Strecke AB liegt.<br>
 +
|</div>
 +
|}
 +
</div>
 
<br>
 
<br>
 
<br>
 
<br>
 +
<div style="border: 2px solid yellow; background-color:#ffffff; padding:7px;">
 
<br>
 
<br>
 +
[[Bild: Hefteintag.ThalesClown_nicostahl.jpg|thumb|center|500px|Ich bin der Thales-Clown]]
 
<br>
 
<br>
 +
: '''Es wird wieder Zeit unser neues Wissen zusammen zu tragen!'''
 
<br>
 
<br>
 +
: '''Übertrage den Merk-Text in dein Arbeitsheft!'''
 
<br>
 
<br>
 +
{{Merke|'''Der Satz des Thales:'''
 
<br>
 
<br>
 
<br>
 
<br>
 +
* '''Wenn das Dreieck ABC bei dem Eckpunkt C rechtwinklig ist, dann liegt C auf dem Halbkreis über dem Durchmesser AB.'''
 
<br>
 
<br>
 +
* '''Wenn der Punkt C auf dem Halbkreis über AB liegt, dann ist das Dreieck ABC rechtwinklig bei C.'''
 
<br>
 
<br>
 +
* '''Das Dreieck ABC hat genau dann bei C einen rechten Winkel, wenn die Ecke C auf dem Halbkreis über der Strecke AB liegt.
 +
}} <br>
 +
</div>
 
<br>
 
<br>
 +
<div style="border: 2px solid green; background-color:#ffffff; padding:7px;">
 
<br>
 
<br>
 +
[[Bild: ThalesClownbeweisnr2thales_NicoStahl.jpg|thumb|center|500px|Ich bin der Thales-Clown]]
 
<br>
 
<br>
 
<br>
 
<br>
 +
===Siebte Station:===
 
<br>
 
<br>
 +
: '''Super, du hast die fünfte und die sechste Station geschafft!'''
 
<br>
 
<br>
 +
: '''Dann wird die siebte Station dür dich "very easy"!!!'''
 
<br>
 
<br>
 +
: '''Auf geht's - viel Spaß beim Zuordnen der Begriffe!'''
 
<br>
 
<br>
 +
: '''Wenn du willst, dann kannst du auch am blauen Punkt C ziehen!'''
 
<br>
 
<br>
 +
{| {{Prettytable}}
 +
|- style="background-color:#8DB6CD"
 +
| <ggb_applet height="600" width="550" showResetIcon="true" filename="beweisnummer2thales_nicostahl.ggb" /> || <div class="zuordnungs-quiz">
 +
<big>'''Zuordnung'''</big>
 
<br>
 
<br>
 +
{|
 +
| Schritt 1 || Gerade g ist parallel zu Strecke [AB]
 +
|-
 +
| Schritt 2 || Dreieck AMC und Dreieck CMB sind gleichschenklig
 +
|-
 +
| Schritt 3 || [MA]=[MB]=[MC]: r=r=r
 +
|-
 +
| Schritt 4 || Basiswinkel sind gleich groß: α=α und β=β
 +
|-
 +
| Schritt 5 || Innenwinkelsumme im Dreieck: <br> α+β+γ=180° <br> α+β=γ <br> α+β+α+β=180° <br> 2α+2β=180° <br> α+β=90° <br>
 +
|-
 +
| Schritt 6 || Wechselwinkel an parallelen Geraden sind gleich groß: α=α und β=β
 +
|-
 +
| Schritt 7 || Nebenwinkel ergänzen sich zu 180°: <br> α+α+β+β=180° <br> 2α+2β=180° <br> α+β=90° <br> γ=90° <br>
 +
|}
 +
</div>
 +
<br>
 +
|}
 
<br>
 
<br>
 
<br>
 
<br>
Zeile 354: Zeile 381:
 
<br>
 
<br>
 
</div>
 
</div>
 +
<br>
 +
<br>
 
<br>
 
<br>
 
<div style="border: 2px solid red; background-color:#ffffff; padding:7px;">
 
<div style="border: 2px solid red; background-color:#ffffff; padding:7px;">
 +
<br>
 +
[[Bild:ThalesClownSTolz_NicoStahl.jpg|thumb|center|500px|Ich bin der Thales-Clown]]
 +
<br>
 +
: '''Eigentlich, müsstest du jetzt doch alles verstanden haben, oder?'''
 +
<br>
 +
: '''Die nachstehenden Aufgaben kannst du in Absprache mit deinem Lehrer oder deiner Lehrerin bearbeiten!'''
 +
<br>
 
{{Aufgabe-Mathe|'''Arbeitsauftrag: <br>
 
{{Aufgabe-Mathe|'''Arbeitsauftrag: <br>
 
* Konstruiere in dein Übungsheft einen Thales-Kreis.<br>
 
* Konstruiere in dein Übungsheft einen Thales-Kreis.<br>

Aktuelle Version vom 4. März 2012, 23:34 Uhr


Mathematik-digital Pfeil-3d.png
Lernpfad

Der Satz des Thales



Nach dem griechischen Philosophen und Mathematiker Thales von Milet (um 600 v. Chr.) wird ein wichtiger gemeotrischer Satz bezeichnet.


Ich bin der Thales-Clown


Du hast doch bei der Erarbeitung von Grundwissen verschiedene Winkel kennen gelernt, stimmts?


Ich weiß also, dass du in der Lage bist einen spitzen von einem stumpfen Winkel zu unterscheiden!


Auf geht's - probiere doch bitte die erste Station aus - viel Spaß!!!


Die Lösung erhälst du, indem du die linke Maustaste gedrückt hältst und über den grauen Streifen ziehst.


Erste Station:


 !!!Ziehe am roten Punkt C. Beobachte dabei den Wert für den Winkel γ!!!

  • 1.Frage: Welchen Wert nimmt der Winkel γ an, wenn sich der rote Punkt C innerhalb des gelben Halbkreises befindet?


  • 1.Antwort: Der Winkel γ ist größer als 90°. Es gilt: γ > 90°


  • 2.Frage: Welchen Wert nimmt der Winkel γ an, wenn sich der rote Punkt C außerhalb des gelben Halbkreises befindet? (Jedoch innerhalb der blauen Linien und oberhalb der Strecke [AB]!)


  • 2.Antwort: Der Winkel γ ist kleiner als 90°. Es gilt: γ < 90°


  • 3.Frage: Welchen Wert nimmt der Winkel γ an, wenn sich der rote Punkt C genau auf dem Halbkreis befindet?


  • 3.Antwort: Der Winkel γ beträgt dann genau 90°. Es gilt: γ = 90°


  • 4.Frage: Welchen Wert nimmt der Winkel γ an, wenn du das Kästchen "Punkt fixieren" anklickst?


  • 4.Antwort: Der Winkel γ beträgt dann genau 90°. Es gilt: γ = 90°


Erklärung: Es gilt: γ = 90°, weil der rote Punkt C genau auf dem Halbreis über der Strecke [AB] liegt.





Ich bin der Thales-Clown


Nachdem du die erste Station gemacht hast, kannst du dich jetzt der zweiten Station widmen!


Achte zunächst auf die linke Animation und beobachte den Winkel am roten Eckpunkt!


Wenn du damit fertig bist, dann schaue dir bitte dir rechte Animation an!


Was fällt dir auf, wenn du die Winkel betrachtest?


Wenn du willst kannst du die Animation auch stoppen, indem du auf den Pauseknopf (links unten im Applet) drückst!


Um die Fragen zu beantworten, nutze bitte den Multiple-Chpoice-Test!


Viel Spaß dabei!!!


Zweite Station:



Welche Aussagen über die dynamischen Animationen stimmen und welche nicht?

Der Winkel am roten Eckpunkt hat in der linken Animation eine andere Größe als in der rechten Animation. (Falsch) (!Richtig)

Der Winkel γ hat bei beiden Animationen stets ein Maß von 90°. (Richtig) (!Falsch)

Die beiden grünen Winkel sind nie gleich groß. (!Richtig) (Falsch)

Die Summe der beiden grünen Winkel ergibt stets das gleiche Ergebnis. (Richtig) (!Falsch)

Die Summe der beiden grünen Winkel ist so groß wie der Winkel γ. (Richtig) (!Falsch)

Wenn der Winkel γ nicht auf dem Kreis liegen würde, dann wäre das Winkelmaß entweder größer oder kleiner 90°. (Richtig) (!Falsch)


































Ich bin der Thales-Clown


Jetzt hast du einige Fragen beantortet und einen Multiple-Choice-Test erledigt!


Wie sieht's aus?


Hast du ein bisschen Lust das Durcheinander hier aufzuräumen?


Wenn du willst, dann kannst du auch am blauen Punkt ziehen!


Dritte Station:



Aufgabenstellung: Ordne die untenstehenden Bilder und Begriffe passend zu!!!

Die Strecken [MA], [MB] und [MC] sind alle gleich lang werden mit r bezeichnet sind der Radius des Kreises k sind halb so lang wie der Durchmesser des Kreises k
Basiswinkel im Dreieck AMC Alpha nicostahl.jpg
Beta nicostahl.jpg Basiswinkel im Dreieck MBC
Alpha+beta istgleich nicostahl.jpg GGamma nicostahl.jpg GGammawinkel90° nicostahl.jpg



















































Ich bin der Thales-Clown


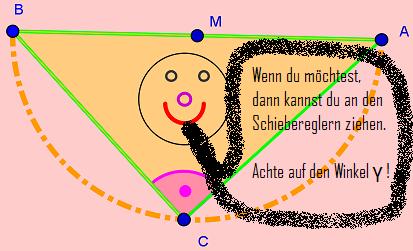
Was bemerkst du beim Winkel γ, wenn der blaue Punkt B so wandert, dass die Strecke [AB] den Mittelpunkt M schneidet?


Betrachte aufmerksam die dynamische Animation!


Auf geht's - viel Spaß beim Ordnen der durchgeschüttelten Wörter!


Keine Angst - Du kennst die gesuchten Wörter - Du schaffst das auf jeden Fall!!!


Vierte Station:

Wenn die Strecke [AB] den Mittelpunkt M des Kreises schneidet,
dann ist der Winkel an der Spitze C rechtwinklig
und im Bild erscheint das Wort: Thales.
Wenn das Dreieck ABC bei C ein Maß von 90° hat,
so bezeichnet man die Strecke [AB] als Hypotenuse.
Die beiden Strecken [AC] und [BC] nennt man Katheten.






Ich bin der Thales-Clown


Fünfte Station:


Hast du Lust auf eine Beweisführung?


Klicke mit der linken Maustaste die einzelnen Schritte an!


Auf geht's - viel Spaß beim Zuordnen der Begriffe!


Wenn du möchtest kannst du am Punkt C mit der Maus ziehen.



Zuordnung
Ordne den einzelnen Schritten den jeweils passenden Text zu.

Schritt 1 Dreieck AMC und Dreieck MBC sind gleichschenklig. (r=r)
Schritt 2 Basiswinkel im Dreieck AMC sind maßgleich: α = α
Schritt 3 Basiswinkel im Dreieck MBC sind maßgleich: β = β
Schritt 4 Innenwinkelsumme im Dreieck ABC=180°:

α + α + β + β = 180°
2α + 2β = 180°
α + β = 90°

Schritt 5 α + β = γ
γ = 90°








Ich bin der Thales-Clown


Sechste Station:


Du hast mittlerweile schon viele neue Entdeckungen gemacht!


Wende nun diese gewonnenen Erkenntnisse auf den nachfolgenden Lückentext an!



Wenn das Dreieck ABC bei dem Eckpunkt C rechtwinklig ist, dann liegt C auf dem Halbkreis über dem Durchmesser AB.
Wenn der Punkt C auf dem Halbkreis über AB liegt, dann ist das Dreieck ABC rechtwinklig bei C.

In der Mathematik kommt es häufig vor, dass Satz und Kehrsatz richtig sind.
Anstelle von zwei Sätzen in Wenn-Dann-Form, wird die Formulierung "...genau dann, wenn..." verwendet,
sowohl um die Sätze zusammenzufassen als auch um die Korrektheit der Aussage zu artikulieren.


Das Dreieck ABC hat genau dann bei C einen rechten Winkel, wenn die Ecke C auf dem Halbkreis über der Strecke AB liegt.




Ich bin der Thales-Clown


Es wird wieder Zeit unser neues Wissen zusammen zu tragen!


Übertrage den Merk-Text in dein Arbeitsheft!


Nuvola apps kig.png   Merke

Der Satz des Thales:

  • Wenn das Dreieck ABC bei dem Eckpunkt C rechtwinklig ist, dann liegt C auf dem Halbkreis über dem Durchmesser AB.


  • Wenn der Punkt C auf dem Halbkreis über AB liegt, dann ist das Dreieck ABC rechtwinklig bei C.


  • Das Dreieck ABC hat genau dann bei C einen rechten Winkel, wenn die Ecke C auf dem Halbkreis über der Strecke AB liegt.



Ich bin der Thales-Clown



Siebte Station:


Super, du hast die fünfte und die sechste Station geschafft!


Dann wird die siebte Station dür dich "very easy"!!!


Auf geht's - viel Spaß beim Zuordnen der Begriffe!


Wenn du willst, dann kannst du auch am blauen Punkt C ziehen!


Zuordnung

Schritt 1 Gerade g ist parallel zu Strecke [AB]
Schritt 2 Dreieck AMC und Dreieck CMB sind gleichschenklig
Schritt 3 [MA]=[MB]=[MC]: r=r=r
Schritt 4 Basiswinkel sind gleich groß: α=α und β=β
Schritt 5 Innenwinkelsumme im Dreieck:
α+β+γ=180°
α+β=γ
α+β+α+β=180°
2α+2β=180°
α+β=90°
Schritt 6 Wechselwinkel an parallelen Geraden sind gleich groß: α=α und β=β
Schritt 7 Nebenwinkel ergänzen sich zu 180°:
α+α+β+β=180°
2α+2β=180°
α+β=90°
γ=90°
















Ich bin der Thales-Clown


Eigentlich, müsstest du jetzt doch alles verstanden haben, oder?


Die nachstehenden Aufgaben kannst du in Absprache mit deinem Lehrer oder deiner Lehrerin bearbeiten!


  Aufgabe   Stift.gif

Arbeitsauftrag:

  • Konstruiere in dein Übungsheft einen Thales-Kreis.
  • Schreibe die besonderen Eigenschaften eines Thales-Kreis in dein Heft.
  • Füge sonstige Besonderheiten hinzu, die dir während des Bearbeitens des Lernpfades aufgefallen sind.
  • Diskutiere in deiner Klassengemeinschaft über diesen Lernpfad



Team.gif
Entstanden unter Mitwirkung von:

Nico Stahl

Von „http://dmuw.zum.de/index.php?title=Lernpfade/Satz_des_Thales/Der_Satz_des_Thales&oldid=30959“