Simon Möckl: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: 1. Aufgabe <ggb_applet width="1280" height="648" version="3.2" ggbBase64="UEsDBBQACAAIAAep6TwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1srVXBbtswDD2vXyH4tGFoYydN0QJxi627FOi2...)
 
K (hat „Benutzer:Simon Moeckl“ nach „Mathematisches Praktikum SS2010/Simon Möckl“ verschoben: Unterseite)
 
(11 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
−
1. Aufgabe
+
1. Aufgabe<br />
  
−
<ggb_applet width="1280" height="648"  version="3.2" ggbBase64="UEsDBBQACAAIAAep6TwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1srVXBbtswDD2vXyH4tGFoYydN0QJxi627FOi2Q7Zi20226USrLBmSnDr9+pGUnQTZBvTQkyWKeSQfH5nFTd9osQHnlTV5kp2liQBT2kqZVZ50oT69TG6uTxYrsCsonBS1dY0MeTI7myZk79T1yZuFX9snITW7PCh4ypPgOkiEbx3Iyq8BQjTXUnu0y65XWkm3/Vr8hjL4/UPEuDNtF0aQsqnulR+vE47XahU+qY2qwAltyzy5mGPmeHoAF1QpdZ6cp9EyzZPp0SOaZvS6tk49WxPIfQ9eo0UIr54BCZmSbTHhOhfQlVpVShoqhvNAJyGeVBXW6JtOzxET1GqNyV6cX0S40lpXLbc+QCP6X+As5pPNiehtvM3izWNiGHGe8tPhjWFgs4QQsC1eyB78SM7KqWrHHl3u/Eer96bWKhNuZRs6xy2dDaZl2BI+hnKU7wez0jDYpkj5GsrHwvbLSMIsQn/btvwTzqdY3VptnXBE7xwdhm8Rv+xDie68UvZJ2WPAINDde3Y1ZQ/+FvHLXlqZmNpQeDZWnaVjGOUFGYhFVOLIjZYFYGcT0RkV7scLKuBxqDSL/l+6psAJONTADjJ7NUjKWVQo5B+Y6BkyReef8cwaO1LX4hGcAR0lZLDzne282JBWY28ZtYJSNXiNDwNjkrr5HTOM1gpWDsbC4oBFPvk1PZTpkXkxGZOgHDwWUwZcFFhwoGJpkAMOEZ0qGchCU6KhARyhwHIxXQNOlTvqZELRMEQ3BhoVzkvE8kI4ontPIj7/R1C4Otq1JLhskI3c4nI4LJHRPttqCDz4ec1bpFG4/04znr5G9qQuOsrCW90FWJZIobm3pQy8KWN+u8ln356WziWPb55cXdGhVj3sh/Hf+2av77BGIRnwnocwHI6bNNhm5h4XSTtsat8CofN59BYtFs6jvlMJSiu2hJrT40r2tO1Hcmvc+D0i1m/7dyIXCCYmohfvhUzE5K921p1hCST7n7+4htdqcPrCBqcv5veQocmh0nn3D/99138AUEsHCGTqtPX9AgAALQcAAFBLAQIUABQACAAIAAep6Txk6rT1/QIAAC0HAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAANwMAAAAA" framePossible = "true" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" />
+
Gegeben ist die Funktion <math>f(x)=\frac{1}{x} + a</math>, <math>x \in R \setminus \{ 0\} </math>, <math>a\in[-10;10]</math>.<br />
 +
a ist dabei der Parameter, der durch den Schieberegler verändert werden kann.<br />
 +
Den Schieberegler kannst du bedienen, indem du einfach mit gedrückter Maustaste auf dem Punkt die Maus nach links bzw. rechts ziehst.<br />
 +
 
 +
<ggb_applet width="893" height="559"  version="3.2" ggbBase64="UEsDBBQACAAIALOq6TwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1srVVLj9s4DD63v0LQqUXRxI8kToB4im17KTDtHrJbtL3JNpNoR5YMSZ5x5tcvKdlJOrsF5tCTJZLm4+NHavtuaBW7B+uk0SVPZwlnoGvTSH0oee/3b9f83c3L7QHMASor2N7YVviS57OMk7yXNy9fbN3RPDChgslXCQ8l3wvlgDPXWRCNOwL4n+SiH6SSwp7+rP6B2ruLIjr5pLseo3jbo6xum1vppus8BOyU9B/lvWzAMmXqkq+WmDqevoL1shaq5IskSrKSZ0+UKMpJezRWPhrtyfzifI8Sxpx8BEQkI9l2HgrdQl8r2UihqZiQBxox9iAbfyz5epOjS5CHI+a6XBbRW22MbXYn56Flww+whjLLZ4s8W603SZZvinzN2SlqshW2oMjWRbHMl6t1sVgghpgwZrJIZ3mW5ekiWWyW61WxQdVp1GXJbLVK02WRZItik6PPGBvud+A99tIxMYCbAD1Y2ZwRp8sn996oi6gzUvsPovO9DTzIR9HOnygaAmepyD/0QcEoy7BNR6jvKjPsInB5dP3XqQu/hHyqwwejjGWWWrJEg/FbxW+woUTPVkmwSYLF6IOcnvXpJgsW4VvFb7BSUsfUxsLTqeo0mcJIx0iAzom+EzZKVIBs4KzX0t9OF2TN3VhpGu2/9G2FY3PNm7PL9Le5pJxZg+T/honOECk6f4/nwMsnjNzegdWgIu80dr43vWP3xO/Y2+C1gVq2eI2KETFB3fwbM4zSBg4WpsLiUEY8gza55vYT8XY+JUE5OCym9rhdsGBPxdLwexw8OjXCk4QmS0ELOHY+0EX3LVhZn6ETnKJhiH4KNBszCJvHhCXyBO4LiKj+BaFw3XRHQe7SkTbihAvlusTg7bNpxsCjnVNh87QSl+bblLJhrRiIXXQUlTOq97CrEUJ9a2rhw3qN+Y3bIk2C7UDTu6LTibZNOO3lAJdp/P8ldSG4PyKTNDgXptBfz5vQ2OcAPq6fbtzvrgPyHs6TNeuw8jDrZ5ogt2JPqDsD7nFHb8SE7h7fiQE97l8Nr1nJ0Bmbs4G9YYKz+X/6ue914AC//P7sGn5Xh5Nndjh5Nr7XCM2vqR4ejPHFvPkXUEsHCPrTDT02AwAAYwcAAFBLAQIUABQACAAIALOq6Tz60w09NgMAAGMHAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAAcAMAAAAA" framePossible = "true" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" /><br />
 +
 
 +
Beobachte, wie sich der Graph von f ändert, wenn a verändert wird.<br /><br />
 +
 
 +
Was stellst du dabei fest?<br />
 +
Was bewirkt also dieser Parameter a?<br />
 +
<br />
 +
<br />
 +
2. Aufgabe<br />
 +
Nun ist die Funktion <math>f(x)=\frac{b}{x} </math>, <math>x \in R \setminus \{ 0\} </math>, <math>b\in[-10;10]</math> gegeben.<br />
 +
b ist durch den Schieberegler veränderlich.<br />
 +
<ggb_applet width="674" height="510"  version="3.2" ggbBase64="UEsDBBQACAAIAHO16zwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1srVVLc9s4DD43v4LD0+6hNiXbsTJjJdPHpTPZ7sG7nXZvlATbbChSQ1KJ3F9fgJRsb9rO5NCTSADC48MHcHM3tJo9gvPKmpJnM8EZmNo2yuxL3ofd64Lf3V5t9mD3UDnJdta1MpR8Mcs5yXt1e/Vq4w/2iUkdTT4peCr5TmoPnPnOgWz8ASD8Ty77QWkl3fHv6ivUwZ8VyckH0/UYJbgeZXXb3Cs/XecxYKdVeK8eVQOOaVuX/HqFqePpE7igaqlLvhRJkpc8f6ZE0YK0B+vUN2sCmZ+d71DCmFffABHJSbaZx0I30NdaNUoaKibmgUaMPakmHDCF9RJdgtofMNeVKJK32lrXbI8+QMuG/8BZjL3MZwtRLIoiy0WeFWLN2TGp8tVytlqLdXG9vrlZ5esCMcSEMZM8m+ViWRTiJiuu82W+xGDHX+tibHjcQgjYS8/kAH4CdO9Uc0KcLh/8W6vPos4qE97JLvQu8mAxirbhSNEQOEdFvjF7DaMsxzYdoH6o7LBNwC2S63+OXfwl5lPt31ltHXNU6AoNxm+VvtGGEj1ZiWgjosXog5ye9NlNHi3it0rfaKWVSamNhWdT1ZmYwijPSIDOib4TNlpWgGzgrDcq3E8XZM3DWGmW7D/2bYVjc8mbk8vst7mknFmD5P+Mic4QKTp/SefIy2eM3DyAM6AT7wx2vre9Z4/E79Tb6LWBWrV4TYoRMUnd/BczTNIG9g6mwtJQJjyjVlxy+5l4M5+SoBw8FlMH3C5YcKBiafgDDh6dGhlIQpOloQUcuxDpYvoWnKpP0FWcomGIfgxEi2p+2jw2LpFncJ9BRPUvCIXrpjtIgjMbaSOPuFAuS4ze/rLNFHgMq+PmaRUuzdeZoLXZyoHYRUdZeav7ANsaITT3tpYhrteU37gtMhFt6adF3LvHkq8XdNipAc7D+PMddeZ3OCCRDHgfhzBcjps02OaIPW6fLpWJKxnIeww5WbMOC4+jfmIJUiu1hJoz4Br39ERM4O7wmRjQ4+6P4U9WsorN2cDZ/IdG7noTm8/PP744+9/VWvHC1ooXI3uJzfyS4/GlGJ/K2+9QSwcIn29+NiYDAABcBwAAUEsBAhQAFAAIAAgAc7XrPJ9vfjYmAwAAXAcAAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAABgAwAAAAA=" framePossible = "true" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" /><br />
 +
Achte auch dieses Mal darauf, was mit dem Funktionsgraphen von f passiert, wenn b verändert wird.<br /><br />
 +
 
 +
Was fällt dir dabei auf?<br />
 +
Was passiert in dem Fall b = 0 ?<br />
 +
Was geschieht mit dem Graphen, wenn b im negativen Bereich ist?<br /><br /><br />
 +
 
 +
3. Aufgabe<br />
 +
In dieser Aufgabe ist der veränderliche Parameter, diesmal c, erneut an einer anderen Stelle:<br />
 +
<math>f(x)=\frac{1}{x-c} </math>, <math>x \in R \setminus \{ c\} </math>, <math>c\in[-10;10]</math> gegeben.<br />
 +
 
 +
<ggb_applet width="674" height="510"  version="3.2" ggbBase64="UEsDBBQACAAIABaz6zwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1srVVNc9MwED3TX6HRiR6a2E7SuDNxGSgXZgocAh3gJtubRFSWPJLcOv317Ep2EgrM9MDJ0u56P96+Xa3e9I1iD2CdNLrg6SThDHRlaqm3Be/85iLnb67PVlswWyitYBtjG+ELPptknOSdvD57tXI788iECiZ3Eh4LvhHKAWeutSBqtwPwv8lF10slhd1/Ln9C5d1REZ180G2HUbztUFY19a1043UaArZK+vfyQdZgmTJVwS8XmDqe7sB6WQlV8HkSJVnBs2dKFM1IuzNWPhntyfzofIMSxpx8AkQkI9lqGgpdQVcpWUuhqZiQBxox9ihrv8MUlnN0CXK7w1wXSR69VcbYer13HhrW/wBrMPY8m8ySfJbnaZZkaZ4sOdtHVbbIJ4tlsswvl1dXi2yZI4aYMGaSpZMsmed5cpXml9k8m2Ow/b91ITY8rMF77KVjogc3Arq1sj4gTpcP7p1RR1FrpPY3ovWdDTyYDaK131M0BM5SkW/1VsEgy7BNO6juS9OvI3Cz6PrLvg2/hHzK7Y1RxjJLhS7QYPiW8RtsKNGDVRJskmAx+CCnB316lQWL8C3jN1gpqWNqQ+HpWHWajGGkYyRA50TfERslSkA2cNZp6W/HC7Lmfqg0jfafuqbEsTnlzcFl+t9cUs6sRvJ/w0QniBSdv8dz4OUzRq7uwWpQkXcaO9+ZzrEH4nfsbfBaQyUbvEbFgJigbn7FDKO0hq2FsbA4lBHPoE1Ouf1MvJqOSVAODoupPG4XLNhTsTT8HgePTrXwJKHJUtAAjp0PdNFdA1ZWB+gqTtEwRDcGmgwZhM1jwhJ5BvcRRFT/g1C4btqdIHfpQBuxx4VyWmLw9tHUQ+DBzqmweRqJS/MipWxYI3piFx1F6YzqPKwrhFDfmkr4sF5jfsO2SJNgSz/NZ3TaF3w5p8NG9nAcxr/vqCO//Q6JpMG5MIT+dNyExjYH7HH7tMN6dy1A5Ohoy1osOwz6gSNIrNgQak2PS9zRAzFCu8FHokd/m9f9OSsYumVT9rpnF6w652z6Rzs3nQ4U4EcHL67hfzU4eWGDkxfje4rR9JTp4b0YHszrX1BLBwjvQFbyKAMAAGIHAABQSwECFAAUAAgACAAWs+s870BW8igDAABiBwAADAAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAABAAEAOgAAAGIDAAAAAA==" framePossible = "true" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" /><br />
 +
Was ist nun festzustellen, wenn c verändert wird?<br />
 +
Für was ist also c verantwortlich?<br /><br />
 +
 
 +
4. Aufgabe<br />
 +
Nun sind die Aufgaben 1-3 miteinander verbunden, gegeben ist also die Funktion <math>f(x)=\frac{b}{x-c}+a </math>, <math>x \in R \setminus \{ c\} </math>, <math>a,b,c\in[-10;10]</math>.<br />
 +
<ggb_applet width="674" height="510"  version="3.2" ggbBase64="UEsDBBQACAAIAE216zwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vbfj9M4EH4+/gorT6DTtonTblOpXXQHL0jL8VAOHbw5ybQ169iR7eym/PU3YydtrwdiheABnuLMTObX983Eq+d9o9g9WCeNXifZJE0Y6MrUUu/WSee3V0Xy/ObJagdmB6UVbGtsI/w6ySc8IXknb578tnJ788CECibvJDysk61QDhLmWguidnsA/x+56HqppLCHN+VHqLw7KaKTV7rtMIq3Hcqqpr6VbnydhoCtkv6lvJc1WKZMtU6u55g6nt6B9bISap3M0ijh64RfKFGUk3ZvrPxktCfzk/MtShhz8hNgRzjJVtNQ6Aq6SslaCk3FhDzQiLEHWfs9prCYoUuQuz3mOk+L6K0yxtabg/PQsP4DWIOxZ3ySp0VeFBlPeVaki4QdoorPZ5P5Il0U14vlcs4XBfYQE8ZMeDbh6awo0mVWXPMZn2Gww5d1ITbcb8B7xNIx0YMbG7qzsj52nF5euT+NOolaI7V/IVrf2cCDfBBt/IGiYeMsFfmH3ikYZBxh2kN1V5p+ExuXR9dvD234JORT7l4YZSyzVOgcDYZnGZ/BhhI9WqXBJg0Wgw9yetRnSx4swrOMz2ClpI6pDYVnY9VZOoaRjpEAnRN9x94oUQKyIWGdlv52fEHW3A2VZtH+r64pcWzOeXN0mX03l5Qzq5H8/2CiE+wUnd/Hc+DlBSNXd2A1qMg7jch3pnPsnvgdsQ1ea6hkg69RMXRMEJp/Y4ZRWsPOwlhYHMrYz6BNz7l9IV5NxyQoB4fFVB63CxbsqVgafo+DR6daeJLQZCloAMfOB7rorgErq2PrqoSiYYhuDDQZMgibx4QlctHuUxNR/QVC4bpp94LcZQNtxAEXynmJwdtrUw+BBzunwuZpJC7Nq4yyYY3oiV10FKUzqvOwqbCF+tZUwof1GvMbtkWWBlv6KOd0OuApfr+VPZym8fNL6kRwv0cmaXAuTKE/nzehEefQfFw/7bDfXQvkPZxHa9Zi5WHWjzRBbkVMvoqO+LXR4csBnbz4CcEpL8HJfilw8mwAZ5H/UHCozG8Cp8cbkKPb1djcLd6wevS4fdo/Y2tWsil72rMrVj1jvzORsOn/IN12OmzQ5OTi0XV8L5DTR4KcPrrH512anv8ownVruG/e/AtQSwcIxS4MhlMDAAChCgAAUEsBAhQAFAAIAAgATbXrPMUuDIZTAwAAoQoAAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAACNAwAAAAA=" framePossible = "true" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" /><br />
 +
Beobachte den Graph von f für verschiedene Werte für a, b und c.<br /><br />
 +
Passen die Ergebnisse zu den Feststellungen aus den Aufgaben vorher?<br />
 +
Halte nun noch ein Mal abschließend fest, für was die Parameter verantwortlich sind!

Aktuelle Version vom 11. März 2012, 14:31 Uhr

1. Aufgabe

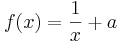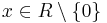Gegeben ist die Funktion f(x)=\frac{1}{x} + a, x \in R \setminus \{ 0\} , a\in[-10;10].
a ist dabei der Parameter, der durch den Schieberegler verändert werden kann.
Den Schieberegler kannst du bedienen, indem du einfach mit gedrückter Maustaste auf dem Punkt die Maus nach links bzw. rechts ziehst.


Beobachte, wie sich der Graph von f ändert, wenn a verändert wird.

Was stellst du dabei fest?
Was bewirkt also dieser Parameter a?


2. Aufgabe
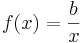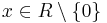Nun ist die Funktion f(x)=\frac{b}{x} , x \in R \setminus \{ 0\} , b\in[-10;10] gegeben.
b ist durch den Schieberegler veränderlich.


Achte auch dieses Mal darauf, was mit dem Funktionsgraphen von f passiert, wenn b verändert wird.

Was fällt dir dabei auf?
Was passiert in dem Fall b = 0 ?
Was geschieht mit dem Graphen, wenn b im negativen Bereich ist?


3. Aufgabe
In dieser Aufgabe ist der veränderliche Parameter, diesmal c, erneut an einer anderen Stelle:
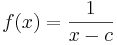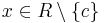f(x)=\frac{1}{x-c} , x \in R \setminus \{ c\} , c\in[-10;10] gegeben.


Was ist nun festzustellen, wenn c verändert wird?
Für was ist also c verantwortlich?

4. Aufgabe
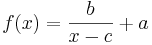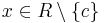Nun sind die Aufgaben 1-3 miteinander verbunden, gegeben ist also die Funktion f(x)=\frac{b}{x-c}+a , x \in R \setminus \{ c\} , a,b,c\in[-10;10].


Beobachte den Graph von f für verschiedene Werte für a, b und c.

Passen die Ergebnisse zu den Feststellungen aus den Aufgaben vorher?
Halte nun noch ein Mal abschließend fest, für was die Parameter verantwortlich sind!

Von „http://dmuw.zum.de/index.php?title=Mathematisches_Praktikum_SS2010/Simon_Möckl&oldid=31091“