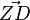Aufgaben 7. Klasse/Drehung/Seite 2: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
(overrightarrow durch vec ersetzt)
 
(41 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 1: Zeile 1:
 
=='''''<span style="color:#551A8B">Teilaufgabe b)</span>'''''==
 
=='''''<span style="color:#551A8B">Teilaufgabe b)</span>'''''==
  
−
'''Gib nun die Koordinaten von D an und berechne den Vektor <span style="text-decoration: overline;">ZD</span>'''
+
{| {{Prettytable}}
−
 
+
|- style="background-color:#EEA2AD"
−
<ggb_applet height="550" width="600" showResetIcon="true" filename="Drehung_b.ggb" />
+
! Flugdrache  !! Aufgabe
 +
|-
 +
|<ggb_applet height="550" width="550" showResetIcon="true" filename="Drehung_b.ggb" />||
  
  
 
<br />
 
<br />
 
<br />
 
<br />
−
'''Weißt du nicht mehr wie man Vektoren ausrechnet, schau dir den <span style="color:#551A8B">Tipp</span> an und das Kästchen "Vektorenberechnung" im Applet!''' {{Versteckt|
+
 
−
[[Vektoren berechnet man mit der Merkregel:"Spitze minus Fuß"!]]}}
+
'''1.) Gib nun die Koordinaten von D an und berechne den Vektor <math>\vec{ZD}</math>'''
 +
<br />
 +
Weißt du nicht mehr wie man Vektoren ausrechnet, schau dir den Tipp <span style="color:#551A8B">"Vektorenberechnung"</span> im Applet an und lass dir folgende <span style="color:#CD2626">Merkregel</span> geben!
 +
 
 +
<popup name="Merkregel">
 +
Vektoren berechnet man mit der <span style="color:#CD2626">Merkregel</span>: '''Spitze minus Fuß'''!
 +
</popup>
 +
 
 +
<u>Hinweis:</u> Mit dem Begriff '''Applet''' ist das Bild mit der Zeichnung gemeint!
  
 
<div class="lueckentext-quiz">
 
<div class="lueckentext-quiz">
Zeile 15: Zeile 25:
 
D = ('''-3(x- Koordinate)'''/'''4(y- Koordinate)''')
 
D = ('''-3(x- Koordinate)'''/'''4(y- Koordinate)''')
  
−
<span style="text-decoration: overline;">ZD</span> = ('''-4(x- Koordinate)'''/'''-1(y- Koordinate)''')
+
{|
 +
|-
 +
| <math>\vec{ZD}</math> = [[Bild:klammerMM.gif]] ||
 +
{|
 +
|-
 +
| '''-4 (x- Koordinate des Vektors)'''
 +
|-
 +
| '''-1 (y- Koordinate des Vektors)'''
 +
|}
 +
|| [[Bild:klammer2MM.gif]]
 +
|}
  
 
</div>
 
</div>
 +
<br />
  
−
'''Um wie viel Grad muss der Flugdrache um α gedreht werden werden, damit D‘ die Koordinaten (0/1) besitzt? Ziehe dafür am Schieberegler ω! Die Koordinaten von D' werden dir angezeigt! Probiers aus!'''
+
<br />
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
<br />
 +
<br />
 +
'''2.) Um wie viel Grad muss der Flugdrache um α gedreht werden, damit D‘ die Koordinaten <big>(0/1)</big> besitzt? Ziehe dafür am Schieberegler ω! Die Koordinaten von D' werden dir angezeigt! Probier's aus!'''
  
 
<div class="lueckentext-quiz">
 
<div class="lueckentext-quiz">
Zeile 26: Zeile 56:
  
 
</div>
 
</div>
 +
|}
  
−
'''Das war gar nicht so schwer oder! Üben wir das nochmal! Der Drachen wird nun um 47° gedreht, gib die Koordinaten von D‘ an und berechne den Vektor <span style="text-decoration: overline;">ZD'</span>'''
+
'''3.) Das war gar nicht so schwer oder! Üben wir das nochmal! Der Drachen wird nun um 47° gedreht, gib die Koordinaten von D‘ an und berechne den Vektor <math>\vec{ZD'}</math>!'''
 +
 
 +
Gehe bei deiner Berechnung so vor, wie in der 1. Aufgabe!
  
 
<div class="lueckentext-quiz">
 
<div class="lueckentext-quiz">
Zeile 33: Zeile 66:
 
D' = ('''-1(x- Koordinate)'''/'''1,4(y- Koordinate)''')
 
D' = ('''-1(x- Koordinate)'''/'''1,4(y- Koordinate)''')
  
−
<span style="text-decoration: overline;">ZD'</span> = ('''-2(x- Koordinate)'''/'''-3,6(y- Koordinate)''')
+
{|
 +
|-
 +
| <math>\vec{ZD'}</math> = [[Bild:klammerMM.gif]] ||
 +
{|
 +
|-
 +
| '''-2 (x- Koordinate des Vektors)'''
 +
|-
 +
| '''-3,6 (y- Koordinate des Vektors)'''
 +
|}
 +
|| [[Bild:klammer2MM.gif]]
 +
|}
  
 
</div>
 
</div>
  
−
'''Jetzt wird es ein bisschen schwerer, da du die Drehung nicht mit dem Schieberegler einstellen kannst. Aber das schaffst du! Gib nun die Koordinaten von D‘ an, wenn der Drache um 180° gedreht wurde und berechne den Vektor ZD‘'''
+
'''4.) Jetzt wird es ein bisschen schwerer, da du die Drehung nicht mehr mit dem Schieberegler einstellen kannst. Aber das schaffst du! Gib nun die Koordinaten von D‘ an, wenn der Drache um 180° gedreht wurde und berechne den Vektor <math>\vec{ZD'}</math>!'''
 +
 
 +
<u>Hinweis</u>: Überlege dir, wo D' ungefähr liegen müsste und wende das Steigungsdreieck, welches dir im Tipp <span style="color:#551A8B">"Vektorenberechnung"</span> angezeigt wird, an!!
  
 
<div class="lueckentext-quiz">
 
<div class="lueckentext-quiz">
Zeile 43: Zeile 88:
 
D' = ('''5(x- Koordinate)'''/'''6(y- Koordinate)''')
 
D' = ('''5(x- Koordinate)'''/'''6(y- Koordinate)''')
  
−
<span style="text-decoration: overline;">ZD'</span> = ('''4(x- Koordinate)'''/'''1(y- Koordinate)''')
+
{|
 +
|-
 +
| <math>\vec{ZD'}</math> = [[Bild:klammerMM.gif]] ||
 +
{|
 +
|-
 +
| '''4 (x- Koordinate des Vektors)'''
 +
|-
 +
| '''1 (y- Koordinate des Vektors)'''
 +
|}
 +
|| [[Bild:klammer2MM.gif]]
 +
|}
  
 
</div>
 
</div>
  
−
'''→[[Aufgaben 7. Klasse/Drehung/Seite 3|Na, neugierig auf Teilaufgabe c)?]]'''
+
'''→[[Aufgaben 7. Klasse/Drehung/Seite 3|Super gemacht! Auf zu Teilaufgabe c)?]]'''

Aktuelle Version vom 20. März 2012, 19:21 Uhr

Teilaufgabe b)

Flugdrache Aufgabe




1.) Gib nun die Koordinaten von D an und berechne den Vektor \vec{ZD}
Weißt du nicht mehr wie man Vektoren ausrechnet, schau dir den Tipp "Vektorenberechnung" im Applet an und lass dir folgende Merkregel geben!

Hinweis: Mit dem Begriff Applet ist das Bild mit der Zeichnung gemeint!

D = (-3(x- Koordinate)/4(y- Koordinate))

\vec{ZD} = KlammerMM.gif
-4 (x- Koordinate des Vektors)
-1 (y- Koordinate des Vektors)
Klammer2MM.gif








2.) Um wie viel Grad muss der Flugdrache um α gedreht werden, damit D‘ die Koordinaten (0/1) besitzt? Ziehe dafür am Schieberegler ω! Die Koordinaten von D' werden dir angezeigt! Probier's aus!

α = 62(°)

3.) Das war gar nicht so schwer oder! Üben wir das nochmal! Der Drachen wird nun um 47° gedreht, gib die Koordinaten von D‘ an und berechne den Vektor 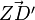\vec{ZD'}!

Gehe bei deiner Berechnung so vor, wie in der 1. Aufgabe!

D' = (-1(x- Koordinate)/1,4(y- Koordinate))

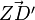\vec{ZD'} = KlammerMM.gif
-2 (x- Koordinate des Vektors)
-3,6 (y- Koordinate des Vektors)
Klammer2MM.gif

4.) Jetzt wird es ein bisschen schwerer, da du die Drehung nicht mehr mit dem Schieberegler einstellen kannst. Aber das schaffst du! Gib nun die Koordinaten von D‘ an, wenn der Drache um 180° gedreht wurde und berechne den Vektor 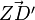\vec{ZD'}!

Hinweis: Überlege dir, wo D' ungefähr liegen müsste und wende das Steigungsdreieck, welches dir im Tipp "Vektorenberechnung" angezeigt wird, an!!

D' = (5(x- Koordinate)/6(y- Koordinate))

\vec{ZD'} = KlammerMM.gif
4 (x- Koordinate des Vektors)
1 (y- Koordinate des Vektors)
Klammer2MM.gif

→Super gemacht! Auf zu Teilaufgabe c)?

Von „http://dmuw.zum.de/index.php?title=Aufgaben_7._Klasse/Drehung/Seite_2&oldid=31104“