4.Station: Unterschied zwischen den Versionen
K |
K |
||
| (24 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | <div style="margin:0; margin-right:4px; margin-left:0px; border:2px solid #f4f0e4; padding: 0em 0em 0em 1em; background-color:#f4f0e4;"> | ||
| + | [[Lernpfade/Zentrische Streckung/Eigenschaften der zentrischen Streckung|1. Station: Fixelemente]] - [[Lernpfade/Zentrische Streckung/Eigenschaften der zentrischen Streckung/2.Station|2. Station: Geradentreue und Parallelentreue]] - [[Lernpfade/Zentrische Streckung/Eigenschaften der zentrischen Streckung/3.Station|3. Station: Winkeltreue, Längentreue und Flächeninhaltstreue]] - [[Lernpfade/Zentrische Streckung/Eigenschaften der zentrischen Streckung/4.Station|4. Station: Längenverhältnistreue]] - [[Lernpfade/Zentrische Streckung/Eigenschaften der zentrischen Streckung/5.Station|5. Station: Kreistreue]] - [[Lernpfade/Zentrische Streckung/Eigenschaften der zentrischen Streckung/6.Station|6. Station: Zusammenfassung]] - [[Lernpfade/Zentrische Streckung/Eigenschaften der zentrischen Streckung/7.Station|7. Station: Übung]] | ||
| + | </div> | ||
| + | <br> | ||
| + | |||
==4. Station: Längenverhältnistreue== | ==4. Station: Längenverhältnistreue== | ||
| + | [[Bild:Porzelt_lobenderDia3.jpg]] | ||
<div style="border: 2px solid #ffd700; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid #ffd700; background-color:#ffffff; padding:7px;"> | ||
| − | :'''Längenverhältnistreue''' liegt vor, wenn das Längenverhältnis der Bildstrecke gleich dem der Urstrecke ist. | + | [[Bild:Porzelt_Panto-2.jpg|left]] <br>'''Längenverhältnistreue''' liegt vor, wenn das Längenverhältnis der Bildstrecke gleich dem der Urstrecke ist. |
| + | <br> | ||
</div> | </div> | ||
<br> | <br> | ||
| + | <div style="border: 2px solid #00CD00; background-color:#ffffff; padding:7px;"> | ||
{| | {| | ||
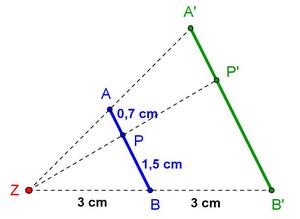
|[[Bild:Porzelt_Verhältnistreu.jpg]]|| '''Arbeitsauftrag:''' | |[[Bild:Porzelt_Verhältnistreu.jpg]]|| '''Arbeitsauftrag:''' | ||
1.Berechne den Streckungsfaktor k.<br> | 1.Berechne den Streckungsfaktor k.<br> | ||
| − | 2.Berechne <math>\overline{A'P'}</math> und <math>\overline{P'B'}</math>. | + | 2.Berechne <math>\overline{A'P'}</math> und <math>\overline{P'B'}</math>. (Tipp: Beim Eintragen Leerzeichen zwischen Zahl und Einheit nicht vergessen!) |
<br> | <br> | ||
<br> | <br> | ||
3.Berechne <math>{\overline{AP}\over\overline{PB}}</math> und <math>{\overline{A'P'}\over\overline{P'B'}}</math>. Runde auf 2 Nachkommastellen. | 3.Berechne <math>{\overline{AP}\over\overline{PB}}</math> und <math>{\overline{A'P'}\over\overline{P'B'}}</math>. Runde auf 2 Nachkommastellen. | ||
|} | |} | ||
| + | </div> | ||
<br> | <br> | ||
| − | + | '''''Mit Hilfe der folgenden Lückentexte kannst du den Arbeitsauftrag lösen.'''''<br> | |
| − | < | + | '''''Denk konzentriert nach und setze die richtige Aussage in die passende Lücke ein, um die Ergebnisse berechnen zu können:'''''<br> |
| − | + | <div style="border: 2px solid #00CD00; background-color:#ffffff; padding:7px;"> | |
| − | {''' | + | <div class="lueckentext-quiz"> |
| − | + | Lösung zu 1: <br> | |
| − | + | <math>\mid k \mid</math> = '''<math>\overline{ZB'}</math>''' : '''<math>\overline{ZB}</math>'''<br> | |
| − | + | Einsetzen der Werte:<br> | |
| − | + | <math>\mid k \mid</math> = '''6''' : '''3''' = '''2 (Berechne das Ergebnis mit dem Taschenrechner)'''<br> | |
| − | + | </div> | |
| − | + | {| | |
| − | + | |[[Bild:Porzelt_Verhältnistreu.jpg]]||<div class="lueckentext-quiz"> | |
| − | + | Lösung zu 2:<br> | |
| + | <math>\overline{A'P'}</math> = '''<math>\mid k \mid</math>''' <math>\cdot</math> '''<math>\overline{AP}</math>'''<br> | ||
| + | Einsetzen der Werte:<br> | ||
| + | <math>\overline{A'P'}</math> = '''2''' <math>\cdot</math> '''0,7 cm''' = '''1,4 cm (Berechne das Ergebnis mit dem Taschenrechner und gib die Einheit mit an!)'''<br> | ||
| + | <br> | ||
| + | <math>\overline{P'B'}</math> = '''<math>\mid k \mid</math>''' <math>\cdot</math> '''<math>\overline{PB}</math>'''<br> | ||
| + | Einsetzen der Werte:<br> | ||
| + | <math>\overline{P'B'}</math> = '''2''' <math>\cdot</math> '''1,5 cm''' = '''3 cm (Berechne das Ergebnis mit dem Taschenrechner und gib die Einheit mit an!)'''<br> | ||
| + | </div> | ||
| + | |} | ||
| − | + | <div class="lueckentext-quiz"> | |
| − | + | Lösung zu 3:<br> | |
| − | + | Einsetzen der Werte:<br> | |
| − | + | <math>{\overline{AP}\over\overline{PB}}</math> = '''<math>{0,7\ cm \over 1,5\ cm}</math>''' = '''0,47 (Berechne das Ergebnis mit dem Taschenrechner)'''<br> | |
| − | + | <math>{\overline{A'P'}\over\overline{P'B'}}</math> = '''<math>{1,4\ cm \over 3\ cm}</math>''' = '''0,47 (Berechne das Ergebnis mit dem Taschenrechner)'''<br> | |
| − | + | </div> | |
| − | + | | |
| − | + | </div> | |
| − | + | <br> | |
| − | + | [[Bild:Porzelt_lobenderPanto6.jpg]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | </ | + | |
<br> | <br> | ||
| − | :Warum ist <math>{\overline{AP}\over\overline{PB}}</math> = <math>{\overline{A'P'}\over\overline{P'B'}}</math>? | + | <div style="border: 2px solid #9c9c9c; background-color:#ffffff; padding:7px;"> |
| + | [[Bild:Porzelt_fragenderDia-1.jpg |left]] | ||
| + | <br> | ||
| + | Warum ist <math>{\overline{AP}\over\overline{PB}}</math> = <math>{\overline{A'P'}\over\overline{P'B'}}</math>?<br> | ||
| + | <br> | ||
| + | </div> | ||
| + | <br> | ||
| + | <div style="border: 2px solid #0000ff; background-color:#ffffff; padding:7px;"> | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
| − | Für <math>\overline{ | + | Für <math>\overline{A'P'}</math> kann man auch '''<math>\mid k\mid \cdot \overline{AP}</math>''' und für <math>\overline{P'B'}</math> kann man '''<math>\mid k\mid \cdot \overline{PB}</math>''' einsetzen. <br> |
| − | Daraus folgt: <math>{\overline{ | + | Daraus folgt: <math>{\overline{A'P'}\over\overline{P'B'}} ={{|k|}\over{|k|}}\cdot</math> '''<math>{\overline{AP}\over\overline{PB}}</math>'''.<br> |
| − | + | <math>\mid k\mid</math> kann man rauskürzen, so dass '''<math>{\overline{A'P'}\over\overline{P'B'}}</math>''' <math>= {\overline{AP}\over\overline{PB}}</math> gilt. | |
</div> | </div> | ||
| + | | ||
| + | </div> | ||
| + | |||
| + | <br> | ||
| + | [[Bild:Porzelt_lobenderDia5.jpg]] | ||
<br> | <br> | ||
| Zeile 57: | Zeile 81: | ||
</div> | </div> | ||
<br> | <br> | ||
| − | <div align=" | + | <br> |
| − | <div align="left">[[ | + | <div align="left">[[Lernpfade/Zentrische Streckung/Eigenschaften der zentrischen Streckung/5.Station|<math>\Rightarrow</math> Weiter zur 5. Station: Kreistreue]]</div> |
| + | <br> | ||
| + | <div align="left">[[Lernpfade/Zentrische Streckung/Eigenschaften der zentrischen Streckung/3.Station|<math>\Leftarrow</math> Zurück zur 3. Station: Winkeltreue, Längentreue und Flächeninhaltstreue]]</div> | ||
Aktuelle Version vom 8. September 2009, 17:43 Uhr
1. Station: Fixelemente - 2. Station: Geradentreue und Parallelentreue - 3. Station: Winkeltreue, Längentreue und Flächeninhaltstreue - 4. Station: Längenverhältnistreue - 5. Station: Kreistreue - 6. Station: Zusammenfassung - 7. Station: Übung
4. Station: Längenverhältnistreue
Längenverhältnistreue liegt vor, wenn das Längenverhältnis der Bildstrecke gleich dem der Urstrecke ist.
 |
Arbeitsauftrag:
1.Berechne den Streckungsfaktor k. |
Mit Hilfe der folgenden Lückentexte kannst du den Arbeitsauftrag lösen.
Denk konzentriert nach und setze die richtige Aussage in die passende Lücke ein, um die Ergebnisse berechnen zu können:
Lösung zu 1:
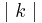 =
= 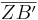 :
: 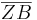
Einsetzen der Werte:
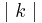 = 6 : 3 = 2 (Berechne das Ergebnis mit dem Taschenrechner)
= 6 : 3 = 2 (Berechne das Ergebnis mit dem Taschenrechner)
Lösung zu 3:
Einsetzen der Werte:
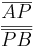 =
= 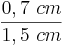 = 0,47 (Berechne das Ergebnis mit dem Taschenrechner)
= 0,47 (Berechne das Ergebnis mit dem Taschenrechner)
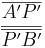 =
= 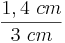 = 0,47 (Berechne das Ergebnis mit dem Taschenrechner)
= 0,47 (Berechne das Ergebnis mit dem Taschenrechner)
Für 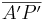 kann man auch
kann man auch 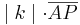 und für
und für 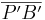 kann man
kann man 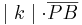 einsetzen.
einsetzen.
Daraus folgt: 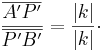
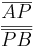 .
.
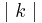 kann man rauskürzen, so dass
kann man rauskürzen, so dass 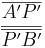
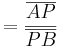 gilt.
gilt.
Ist die zentrische Streckung längenverhältnistreu? (Ja) (!Nein)



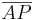
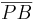



 Weiter zur 5. Station: Kreistreue
Weiter zur 5. Station: Kreistreue Zurück zur 3. Station: Winkeltreue, Längentreue und Flächeninhaltstreue
Zurück zur 3. Station: Winkeltreue, Längentreue und Flächeninhaltstreue
