Lineare Gleichungssysteme grafisch lösen: Unterschied zwischen den Versionen
| Zeile 36: | Zeile 36: | ||
{{Merke|'''Wichtige Begriffe''' <br> | {{Merke|'''Wichtige Begriffe''' <br> | ||
| − | *Zwei lineare Gleichungen mit denselben beiden Varaiablen , die durch (und zugleich) miteinander verknüpt sind, bilden zusammen ein '''Lineares Gleichungssystem''' mit 2 Variablen. | + | * Zwei lineare Gleichungen mit denselben beiden Varaiablen , die durch "v" (und zugleich) miteinander verknüpt sind, bilden zusammen |
| + | ein '''Lineares Gleichungssystem''' mit 2 Variablen. | ||
* Ein Zahlenpaar, dass beide Gleichungen eines linearen Gleichungssystems löst, heißt '''Lösung des Linearen Gleichungssystems'''. | * Ein Zahlenpaar, dass beide Gleichungen eines linearen Gleichungssystems löst, heißt '''Lösung des Linearen Gleichungssystems'''. | ||
* Die Lösung ist der Schnittpunkt der beiden Geraden, die zu den Gleichungen gehören. | * Die Lösung ist der Schnittpunkt der beiden Geraden, die zu den Gleichungen gehören. | ||
Version vom 23. November 2009, 20:12 Uhr
Station 1
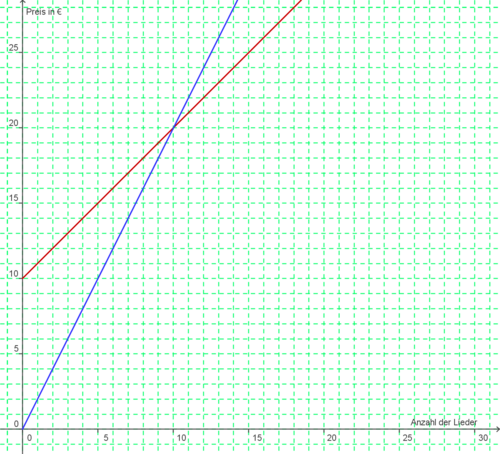
Tom und Susi möchten sich aus dem Internet Musik herunterladen. Tom hat einen Anbieter gefunden, bei dem er eine Grundgebühr von 10 € zahlen muss und dann jedes Lied 1 € kostet. Susi dagegen hat einen Anbieter gefunden, bei dem Sie keine Grundgebühr zahlt und dafür jedes Lied 2 € kostet.
Im Koordinatensystem sind die beiden Verträge von Susi und Tom dargestellt. Versuche nun folgende Fragen dazu zu beantworten!
Welche Farbe hat die Halbgerade, die zum Anbieter von Tom gehört? (!blau) (rot)
Welche Farbe hat die Halbgerade, die zum Anbieter von Susi gehört? (blau) (!rot)
Wie lautet die Gleichung der roten Halbgeraden? (!y= 2x+10) (y= x+10) (!y= 10x)
Wie lautet die Gleichung der blauen Halbgeraden? (!y= 2x+1) (!y= 3x) (y= 2x)
Wie viele Lieder muss man herunterladen, damit beide Anbieter gleich teuer sind? (10) (!15) (!20)
Wie viel muss man für diese Anzahl der Lieder bezahlen? (!10 €) (!15 €) (20 €)
Wie nennt man den Punkt, in dem sich die beiden Geraden schneiden? (Schnittpunkt) (!Fixpunkt) (!Treffpunkt)
Wenn du weniger als 80% richtig hast, dann mache die Übung nochmal!
30px Merke
Wichtige Begriffe
ein Lineares Gleichungssystem mit 2 Variablen.
|
Somit lautet also die Lösung für das obige Lineare Gleichungssystem L={(10/20)}