Lineare Gleichungssysteme grafisch lösen/Station 2: Unterschied zwischen den Versionen
| Zeile 1: | Zeile 1: | ||
=Station 2= | =Station 2= | ||
| + | |||
| + | [[Bild:Motivation_Hatos_3.bmp|600px]] | ||
<div style="border: 2px solid #0000ee; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid #0000ee; background-color:#ffffff; padding:7px;"> | ||
| − | Wie du siehst kann man ein Lineares Gleichungssystem grafisch lösen. Du musst also nur die beiden Geraden, die zu den beiden Gleichungen gehören in ein Koordinatensystem einzeichnen und den Schnittpunkt ablesen. | + | '''''Wie du siehst kann man ein Lineares Gleichungssystem grafisch lösen. Du musst also nur die beiden Geraden, die zu den beiden Gleichungen gehören in ein Koordinatensystem einzeichnen und den Schnittpunkt ablesen.''''' |
| − | Versuche nun das folgende Lineare Gleichungssystem zu lösen: | + | '''''Versuche nun das folgende Lineare Gleichungssystem zu lösen:''''' |
| Zeile 11: | Zeile 13: | ||
| − | 1. Schritt: Zuerst musst du die beiden Gleichungen nach y auflösen, damit du Sie einzeichnen kannst! | + | '''1. Schritt: Zuerst musst du die beiden Gleichungen nach y auflösen, damit du Sie einzeichnen kannst!''' |
<div class="multiplechoice-quiz"> | <div class="multiplechoice-quiz"> | ||
| Zeile 21: | Zeile 23: | ||
</div> | </div> | ||
| − | 2. Schritt: Nun kann man die Geraden in ein Koordinatensystem einzeichnen. | + | '''2. Schritt: Nun kann man die Geraden in ein Koordinatensystem einzeichnen.''' |
{| | {| | ||
| Zeile 39: | Zeile 41: | ||
|} | |} | ||
| − | + | '''3. Schritt: Du kannst die Probe machen, indem du die Koordinaten des Schnittpunktes in deine beiden Anfangsgleichungen einsetzt!''' | |
| − | + | <div class="lueckentext-quiz"> | |
Gleichung 1: y + 3 = 2x | Gleichung 1: y + 3 = 2x | ||
| Zeile 61: | Zeile 63: | ||
</div> | </div> | ||
| − | + | [[Bild:Motivation_Hatos_4.bmp|600px]] | |
Version vom 24. November 2009, 22:44 Uhr
Station 2
Wie du siehst kann man ein Lineares Gleichungssystem grafisch lösen. Du musst also nur die beiden Geraden, die zu den beiden Gleichungen gehören in ein Koordinatensystem einzeichnen und den Schnittpunkt ablesen.
Versuche nun das folgende Lineare Gleichungssystem zu lösen:
(I) y + 3 = 2x und (II) y + x = 3
1. Schritt: Zuerst musst du die beiden Gleichungen nach y auflösen, damit du Sie einzeichnen kannst!
Wie lautet die Gleichung (I) nach y aufgelöst? (!y= 2x+3) (y= 2x-3) (!y= 1/2x)
Wie lautet die Gleichung (II) nach y aufgelöst? (y= -x+3) (!y= x+3) (!y= -x-3)
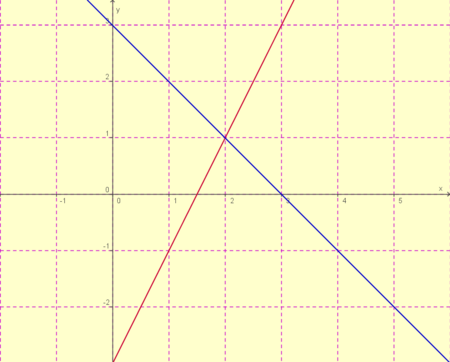
2. Schritt: Nun kann man die Geraden in ein Koordinatensystem einzeichnen.
|
Die rote Gerade gehört zu folgender Gleichung: (!y = - x + 3) (y = 2x - 3) Die blaue Gerade gehört zu folgender Gleichung: (y = - x + 3) (!y = 2x - 3) Wie lautet der Schnittpunkt der beiden Geraden? (!1/2) (2/1) (!3/0) |
3. Schritt: Du kannst die Probe machen, indem du die Koordinaten des Schnittpunktes in deine beiden Anfangsgleichungen einsetzt!
Gleichung 1: y + 3 = 2x
1 + 3 = 4
4 = 4
Disese Aussage ist wahr
Gleichung 2: y + x = 3
1 + 2 = 3
3 = 3
Diese Aussage ist wahr
Also lautet die Lösung dieses Linearen Gleichungssystmes
L = {(2/1)}
