Aufgaben 7. Klasse/Satz des Thales/Seite 3: Unterschied zwischen den Versionen
Aus DMUW-Wiki
| (8 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
== '''''<span style="color:#551A8B">Teilaufgabe c)</span>''''' == | == '''''<span style="color:#551A8B">Teilaufgabe c)</span>''''' == | ||
| − | '''Das machst du bis jetzt sehr gut! | + | ===='''<span style="color:#551A8B">Das machst du bis jetzt sehr gut!</span> Du siehst nun im Applet weitere Konstruktionen an diesem Thaleskreis, mit denen du arbeiten sollst.'''==== |
| − | + | ||
| − | + | ||
{| {{Prettytable}} | {| {{Prettytable}} | ||
| − | |- style="background-color:# | + | |- style="background-color:#CDB38B" |
! Riesenrad !! Aufgabe | ! Riesenrad !! Aufgabe | ||
|- | |- | ||
| Zeile 14: | Zeile 12: | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| − | '''Überprüfe, welche Aussagen wahr sind! Du kannst dazu wieder <span style="color:#00CD00">Carla</span> im Applet bewegen! Füge am Ende die Buchstaben der richtigen Antworten zu einem Lösungswort zusammen!''' | + | '''Überprüfe, welche folgenden Aussagen wahr sind! Du kannst dazu wieder <span style="color:#00CD00">Carla</span> im Applet bewegen! Füge am Ende die Buchstaben der richtigen Antworten zu einem Lösungswort zusammen!''' |
<quiz display="simple"> | <quiz display="simple"> | ||
| − | {Das Maß des Winkels | + | {Das Maß des Winkels '''γ''' berechnet sich aus den Winkeln '''δ''' und '''ε'''} |
+ Richtig (T) | + Richtig (T) | ||
- Falsch (E) | - Falsch (E) | ||
| − | {Die Summe der Winkel | + | {Die Summe der Winkel '''α''' und '''β''' beträgt immer '''60°'''} |
- Richtig (L) | - Richtig (L) | ||
+ Falsch (H) | + Falsch (H) | ||
| − | {Die Strecke <span style="text-decoration: overline;">AC</span> ist immer so lang wie die Strecke <span style="text-decoration: overline;">BC</span>} | + | {Die Strecke '''<span style="text-decoration: overline;">AC</span>''' ist immer '''so lang''' wie die Strecke '''<span style="text-decoration: overline;">BC</span>'''} |
- Richtig (F) | - Richtig (F) | ||
+ Falsch (A) | + Falsch (A) | ||
| − | {Die Strecke <span style="text-decoration: overline;">AM</span> ist immer so lang wie die Strecke <span style="text-decoration: overline;">MC</span>} | + | {Die Strecke '''<span style="text-decoration: overline;">AM</span>''' ist immer '''so lang''' wie die Strecke '''<span style="text-decoration: overline;">MC</span>'''} |
+ Richtig (L) | + Richtig (L) | ||
- Falsch (D) | - Falsch (D) | ||
| − | {Die Strecke <span style="text-decoration: overline;">MB</span> ist immer so lang wie die Strecke <span style="text-decoration: overline;">MC</span>} | + | {Die Strecke '''<span style="text-decoration: overline;">MB</span>''' ist immer '''so lang''' wie die Strecke '''<span style="text-decoration: overline;">MC</span>'''} |
+ Richtig (E) | + Richtig (E) | ||
- Falsch (P) | - Falsch (P) | ||
| − | {Die Winkel | + | {Die Winkel '''α''' und '''β''' sind immer '''gleich groß'''} |
- Richtig (I) | - Richtig (I) | ||
+ Falsch (S) | + Falsch (S) | ||
| − | {Die Winkel | + | {Die Winkel '''ε''' und '''β''' sind immer '''gleich groß'''} |
+ Richtig (K) | + Richtig (K) | ||
- Falsch (R) | - Falsch (R) | ||
| − | {Die Winkel | + | {Die Winkel '''α''' und '''δ''' sind immer '''gleich groß'''} |
+ Richtig (R) | + Richtig (R) | ||
- Falsch (O) | - Falsch (O) | ||
| − | {Die beiden Winkel | + | {Die beiden Winkel '''α''' und '''β''' sind '''nie''' maßgleich} |
- Richtig (T) | - Richtig (T) | ||
+ Falsch (E) | + Falsch (E) | ||
| − | {Die Summer der Winkel | + | {Die Summer der Winkel '''δ''' und '''ε''' ist immer '''90°'''} |
+ Richtig (I) | + Richtig (I) | ||
- Falsch (U) | - Falsch (U) | ||
| − | {Die Winkel | + | {Die Winkel '''α''', '''β''', '''ε''' und '''δ''' ergeben zusammen immer '''360°'''} |
- Richtig (F) | - Richtig (F) | ||
+ Falsch (S) | + Falsch (S) | ||
| Zeile 76: | Zeile 74: | ||
[[Bild:Gleichschenklig_CM.png]]}} | [[Bild:Gleichschenklig_CM.png]]}} | ||
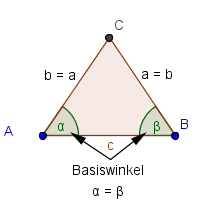
| − | Tipp: Betrachte die Eigenschaften dieses Dreiecks genauer! | + | <u>Tipp:</u> Betrachte die Eigenschaften dieses Dreiecks genauer! |
Aktuelle Version vom 19. Januar 2010, 17:56 Uhr
Teilaufgabe c)
Das machst du bis jetzt sehr gut! Du siehst nun im Applet weitere Konstruktionen an diesem Thaleskreis, mit denen du arbeiten sollst.
| Riesenrad | Aufgabe |
|---|---|
|
Schreibe das Wort nicht in Großbuchstaben, sondern ganz normal! Einen besonderen Halbkreis nennt man Thaleskreis(Lösungswort)! |
Schau dir nun als Wiederholung folgende Zeichnung an und überlege dir, welche Winkel im Applet Basiswinkel sind!
Tipp: Betrachte die Eigenschaften dieses Dreiecks genauer!