Geometrie: Trigonometrie: Unterschied zwischen den Versionen
Aus DMUW-Wiki
K |
K |
||
| (31 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | ''' | + | <div style="border: 4px solid #8B3A3A ; background-color:#EEC591; padding:7px;"> |
| − | + | <big><span style="color:#8B3A3A ">'''Trigonometrie</span>'''</big></div> | |
| + | <br /> | ||
| + | {| | ||
| + | |- | ||
| + | | width="450" | | ||
<div class="multiplechoice-quiz"> | <div class="multiplechoice-quiz"> | ||
| + | <div style="border: 4px solid #8B3A3A ; background-color:#EEC591; padding:7px;"> | ||
| + | '''Welche Werte stimmen? Wenn du die Antwort nicht aus dem Kopf weißt, kannst du das Maß mit Hilfe des GeoGebra Applets herausfinden, indem du den Punkt <span style="color: #CD2626 ">P</span> bewegst. Du darfst aber auch diesen Taschenrechner zu Hilfe nehmen: (am besten mit rechter Maustaste anklicken und in neuem Fenster öffnen) '''[http://web2.0calc.com/ Taschenrechner] <br />''Auch mehrere Antworten sind möglich.''</div> | ||
| − | '''cos 0° = '''(1) (!0) (!<math>\approx 0,53122</math>) | + | |
| + | '''cos 0° = '''(1) (!0) (!<math>\approx 0{,}53122</math>) | ||
'''sin 30° = '''(!<math>\approx 1</math>) (!0) (0,5) | '''sin 30° = '''(!<math>\approx 1</math>) (!0) (0,5) | ||
| Zeile 11: | Zeile 18: | ||
'''cos 60° = '''(0,5) (!0) (!1) | '''cos 60° = '''(0,5) (!0) (!1) | ||
| − | '''sin 45° = ''' (!0,5) (!1) (<math>\approx 0,70711</math>) | + | '''sin 45° = ''' (!0,5) (!1) (<math>\approx 0{,}70711</math>) |
| − | '''sin 90° = '''(1) (!0) (!<math>\approx 0,93962</math>) | + | '''sin 90° = '''(1) (!0) (!<math>\approx 0{,}93962</math>) |
| − | '''tan 30° = '''(!1) (!<math>\approx 0,83911</math>) (<math>\approx 0,57735</math>) | + | '''tan 30° = '''(!1) (!<math>\approx 0{,}83911</math>) (<math>\approx 0{,}57735</math>) |
'''tan 0° = '''(!0,5) (0) (!<math>\approx 1</math>) | '''tan 0° = '''(!0,5) (0) (!<math>\approx 1</math>) | ||
| − | '''cos 90° = '''(!<math>\approx 0,5</math>) (0) (!1) | + | '''cos 90° = '''(!<math>\approx 0{,}5</math>) (0) (!1) |
| + | |||
| + | </div> | ||
| + | || | ||
| + | :::<ggb_applet height="500" width="300" filename="Haas_Winkelmaßneu2.ggb" /> | ||
| + | |} | ||
| + | |||
| + | {| | ||
| + | |- | ||
| + | | width="400" | | ||
| + | <div class="multiplechoice-quiz"> | ||
| + | <div style="border: 4px solid #8B3A3A ; background-color:#EEC591; padding:7px;"> | ||
| + | '''Versuche nun, den/die jeweiligen Winkel herauszufinden. Benutze wieder das GeoGebra Applet, wenn du dir unsicher bist. Du darfst aber auch diesen Taschenrechner zu Hilfe nehmen: (am besten mit rechter Maustaste anklicken und in neuem Fenster öffnen) '''[http://web2.0calc.com/ Taschenrechner] <br />''Auch mehrere Antworten sind möglich.'' | ||
| + | </div> | ||
| + | |||
| + | |||
| + | '''<math>\sin (\alpha) \approx 0{,}86603 \Leftrightarrow \alpha = </math>''' | ||
| + | |||
| + | (120°) (!150°) (60°) | ||
| + | |||
| + | '''<math>\cos (\alpha) = - 0{,}5 \Leftrightarrow \alpha = </math>''' | ||
| + | |||
| + | (120°) (!90°) (240°) | ||
| + | |||
| + | '''<math>\tan (\alpha) \approx 0{,}83911 \Leftrightarrow \alpha = </math>''' | ||
| + | |||
| + | (!50°) (!70°) (40°) | ||
| + | |||
| + | '''<math>\sin (\alpha) = {1 \over 2} \sqrt{3} \Leftrightarrow \alpha = </math>''' | ||
| + | |||
| + | (!40°) (60°) (!240°) | ||
| + | |||
| + | '''<math>\cos (\alpha) = 0\Leftrightarrow \alpha = </math>''' | ||
| + | |||
| + | (!30°) (90°) (270°) | ||
| + | |||
| + | '''<math>\tan (\alpha) = 0 \Leftrightarrow \alpha = </math>''' | ||
| + | |||
| + | (180°) (!45°) (90°) | ||
| − | |||
</div> | </div> | ||
| + | || | ||
| + | <ggb_applet height="550" width="400" filename="Haas_Winkelmaß-groß3.ggb" /> | ||
| + | |} | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <div align="left">[[Aufgabentypen/Algebra: Potenzen und Potenzfunktionen|<math>\Leftarrow</math> Zurück zu 10. Klasse Algebra]]</div> | ||
Aktuelle Version vom 20. Juli 2009, 11:02 Uhr
Trigonometrie
|
Welche Werte stimmen? Wenn du die Antwort nicht aus dem Kopf weißt, kannst du das Maß mit Hilfe des GeoGebra Applets herausfinden, indem du den Punkt P bewegst. Du darfst aber auch diesen Taschenrechner zu Hilfe nehmen: (am besten mit rechter Maustaste anklicken und in neuem Fenster öffnen) Taschenrechner
Auch mehrere Antworten sind möglich.
sin 30° = (! tan 45° = (!2,5) (!0) (1) cos 60° = (0,5) (!0) (!1) sin 45° = (!0,5) (!1) ( sin 90° = (1) (!0) (! tan 30° = (!1) (! tan 0° = (!0,5) (0) (! cos 90° = (! |
|
|
Versuche nun, den/die jeweiligen Winkel herauszufinden. Benutze wieder das GeoGebra Applet, wenn du dir unsicher bist. Du darfst aber auch diesen Taschenrechner zu Hilfe nehmen: (am besten mit rechter Maustaste anklicken und in neuem Fenster öffnen) Taschenrechner
(120°) (!150°) (60°)
(120°) (!90°) (240°)
(!50°) (!70°) (40°)
(!40°) (60°) (!240°)
(!30°) (90°) (270°)
(180°) (!45°) (90°)
|
|
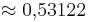 )
)
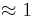 ) (!0) (0,5)
) (!0) (0,5)
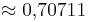 )
)
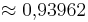 )
)
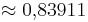 ) (
) (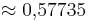 )
)
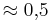 ) (0) (!1)
) (0) (!1)
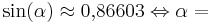
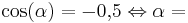
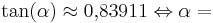
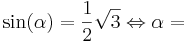
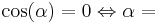
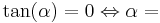
 Zurück zu 10. Klasse Algebra
Zurück zu 10. Klasse Algebra
