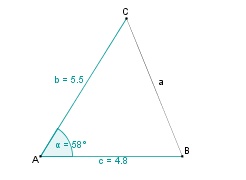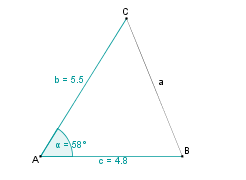SWS-Satz-3: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: Bild:Dreieck.png Lass uns nun die Konstruktionen und Beschreibungen vergleichen! <br /><br /> <div style="border: 2px solid #0000ee; background-color:#ffffff; padd...)
 
K
 
(14 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
 +
{{Navigation SSS und SWS}}
 +
 +
 
[[Bild:Dreieck.png]] Lass uns nun die Konstruktionen und Beschreibungen vergleichen!
 
[[Bild:Dreieck.png]] Lass uns nun die Konstruktionen und Beschreibungen vergleichen!
 
<br /><br />
 
<br /><br />
Zeile 6: Zeile 9:
 
{| class="wikitable"  
 
{| class="wikitable"  
 
|-  
 
|-  
−
| 1. || Wir beginnen mit der Grundseite c = 4,8 cm. || [[Bild:KS_Aufgabe_a1_SWS.png‎]]
+
| 1. || Zunächst fertigen wir eine Skizze an. || [[Bild:KS_Aufgabe_aPlanfigur_SWS.png‎‎]]
 
|-  
 
|-  
−
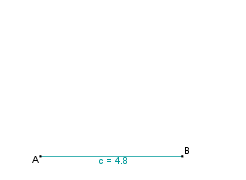
| 2. || Dann tragen wir den Winkel <math>\alpha</math> = 58° an A ab. || [[Bild:KS_Aufgabe_a2_SWS.png‎]]
+
| 2. || Wir beginnen mit der Grundseite c = 4,8 cm. || [[Bild:KS_Aufgabea1SWS.png]]
 +
|-
 +
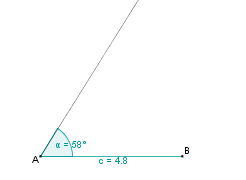
| 3. || Dann tragen wir den Winkel <math>\alpha</math> = 58° an A ab. || [[Bild:KS_Aufgabea2SWS.png‎]]
 
|-
 
|-
−
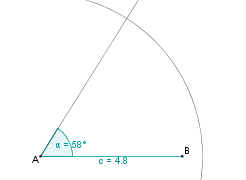
| 3. || Danach zeichnen wir einen Kreis mit Radius b = 5,5 cm um A. || [[Bild:KS_Aufgabe_a3_SWS.png‎]]
+
| 4. || Danach zeichnen wir einen Kreis mit Radius b = 5,5 cm um A. || [[Bild:KS_Aufgabea3SWS.png‎]]
 
|-
 
|-
−
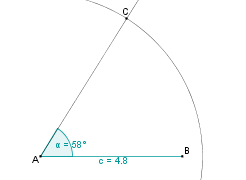
| 4. || Der Kreis schneidet die Halbgerade des Winkels im Punkt C. || [[Bild:KS_Aufgabe_a4_SWS.png‎]]
+
| 5. || Der Kreis schneidet die Halbgerade des Winkels im Punkt C. || [[Bild:KS_Aufgabea4SWS.png‎]]
 
|-
 
|-
−
| 5. || Wir verbinden die Punkte B und C. || [[Bild:KS_Aufgabe_a5_SWS.png‎]]
+
| 6. || Wir verbinden die Punkte B und C und erhalten ein eindeutig festgelegtes Dreieck. || [[Bild:KS_Aufgabea5SWS.png‎]]
 
|}
 
|}
  
Zeile 23: Zeile 28:
 
{| class="wikitable"  
 
{| class="wikitable"  
 
|-  
 
|-  
−
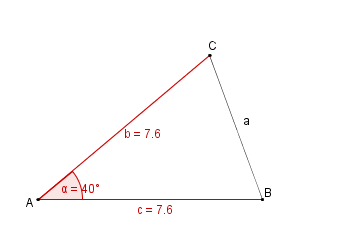
| 1. || Wir beginnen mit der Grundseite c = 7,6 cm. || [[Bild:KS_Aufgabe_b1_SWS.png‎]]
+
| 1. || Als erstes fertigen wir eine Skizze an, in der wir alle gegebenen Größen farbig markieren || [[Bild:KS_Aufgabe_bPlanfigur_SWS.png‎]]
 
|-  
 
|-  
−
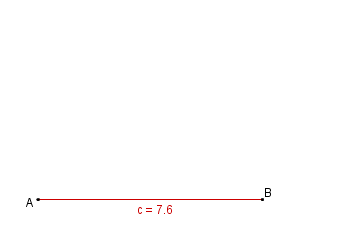
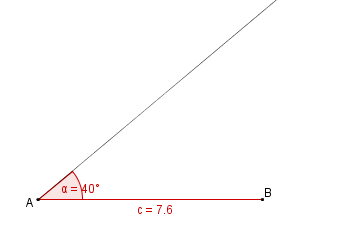
| 2. || Dann tragen wir den Winkel <math>\alpha</math> = 40° an A ab. || [[Bild:KS_Aufgabe_b2_SWS.png‎]]
+
| 2. || Wir beginnen mit der Grundseite c = 7,6 cm. || [[Bild:KS_Aufgabeb1SWS.png‎]]
 +
|-
 +
| 3. || Dann tragen wir den Winkel <math>\alpha</math> = 40° an A ab. || [[Bild:KS_Aufgabeb2SWS.png‎]]
 
|-
 
|-
−
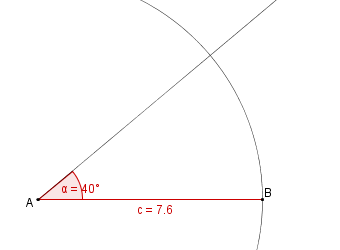
| 3. || Danach zeichnen wir einen Kreis mit Radius b = c = 7,6 cm um A. || [[Bild:KS_Aufgabe_b3_SWS.png‎]]
+
| 4. || Danach zeichnen wir einen Kreis mit Radius b = c = 7,6 cm um A. || [[Bild:KS_Aufgabeb3SWS.png‎]]
 
|-
 
|-
−
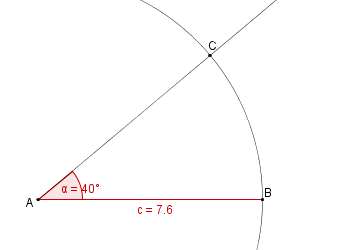
| 4. || Der Kreis schneidet die Halbgerade des Winkels im Punkt C. || [[Bild:KS_Aufgabe_b4_SWS.png‎]]
+
| 5. || Der Kreis schneidet die Halbgerade des Winkels im Punkt C. || [[Bild:KS_Aufgabeb4SWS.png‎]]
 
|-
 
|-
−
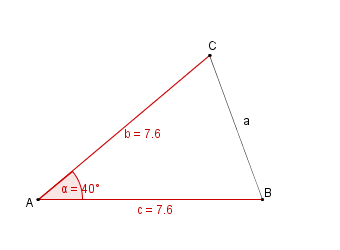
| 5. || Wir verbinden die Punkte B und C.  || [[Bild:KS_Aufgabe_b5_SWS.png‎]]
+
| 6. || Wir verbinden die Punkte B und C.  || [[Bild:KS_Aufgabeb5SWS.png‎]]
 
|}
 
|}
 
</div>
 
</div>
Zeile 39: Zeile 46:
 
{| class="wikitable"  
 
{| class="wikitable"  
 
|-  
 
|-  
−
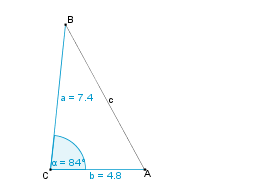
| 1. || Wir beginnen mit der Strecke [AC] = b = 4,8 cm. || [[Bild:KS_Aufgabe_c1_SWS.png‎]]
+
| 1. || Zunächst fertigen wir eine Skizze an und markieren alle gegebenen Größen farbig. || [[Bild:KS_Aufgabe_cPlanfigur_SWS.png‎]]
 
|-  
 
|-  
−
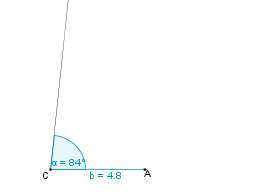
| 2. || Dann tragen wir den Winkel <math>\gamma</math> = 84° an C ab. || [[Bild:KS_Aufgabe_c2_SWS.png‎]]
+
| 2. || Wir beginnen mit der Strecke [AC] = b = 4,8 cm. || [[Bild:KS_Aufgabe_c1_SWS.png‎]]
 +
|-
 +
| 3. || Dann tragen wir den Winkel <math>\gamma</math> = 84° an C ab. || [[Bild:KS_Aufgabe_c2_SWS.png‎]]
 
|-
 
|-
−
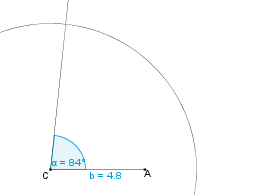
| 3. || Danach zeichnen wir einen Kreis mit Radius a = 7,4 cm um C. || [[Bild:KS_Aufgabe_c3_SWS.png‎]]
+
| 4. || Danach zeichnen wir einen Kreis mit Radius a = 7,4 cm um C. || [[Bild:KS_Aufgabe_c3_SWS.png‎]]
 
|-
 
|-
−
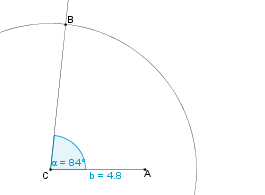
| 4. || Der Kreis schneidet die Halbgerade des Winkels im Punkt B. || [[Bild:KS_Aufgabe_c4_SWS.png‎]]
+
| 5. || Der Kreis schneidet die Halbgerade des Winkels im Punkt B. || [[Bild:KS_Aufgabe_c4_SWS.png‎]]
 
|-
 
|-
−
| 5. || Wir verbinden die Punkte A und B.  || [[Bild:KS_Aufgabe_c5_SWS.png‎]]
+
| 6. || Wir verbinden die Punkte A und B.  || [[Bild:KS_Aufgabe_c5_SWS.png‎]]
 
|}
 
|}
 
</div>
 
</div>
−
<br />
+
 
−
<div algin="left">[[Benutzer:Kathrin_Fuchs/SSS_und_SWS/weitere Aufgaben|<math>\Rightarrow</math> Wenn du jetzt noch Zeit hast, kannst du hier weitere Aufgaben zum SSS-Satz und SWS-Satz machen.]]</div>
+
[[Benutzer:Kathrin_Fuchs/SSS_und_SWS/Weitere Aufgaben|<math>\Rightarrow</math> Wenn du jetzt noch Zeit hast, kannst du hier weitere Aufgaben zum SSS-Satz und SWS-Satz machen.]]
−
<br />
+
 
−
Ansonsten geht es hier weiter zum 3.Lernpfad: [http://wikis.zum.de/dmuw/index.php/Benutzer:Kathrin_Fuchs/WSW_und_SSW_g WSW und SSW<sub>g</sub>]
+
Ansonsten geht es hier weiter zu einem der anderen beiden Lernpfade: <br />
 +
* [[Benutzer:Kathrin_Fuchs/Wiederholungen_zum_Dreieck | Wiederholungen zum Dreieck]]<br />
 +
* [[Benutzer:Kathrin_Fuchs/WSW_und_SSW_g | WSW-Satz und SSW<sub>g</sub>-Satz]]

Aktuelle Version vom 1. März 2010, 09:02 Uhr

Lernpfad SSS und SWS:   SSS-Satz - SSS: Aufgaben - SSS: Lösungen - SWS-Satz - SWS: Aufgaben - SWS: Lösungen - Weitere Aufgaben


Dreieck.png Lass uns nun die Konstruktionen und Beschreibungen vergleichen!

Konstruktionsbeschreibung zu a) mit c = 4,8 cm, b = 5,5 cm, 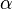\alpha = 58°

1. Zunächst fertigen wir eine Skizze an. KS Aufgabe aPlanfigur SWS.png
2. Wir beginnen mit der Grundseite c = 4,8 cm. KS Aufgabea1SWS.png
3. Dann tragen wir den Winkel \alpha = 58° an A ab. KS Aufgabea2SWS.png
4. Danach zeichnen wir einen Kreis mit Radius b = 5,5 cm um A. KS Aufgabea3SWS.png
5. Der Kreis schneidet die Halbgerade des Winkels im Punkt C. KS Aufgabea4SWS.png
6. Wir verbinden die Punkte B und C und erhalten ein eindeutig festgelegtes Dreieck. KS Aufgabea5SWS.png


Konstruktionsbeschreibung zu b) mit c = 7,6 cm, b = c, 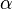\alpha = 40°

1. Als erstes fertigen wir eine Skizze an, in der wir alle gegebenen Größen farbig markieren KS Aufgabe bPlanfigur SWS.png
2. Wir beginnen mit der Grundseite c = 7,6 cm. KS Aufgabeb1SWS.png
3. Dann tragen wir den Winkel \alpha = 40° an A ab. KS Aufgabeb2SWS.png
4. Danach zeichnen wir einen Kreis mit Radius b = c = 7,6 cm um A. KS Aufgabeb3SWS.png
5. Der Kreis schneidet die Halbgerade des Winkels im Punkt C. KS Aufgabeb4SWS.png
6. Wir verbinden die Punkte B und C. KS Aufgabeb5SWS.png


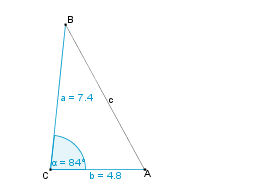
Konstruktionsbeschreibung zu c) a = 7,4 cm, b = 4,8 cm, 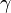\gamma = 84°

1. Zunächst fertigen wir eine Skizze an und markieren alle gegebenen Größen farbig. KS Aufgabe cPlanfigur SWS.png
2. Wir beginnen mit der Strecke [AC] = b = 4,8 cm. KS Aufgabe c1 SWS.png
3. Dann tragen wir den Winkel \gamma = 84° an C ab. KS Aufgabe c2 SWS.png
4. Danach zeichnen wir einen Kreis mit Radius a = 7,4 cm um C. KS Aufgabe c3 SWS.png
5. Der Kreis schneidet die Halbgerade des Winkels im Punkt B. KS Aufgabe c4 SWS.png
6. Wir verbinden die Punkte A und B. KS Aufgabe c5 SWS.png

\Rightarrow Wenn du jetzt noch Zeit hast, kannst du hier weitere Aufgaben zum SSS-Satz und SWS-Satz machen.

Ansonsten geht es hier weiter zu einem der anderen beiden Lernpfade:

Von „http://dmuw.zum.de/index.php?title=Benutzer:Kathrin_Fuchs/SSS_und_SWS/SWS-Satz-3&oldid=17696“