WSW-Satz-1: Unterschied zwischen den Versionen
Aus DMUW-Wiki
K (Die Seite wurde neu angelegt: <div style="border: 2px solid #0000ee; background-color:#ffffff; padding:7px;"> {| class="wikitable" |- | Bild:KS_Dreieck2.JPG || Wie konstruiert man ein Drei...) |
K |
||
| (4 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | {{Navigation WSW und SsW}} | ||
| + | |||
| + | |||
<div style="border: 2px solid #0000ee; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid #0000ee; background-color:#ffffff; padding:7px;"> | ||
{| class="wikitable" | {| class="wikitable" | ||
| Zeile 8: | Zeile 11: | ||
''Anmerkung: Es gilt <math>\alpha</math> + <math>\beta</math> + <math>\gamma</math> <math>=</math> 180°. Somit kann das Maß des dritten Winkels berechnet werden.<br />Deshalb ist die Konstruktion eines Dreiecks, von dem eine Seitenlänge und zwei Innenwinkelmaße gegeben sind, <u>IMMER</u> möglich.'' | ''Anmerkung: Es gilt <math>\alpha</math> + <math>\beta</math> + <math>\gamma</math> <math>=</math> 180°. Somit kann das Maß des dritten Winkels berechnet werden.<br />Deshalb ist die Konstruktion eines Dreiecks, von dem eine Seitenlänge und zwei Innenwinkelmaße gegeben sind, <u>IMMER</u> möglich.'' | ||
</div> | </div> | ||
| + | <br /> | ||
| + | <div style="border: 2px solid #0000ee; background-color:#ffffff; padding:7px;"> | ||
| + | {| class="wikitable" | ||
| + | |- | ||
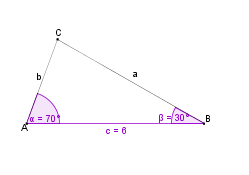
| + | | Um das Dreieck zu konstruieren fertigen wir zunächst eine Skizze an. Dazu zeichnen wir ein beliebiges Dreieck und markieren alle gegebenen Größen farbig. || [[Bild:KS_Planfigur_WSW.png]] | ||
| + | |- | ||
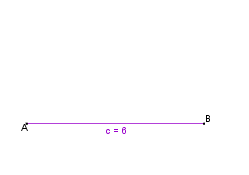
| + | | Wir beginnen mit der Grundseite c = 6 cm. || [[Bild:KS Schritt1 WSW.png]] | ||
| + | |- | ||
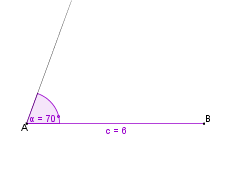
| + | | Am Punkt A tragen wir den Winkel <math>\alpha</math><math>=</math>70° <u>''gegen den Uhrzeigersinn''</u> ab. || [[Bild:KS Schritt2 WSW.png]] | ||
| + | |- | ||
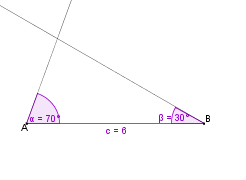
| + | | Am Punkt B tragen wir den Winkel <math>\beta</math><math>=</math>30° <u>''im Uhrzeigersinn''</u> ab. <br /><br /><small>VORSICHT: Klicke zuerst auf den Punkt A, dann auf den Punkt B und gib dann die Winkelgröße an.<br />Vergiss nicht die '''RICHTUNG''' des Winkels zu ändern!!</small> || [[Bild:KS Schritt3 WSW.png]] | ||
| + | |- | ||
| + | | Die Halbgeraden der Winkel schneiden sich im Punkt C. || [[Bild:KS Schritt4 WSW.png]] | ||
| + | |- | ||
| + | | Somit erhalten ein eindeutig festgelegtes Dreieck. || [[Bild:KS Schritt5 WSW.png]] | ||
| + | |} | ||
| + | </div> | ||
<br /> | <br /> | ||
| − | < | + | <br /> |
| + | {{Merke| | ||
| + | '''WSW-Satz'''<br /> | ||
| + | Dreiecke sind zueinander '''kongruent''', wenn sie in der Länge von '''einer Seite''' und den Maßen der beiden '''anliegenden Winkel''' übereinstimmen (Winkel-Seite-Winkel-Satz). | ||
| + | <br />''<u>oder:</u>'' Man kann ein Dreieck eindeutig konstruieren wenn die Länge einer Seite und die Maße der beiden anliegenden Winkel gegeben sind. | ||
| + | }} | ||
| + | {{Aufgabe-Mathe|Übertrage den Satz auf deinen <u>Laufzettel</u>!}} | ||
| + | <br /> | ||
| + | <br /> | ||
| + | [[Benutzer:Kathrin_Fuchs/WSW_und_SSW_g/WSW-Satz-2|<math>\Rightarrow</math> Wenn du den Satz abgeschrieben hast, gibt es hier eine Aufgabe dazu.]] | ||
Aktuelle Version vom 19. Februar 2010, 22:10 Uhr
Lernpfad WSW und SSWg: WSW-Satz - WSW: Aufgaben - WSW: Lösungen - SsW-Satz - SsW: Aufgaben - SsW: Lösungen - Weitere Aufgaben
 |
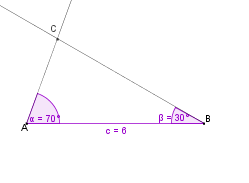
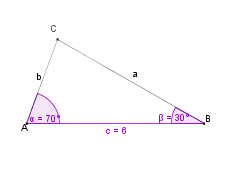
Wie konstruiert man ein Dreieck, von dem die Länge einer Seite und die Maße der beiden anliegenden Winkel gegeben sind? |
Wir wollen ein Dreieck konstruieren, von dem die Seite c = 6 cm,
sowie die anliegenden Winkel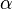 
70° und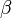 
30° gegeben sind.
Anmerkung: Es gilt + +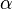 
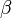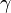
180°. Somit kann das Maß des dritten Winkels berechnet werden.
Deshalb ist die Konstruktion eines Dreiecks, von dem eine Seitenlänge und zwei Innenwinkelmaße gegeben sind, IMMER möglich.
| Um das Dreieck zu konstruieren fertigen wir zunächst eine Skizze an. Dazu zeichnen wir ein beliebiges Dreieck und markieren alle gegebenen Größen farbig. | 
|
| Wir beginnen mit der Grundseite c = 6 cm. | 
|
| Am Punkt A tragen wir den Winkel 70° gegen den Uhrzeigersinn ab. |
|
| Am Punkt B tragen wir den Winkel 30° im Uhrzeigersinn ab. VORSICHT: Klicke zuerst auf den Punkt A, dann auf den Punkt B und gib dann die Winkelgröße an. Vergiss nicht die RICHTUNG des Winkels zu ändern!! |
|
| Die Halbgeraden der Winkel schneiden sich im Punkt C. | 
|
| Somit erhalten ein eindeutig festgelegtes Dreieck. | 
|
 Merke
WSW-Satz |
Aufgabe
Übertrage den Satz auf deinen Laufzettel! |
Wenn du den Satz abgeschrieben hast, gibt es hier eine Aufgabe dazu.
