Übungen zu a: Unterschied zwischen den Versionen
(Änderung 17901 von Isabell Vogel (Diskussion) wurde rückgängig gemacht.) |
|||
| (3 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 10: | Zeile 10: | ||
| − | Hilfe {{versteckt| | + | Hilfe {{versteckt|1= |
| − | + | <br\> | |
| − | + | ||
Ist '''a = 1''' heißt der dazugehörige Graph '''Normalparabel'''. <br\> | Ist '''a = 1''' heißt der dazugehörige Graph '''Normalparabel'''. <br\> | ||
Ist '''a > 1''', dann ist die Parabel enger ('''gestreckt''') als die Normalparabel.<br\> | Ist '''a > 1''', dann ist die Parabel enger ('''gestreckt''') als die Normalparabel.<br\> | ||
Für '''0 < a < 1''' ist die Parabel weiter ('''gestaucht''') als die Normalparabel.<br\> | Für '''0 < a < 1''' ist die Parabel weiter ('''gestaucht''') als die Normalparabel.<br\> | ||
| − | Ist a '''negativ''', so ist die Parabel '''nach unten geöffnet'''. | + | Ist a '''negativ''', so ist die Parabel '''nach unten geöffnet'''.<br\> |
| − | + | <br\> | |
}} | }} | ||
| Zeile 76: | Zeile 75: | ||
[[Bild:Laufzettel.png|50px]] Bewerte erst die Aufgaben deinem Laufzettel, bevor du weitermachst! | [[Bild:Laufzettel.png|50px]] Bewerte erst die Aufgaben deinem Laufzettel, bevor du weitermachst! | ||
<br\> | <br\> | ||
| − | + | <br\> | |
| − | <div algin="left">[[Variationen/Quadratische Funktionen2/Quadratische Funktionen und der Parameter c|<math>\Rightarrow</math> nächstes Kapitel]]</div> | + | <big><div algin="left">[[Variationen/Quadratische Funktionen2/Quadratische Funktionen und der Parameter c|<math>\Rightarrow</math> nächstes Kapitel]]</div></big> |
| + | <br\> | ||
<br\> | <br\> | ||
<div align="left">[[Variationen/Quadratische Funktionen2|<math>\Leftarrow</math> Zurück zur Übersicht]]</div> | <div align="left">[[Variationen/Quadratische Funktionen2|<math>\Leftarrow</math> Zurück zur Übersicht]]</div> | ||
Aktuelle Version vom 15. März 2010, 18:08 Uhr
Aufgabe 7
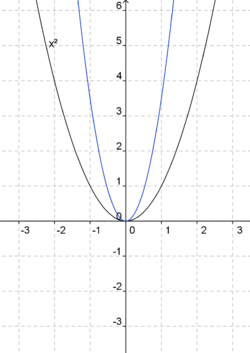
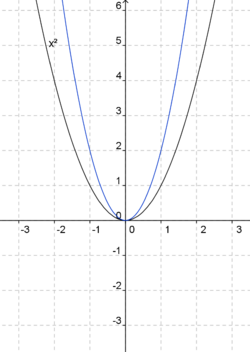
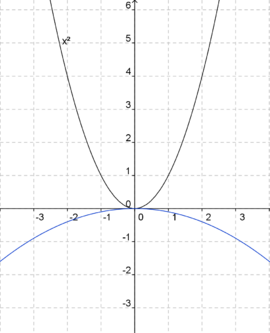
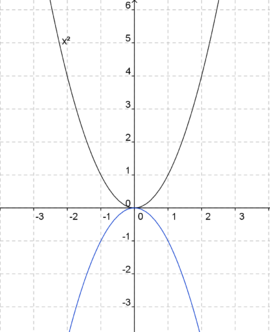
In den Funktionsgleichungen unten hat a bereits einen bestimmten Wert angenommen. Ordne den blaugefärbten Parabeln die jeweils richtige Gleichung zu. Die Normalparabel (schwarz) dient dir als Orientierung.
Hilfe
Ist a = 1 heißt der dazugehörige Graph Normalparabel.
Ist a > 1, dann ist die Parabel enger (gestreckt) als die Normalparabel.
Für 0 < a < 1 ist die Parabel weiter (gestaucht) als die Normalparabel.
Ist a negativ, so ist die Parabel nach unten geöffnet.
.
Aufgabe 8
Kreuze die zutreffenden Aussagen zu obigen quadratischen Funktionen an. Es sind jeweils mehrere Antworten richtig.
f(x) = 3,5x2 (!Die Parabel ist nach unten geöffnet.) (Die Parabel ist nach oben geöffnet.) (Die Parabel ist enger als die Normalparabel.) (!Die Parabel ist weiter als die Normalparabel.) (Der Punkt [2|14] liegt auf dem Graphen.) (Der Punkt [14|2] liegt nicht auf dem Graphen.)
f(x) = -x2 (Die Parabel ist nach unten geöffnet.) (!Die Parabel ist nach oben geöffnet.) (!Die Parabel ist enger als die Normalparabel.) (!Die Parabel ist weiter als die Normalparabel.) (Der Punkt [1|-1] liegt auf dem Graphen.) (!Der Punkt [2|2] liegt auf dem Graphen.)
f(x) = 2x2 (!Die Parabel ist nach unten geöffnet.) (Die Parabel ist nach oben geöffnet.) (Die Parabel ist enger als die Normalparabel.) (!Die Parabel ist weiter als die Normalparabel.) (!Der Punkt [0|-2] liegt auf dem Graphen.) (Der Punkt [1|2] liegt auf dem Graphen.)
f(x) = -0,1x2 (Die Parabel ist nach unten geöffnet.) (!Die Parabel ist nach oben geöffnet.) (!Die Parabel ist enger als die Normalparabel.) (Die Parabel ist weiter als die Normalparabel.) (!Der Punkt [-1|2] liegt auf dem Graphen.) (Der Punkt [-1|1] liegt oberhalb des Graphen.)
.
Bevor wir zum nächsten Kapitel gehen, hast du hier noch einmal die Möglichkeit alles wichtige zusammengefasst zu wiederholen:
|
Merke:
Die Graphen von Funktionen mit der Funktionsgleichung Sie sind symmetrisch zur y-Achse. Der Punkt Ist a = 1 heißt der dazugehörige Graph Normalparabel. |
Alles klar? Dann kann's ja weitergehen.
![]() Bewerte erst die Aufgaben deinem Laufzettel, bevor du weitermachst!
Bewerte erst die Aufgaben deinem Laufzettel, bevor du weitermachst!
 3,5 x2
3,5 x2 
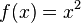 heißen Parabeln.
heißen Parabeln.
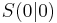 heißt Scheitel der Parabel und ist der tiefste Punkt.
heißt Scheitel der Parabel und ist der tiefste Punkt.
 nächstes Kapitel
nächstes Kapitel Zurück zur Übersicht
Zurück zur Übersicht
