Vierstreckensatz: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
(Links eingefügt)
(Links angepasst)
 
(20 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt)
Zeile 9: Zeile 9:
 
<br>
 
<br>
 
<br>
 
<br>
−
:'''In diesem Lernpfad durchläufst du 7 Stationen. Sie sind wie folgt gegliedert:'''<br>
+
:'''In diesem Lernpfad durchläufst du 5 Stationen. Sie sind wie folgt gegliedert:'''<br>
  
 
:1. Station: Erster Vierstreckensatz - Schenkellösung<br>
 
:1. Station: Erster Vierstreckensatz - Schenkellösung<br>
−
:[[Benutzer:Leonie Porzelt/Vierstreckensatz/2.Station|2. Station: Erster Vierstreckensatz - Abschnittlösung]]<br>  
+
:[[/2.Station|2. Station: Erster Vierstreckensatz - Abschnittlösung]]<br>  
−
:[[Benutzer:Leonie Porzelt/Vierstreckensatz/3.Station|3. Station: Zweiter Vierstreckensatz]]<br>
+
:[[/3.Station|3. Station: Zweiter Vierstreckensatz]]<br>
−
:[[Benutzer:Leonie Porzelt/Vierstreckensatz/4.Station|4. Station: Zusammenfassung]]<br>
+
:[[/4.Station|4. Station: Zusammenfassung]]<br>
−
:[[Benutzer:Leonie Porzelt/Vierstreckensatz/5.Station|5. Station: Übung]]<br>
+
:[[/5.Station|5. Station: Übung]]<br>
  
  
Zeile 30: Zeile 30:
 
<br>
 
<br>
 
==1. Station: Erster Vierstreckensatz - Schenkellösung==
 
==1. Station: Erster Vierstreckensatz - Schenkellösung==
−
[[Bild:Porzelt_Laptop.jpg]]
+
[[Bild:Porzelt_Laptop.jpg]]<br>
−
:'''Zoll''' ist eine '''Längeneinheit''' die im Alltag häufig zu finden ist, z.B. bei Laptops, Computern und Fernsehern.  
+
'''Zoll''' ist eine '''Längeneinheit''', die im Alltag häufig zu finden ist, z.B. bei Laptops, Computern und Fernsehern. <br>
−
:Um sich die Größe besser vorstellen zu können, soll die Einheit Zoll in Zentimeter umgerechnet werden.  
+
Um sich die Größe besser vorstellen zu können, soll die Einheit Zoll in Zentimeter umgerechnet werden. <br>
−
:Hierfür gibt es zwei Möglichkeiten:
+
Hierfür gibt es zwei Möglichkeiten:<br>
−
:*die algebraische Berechnung
+
*die algebraische Berechnung<br>
−
:*oder die geometrische.
+
*oder die geometrische.<br>
−
:Als Bepsiel nehmen wir die Umrechnung von einem 15 Zoll Laptop.
+
Als Bepsiel nehmen wir die Umrechnung von einem 15-Zoll-Laptop.<br>
 
<br>
 
<br>
 
*Finde heraus wie du die Aufgabe '''algebraisch''' lösen kannst:  
 
*Finde heraus wie du die Aufgabe '''algebraisch''' lösen kannst:  
−
::'''Gegeben''': Der Laptop hat einen 15 Zoll Bildschirm. 1 Zoll entspricht 2,54 cm.
+
<div style="border: 2px solid #00cd00; background-color:#ffffff; padding:7px;">
−
::'''Gesucht''': Umrechnung von 15 Zoll in cm.
+
:'''Gegeben''': Der Laptop hat einen 15 Zoll Bildschirm. 1 Zoll entspricht 2,54 cm.
−
::'''Lösung''': Berechne in deinem Heft und trage hier deine Lösung mit Angabe der Einheit (cm) ein!  
+
:'''Gesucht''': Umrechnung von 15 Zoll in cm.
−
::::(Bitte mach ein Leerzeichen zwischen Zahl und Einheit.)
+
:'''Lösung''': Berechne in deinem Heft und trage hier deine Lösung mit Angabe der Einheit (cm) ein!  
 +
:::(Bitte mach ein Leerzeichen zwischen Zahl und Einheit.)
 
<div class="lueckentext-quiz">
 
<div class="lueckentext-quiz">
 
15 Zoll entsprechen '''38,1 cm (Tipp:  Berechne mit Hilfe des Dreisatzes)'''.
 
15 Zoll entsprechen '''38,1 cm (Tipp:  Berechne mit Hilfe des Dreisatzes)'''.
 +
</div>
 +
&nbsp;
 
</div>
 
</div>
 
<br>
 
<br>
Zeile 55: Zeile 58:
 
'''Klicke die Schritte nacheinander an:'''<br>
 
'''Klicke die Schritte nacheinander an:'''<br>
 
1. Schritt: Zeichne zwei Halbgeraden mit gemeinsamen Anfangspunkt Z und trage auf diesen Halbgeraden <br>
 
1. Schritt: Zeichne zwei Halbgeraden mit gemeinsamen Anfangspunkt Z und trage auf diesen Halbgeraden <br>
−
:die Längen 1 cm und 15 cm ab. Benenne die Endpunkte der Strecken mit A und B. <br>
+
:die Längen 1 cm und 15 cm ab! Benenne die Endpunkte der Strecken mit A und B! <br>
−
2. Schritt: Verbinde Punkt A mit Punkt B.<br>
+
2. Schritt: Verbinde Punkt A mit Punkt B!<br>
−
3. Schritt: Trage in Z die Strecke [ZA'] mit <span style="text-decoration: overline;">ZA'</span> = 2,54 cm ab. <br>
+
3. Schritt: Trage in Z die Strecke [ZA'] mit <span style="text-decoration: overline;">ZA'</span> = 2,54 cm ab! <br>
−
4. Schritt: Zeichne eine Parallele durch A' zu [AB].<br>
+
4. Schritt: Zeichne eine Parallele durch A' zu [AB]!<br>
−
5. Schritt: Benenne Schnittpunkt mit B'. <br>
+
5. Schritt: Benenne Schnittpunkt mit B'! <br>
−
6. Schritt: Miss <span style="text-decoration: overline;">ZB'</span> ab.  
+
6. Schritt: Miss <span style="text-decoration: overline;">ZB'</span> ab!  
 
<ggb_applet height="300" width="950" showResetIcon="true" filename="Porzelt_geometrisch.ggb" />
 
<ggb_applet height="300" width="950" showResetIcon="true" filename="Porzelt_geometrisch.ggb" />
 
</div>   
 
</div>   
 
<br>
 
<br>
−
:'''Die Rechnung die dahinter steckt:'''
+
'''Die Rechnung, die dahinter steckt:'''<br>
−
:Vorrausgesetzt wird dass die Gerade '''A'B' zu AB parallel''' ist. Das '''Dreieck A'ZB'''' kann somit als das '''Bild''' des '''Dreiecks AZB (Urbild)'''
+
Vorausgesetzt wird, dass die Gerade '''A'B' zu AB parallel''' ist. Das '''Dreieck A'ZB'''' kann somit als das '''Bild''' des '''Dreiecks AZB (Urbild)'''<br>
−
:mit dem Streckungszentrum Z aufgefasst werden. Der Punkt '''A''' wurde also '''auf''' den Punkt '''A'''' und Punkt '''B''' wurde '''auf''' Punkt '''B' abgebildet'''.  
+
mit dem Streckungszentrum Z aufgefasst werden. Der Punkt '''A''' wurde also '''auf''' den Punkt '''A'''' und Punkt '''B''' wurde '''auf''' Punkt '''B' abgebildet'''. <br>
−
:Aus dem vorherigen Lernpfad wissen wir, dass das '''Längenverhältnis von Strecken''' bei einer zentrischen Streckung, wegen der <br>Eigenschaft der '''Längenverhältnistreue''', '''gleich''' ist.  
+
Aus dem vorherigen Lernpfad wissen wir, dass das '''Längenverhältnis von Strecken''' bei einer zentrischen Streckung, wegen der <br>Eigenschaft der '''Längenverhältnistreue''', '''gleich''' ist. <br>
−
:'''Was bedeutet dies?''' Eine kleine Wiederholung kann nicht schaden. Setze dafür die richtige Aussage in die passende Lücke ein:
+
'''Was bedeutet dies?''' Eine kleine Wiederholung kann nicht schaden. Setze dafür die richtige Aussage in die passende Lücke ein:
−
<div class="lueckentext-quiz">
+
<div style="border: 2px solid #0000ff; background-color:#ffffff; padding:7px;">
−
<math>\overline{ZA'}</math> = '''|k| ∙ <math>\overline{ZA}</math>''' <math>\wedge</math> <math>\overline{ZB'}</math> = '''|k| ∙ <math>\overline{ZB}</math>'''<br>
+
<div class="lueckentext-quiz"><br>
 +
<math>\overline{ZA'}</math> = '''<math>\mid k\mid  \cdot \overline{ZA}</math>''' <math>\mathit{und}\ </math> <math>\overline{ZB'} =</math> '''<math>\mid k \mid \cdot \overline{ZB}</math>'''<br>
 
Aufgelöst nach |k|:<br>
 
Aufgelöst nach |k|:<br>
−
|k| = '''<math>{\overline{ZA'}\over\overline{ZA}}</math>''' <math>\wedge</math> '''|k|''' = <math>{\overline{ZB'}\over\overline{ZB}}</math><br>
+
<math>\mid k \mid =</math> '''<math>{\overline{ZA'}\over\overline{ZA}}</math>''' <math>\mathit{und}\ </math> '''<math>\mid k \mid</math>''' <math>= {\overline{ZB'}\over\overline{ZB}}</math><br>
 
Gleichsetzen:
 
Gleichsetzen:
−
<math>{\overline{ZA'}\over\overline{ZA}}</math> = <math>{\overline{ZB'}\over\overline{ZB}}</math><br>
+
<math>{\overline{ZA'}\over\overline{ZA}} =</math> <math>{\overline{ZB'}\over\overline{ZB}}</math><br>
 
Einsetzen der Werte ergibt: <br>
 
Einsetzen der Werte ergibt: <br>
−
'''<math>{2,54 cm}\over{1 Zoll}</math>''' = <math>{x cm}\over{15 Zoll}</math> <math>\Rightarrow</math> x = 38,1 cm
+
<math>{{2,54\ cm}\over{1\ Zoll}} =</math> '''<math>{x}\over{15\ Zoll}</math>''' <math>\Rightarrow x = 38,1\ cm</math>
 
</div>
 
</div>
−
<br>
+
&nbsp;
−
:Prima! Du hast dein Wissen noch einmal aufgefrischt!
+
−
<div style="border: 2px solid #ffd700; background-color:#ffffff; padding:7px;">
+
−
:Die Formel sagt aus, dass sich die Abschnitte auf der einen Halbgeraden genauso verhalten, wie die Abschnitte auf der anderen
+
−
:Halbgeraden. Diesen Satz nennt man den '''ersten Vierstreckensatz'''. In unserem Beispiel wurden die Schenkel betrachtet,
+
−
:deshalb wird es auch die '''Schenkellösung''' genannt.
+
 
</div>
 
</div>
 
<br>
 
<br>
−
 
+
[[Bild:Porzelt_lobenderPanto8.jpg]]
−
==2. Station: Erster Vierstreckensatz - Abschnittlösung==
+
−
[[Bild:Porzelt_Vierstreckensatz_Abschnittlösung.jpg]]
+
−
:Anhand der Eigenschaft der Längenverhältnisstreue der zentrischen Streckung, kannst du auch hier wieder die geeignete Formel
+
−
:zur Berechnung der unbekannten Strecke herleiten. Setze dafür die richtige Aussage in die passende Lücke ein:
+
−
<div class="lueckentext-quiz">
+
−
<math>\overline{AA'}</math> = '''|k| ∙ <math>\overline{ZA}</math> - <math>\overline{ZA}</math>''' <math>\wedge</math> <math>\overline{BB'}</math> = '''|k| ∙ <math>\overline{ZB}</math> - <math>\overline{ZB}</math>'''<br>
+
−
Aufgelöst nach |k|:<br>
+
−
|k| = '''<math>{\overline{AA'}\over\overline{ZA}}</math>''' - <math>{\overline{ZA}\over\overline{ZA}}</math> <math>\wedge</math> |k| = <math>{\overline{BB'}\over\overline{ZB}}</math> - '''<math>{\overline{ZB}\over\overline{ZB}}</math>'''<br>
+
−
|k| = '''<math>{\overline{AA'}\over\overline{ZA}}</math> - 1''' <math>\wedge</math> '''|k|''' = <math>{\overline{BB'}\over\overline{ZB}}</math> - 1<br>
+
−
Gleichsetzen:<br>
+
−
<math>{\overline{AA'}\over\overline{ZA}}</math> - '''1''' = '''<math>{\overline{BB'}\over\overline{ZB}}</math> '''- 1 '''|+1'''<br>
+
−
<math>{\overline{AA'}\over\overline{ZA}}</math> = <math>{\overline{BB'}\over\overline{ZB}}</math>
+
−
</div>
+
−
:Super! Du hast hier die '''Abschnittlösung des ersten Vierstreckensatzes''' hergeleitet. Denn auch hier verhalten sich die
+
−
:Abschnitte auf der einen Halbgeraden, wie die Abschnitte auf der anderen Halbgeraden.
+
−
:Berechne nun die Aufgabe in deinem Heft und trage hier deine Lösung mit Angabe der Einheit (cm) ein!
+
−
<div class="lueckentext-quiz">
+
−
x= '''1 cm (Tipp:  Leerzeichen zwischen Zahl und Einheit nicht vergessen!)'''.
+
−
</div>
+
 
<br>
 
<br>
−
 
+
<div style="border: 2px solid #ffd700; background-color:#ffffff; padding:7px;">
−
==3. Station: Zweiter Vierstreckensatz==
+
[[Bild:Porzelt_Panto-2.jpg|left]]
−
[[Bild:Porzelt_4-Streckensatz-Kletterwand.jpg]]
+
Die Formel sagt aus, dass sich die Abschnitte auf der einen Halbgeraden genauso verhalten wie die Abschnitte auf der anderen <br>
−
:Auf dem Bild siehst du Panto neben einer 6 m hohen Kletterwand. Auch hier musst du wieder eine passende Formel zur
+
Halbgeraden. Diesen Satz nennt man den '''ersten Vierstreckensatz'''. In unserem Beispiel wurden die Schenkel betrachtet, <br>
−
:Berechnung der gesuchten Strecke x herleiten. Setze wieder die richtige Aussage in die passende Lücke ein:
+
deshalb wird es auch die '''Schenkellösung''' genannt.<br>
−
<div class="lueckentext-quiz">
+
−
<math>\overline{ZA'}</math> = '''|k| ∙ <math>\overline{ZA}</math>''' <math>\wedge</math> <math>\overline{A'B'}</math> = '''|k| ∙ <math>\overline{AB}</math>'''<br>
+
−
Aufgelöst nach |k|:<br>
+
−
|k| = '''<math>{\overline{ZA'}\over\overline{ZA}}</math>''' <math>\wedge</math> '''|k|''' = <math>{\overline{A'B'}\over\overline{AB}}</math><br>
+
−
Gleichsetzen:
+
−
<math>{\overline{ZA'}\over\overline{ZA}}</math> = <math>{\overline{A'B'}\over\overline{AB}}</math><br>
+
 
</div>
 
</div>
−
:Fantastisch! Du hast hier den '''zweiten Vierstreckensatz''' hergeleitet. Er sagt aus, dass sich die Streckenabschnitte auf den
 
−
:Parallelen, wie die zugehörigen Streckenlängen (von Z ausgehend) auf einer Geraden verhalten.
 
−
:Berechne jetzt die Aufgabe in deinem Heft und trage hier deine Lösung mit Angabe der Einheit (cm) ein!
 
−
<div class="lueckentext-quiz">
 
−
x= '''0,30 cm (Tipp:  Leerzeichen zwischen Zahl und Einheit nicht vergessen!)'''.
 
−
</div>
 
−
:Wenn du wissen willst, ob es Panto auf die Kletterwand geschafft hat, dann lass es dir anzeigen.
 
−
:{{Versteckt|
 
−
[[Bild:Porzelt_4-Streckensatz-Kletterwand-Lösung.jpg]]|}}
 
 
<br>
 
<br>
−
 
+
<div align="left">[[Lernpfade/Zentrische Streckung/Vierstreckensatz/2.Station|<math>\Rightarrow</math> Weiter zur 2. Station: Erster Vierstreckensatz - Abschnittlösung]]</div>
−
==4. Station: Zusammenfassung==
+
−
:Hier ist alles was du bisher herausgefunden hast kurz zusammengefasst. Übertrage diese Zusammenfassung in dein Heft.
+
−
<div style="border: 2px solid #FF0000; background-color:#ffffff; padding:7px;">
+
−
====Ausgangsfigur====
+
−
Zwei Strahlen s<sub>1</sub> und s<sub>2</sub> mit gemeinsamen Scheitelpunkt Z und zwei Parallelen p<sub>1</sub> und p<sub>2</sub>,
+
−
die beide Strahlen schneiden.
+
−
<br>
+
−
====1. Vierstreckensatz (Schenkellösung)====
+
−
{|
+
−
|[[Bild:Porzelt_1a_Strahlensatz.jpg]]||<math>{\overline{ZA'}\over\overline{ZA}}</math> = <math>{\overline{ZB'}\over\overline{ZB}}</math>
+
−
|}
+
−
<br>
+
−
====1. Vierstreckensatz (Abschnittlösung)====
+
−
{|
+
−
|[[Bild:Porzelt_1b_Strahlensatz.jpg]]||<math>{\overline{AA'}\over\overline{ZA}}</math> = <math>{\overline{BB'}\over\overline{ZB}}</math>
+
−
|}
+
−
<br>
+
−
====2. Vierstreckensatz====
+
−
{|
+
−
|[[Bild:Porzelt_2_Strahlensatz.jpg]]||<math>{\overline{ZA'}\over\overline{ZA}}</math> = <math>{\overline{A'B'}\over\overline{AB}}</math> oder <math>{\overline{ZB'}\over\overline{ZB}}</math> = <math>{\overline{A'B'}\over\overline{AB}}</math>
+
−
|}
+
−
</div>
+
−
<br>
+
−
 
+
−
==5. Station: Übung==
+

Aktuelle Version vom 19. Dezember 2009, 15:55 Uhr


Mathematik-digital Pfeil-3d.png
Lernpfad

Vierstreckensatz


Porzelt Vierstreckensatz.jpg





In diesem Lernpfad durchläufst du 5 Stationen. Sie sind wie folgt gegliedert:
1. Station: Erster Vierstreckensatz - Schenkellösung
2. Station: Erster Vierstreckensatz - Abschnittlösung
3. Station: Zweiter Vierstreckensatz
4. Station: Zusammenfassung
5. Station: Übung












1. Station: Erster Vierstreckensatz - Schenkellösung

Porzelt Laptop.jpg
Zoll ist eine Längeneinheit, die im Alltag häufig zu finden ist, z.B. bei Laptops, Computern und Fernsehern.
Um sich die Größe besser vorstellen zu können, soll die Einheit Zoll in Zentimeter umgerechnet werden.
Hierfür gibt es zwei Möglichkeiten:

  • die algebraische Berechnung
  • oder die geometrische.

Als Bepsiel nehmen wir die Umrechnung von einem 15-Zoll-Laptop.

  • Finde heraus wie du die Aufgabe algebraisch lösen kannst:
Gegeben: Der Laptop hat einen 15 Zoll Bildschirm. 1 Zoll entspricht 2,54 cm.
Gesucht: Umrechnung von 15 Zoll in cm.
Lösung: Berechne in deinem Heft und trage hier deine Lösung mit Angabe der Einheit (cm) ein!
(Bitte mach ein Leerzeichen zwischen Zahl und Einheit.)

15 Zoll entsprechen 38,1 cm (Tipp: Berechne mit Hilfe des Dreisatzes).

 




  • Im Folgenden wird dir gezeigt, wie du die Aufgabe geometrisch lösen kannst.


Klicke die Schritte nacheinander an:
1. Schritt: Zeichne zwei Halbgeraden mit gemeinsamen Anfangspunkt Z und trage auf diesen Halbgeraden

die Längen 1 cm und 15 cm ab! Benenne die Endpunkte der Strecken mit A und B!

2. Schritt: Verbinde Punkt A mit Punkt B!
3. Schritt: Trage in Z die Strecke [ZA'] mit ZA' = 2,54 cm ab!
4. Schritt: Zeichne eine Parallele durch A' zu [AB]!
5. Schritt: Benenne Schnittpunkt mit B'!
6. Schritt: Miss ZB' ab!


Die Rechnung, die dahinter steckt:
Vorausgesetzt wird, dass die Gerade A'B' zu AB parallel ist. Das Dreieck A'ZB' kann somit als das Bild des Dreiecks AZB (Urbild)
mit dem Streckungszentrum Z aufgefasst werden. Der Punkt A wurde also auf den Punkt A' und Punkt B wurde auf Punkt B' abgebildet.
Aus dem vorherigen Lernpfad wissen wir, dass das Längenverhältnis von Strecken bei einer zentrischen Streckung, wegen der
Eigenschaft der Längenverhältnistreue, gleich ist.
Was bedeutet dies? Eine kleine Wiederholung kann nicht schaden. Setze dafür die richtige Aussage in die passende Lücke ein:


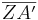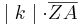
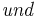
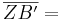
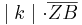
\overline{ZA'} = \mid k\mid \cdot \overline{ZA} \mathit{und}\ \overline{ZB'} = \mid k \mid \cdot \overline{ZB}
Aufgelöst nach |k|:
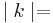
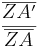
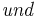
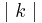
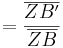
\mid k \mid = {\overline{ZA'}\over\overline{ZA}} \mathit{und}\ \mid k \mid = {\overline{ZB'}\over\overline{ZB}}
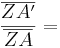
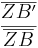
Gleichsetzen: {\overline{ZA'}\over\overline{ZA}} = {\overline{ZB'}\over\overline{ZB}}
Einsetzen der Werte ergibt:
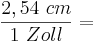
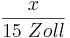
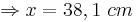
{{2,54\ cm}\over{1\ Zoll}} = {x}\over{15\ Zoll} \Rightarrow x = 38,1\ cm

 


Porzelt lobenderPanto8.jpg

Porzelt Panto-2.jpg

Die Formel sagt aus, dass sich die Abschnitte auf der einen Halbgeraden genauso verhalten wie die Abschnitte auf der anderen
Halbgeraden. Diesen Satz nennt man den ersten Vierstreckensatz. In unserem Beispiel wurden die Schenkel betrachtet,
deshalb wird es auch die Schenkellösung genannt.


\Rightarrow Weiter zur 2. Station: Erster Vierstreckensatz - Abschnittlösung
Von „http://dmuw.zum.de/index.php?title=Lernpfade/Zentrische_Streckung/Vierstreckensatz&oldid=10371“