5.Station: Unterschied zwischen den Versionen
Aus DMUW-Wiki
(Formel bearbeitet) |
K |
||
| (9 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
<div style="margin:0; margin-right:4px; margin-left:0px; border:2px solid #f4f0e4; padding: 0em 0em 0em 1em; background-color:#f4f0e4;"> | <div style="margin:0; margin-right:4px; margin-left:0px; border:2px solid #f4f0e4; padding: 0em 0em 0em 1em; background-color:#f4f0e4;"> | ||
| − | [[ | + | [[Lernpfade/Zentrische Streckung/Eigenschaften der zentrischen Streckung|1. Station: Fixelemente]] - [[Lernpfade/Zentrische Streckung/Eigenschaften der zentrischen Streckung/2.Station|2. Station: Geradentreue und Parallelentreue]] - [[Lernpfade/Zentrische Streckung/Eigenschaften der zentrischen Streckung/3.Station|3. Station: Winkeltreue, Längentreue und Flächeninhaltstreue]] - [[Lernpfade/Zentrische Streckung/Eigenschaften der zentrischen Streckung/4.Station|4. Station: Längenverhältnistreue]] - [[Lernpfade/Zentrische Streckung/Eigenschaften der zentrischen Streckung/5.Station|5. Station: Kreistreue]] - [[Lernpfade/Zentrische Streckung/Eigenschaften der zentrischen Streckung/6.Station|6. Station: Zusammenfassung]] - [[Lernpfade/Zentrische Streckung/Eigenschaften der zentrischen Streckung/7.Station|7. Station: Übung]] |
</div> | </div> | ||
<br> | <br> | ||
==5. Station: Kreistreue== | ==5. Station: Kreistreue== | ||
| + | [[Bild:Porzelt_lobenderDia4.jpg]] | ||
| + | <br> | ||
<div style="border: 2px solid #ffd700; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid #ffd700; background-color:#ffffff; padding:7px;"> | ||
[[Bild:Porzelt_Panto-2.jpg|left]] <br>'''Kreistreue''' liegt vor, wenn das Bild eines Kreises ebenfalls ein Kreis ist. | [[Bild:Porzelt_Panto-2.jpg|left]] <br>'''Kreistreue''' liegt vor, wenn das Bild eines Kreises ebenfalls ein Kreis ist. | ||
| Zeile 10: | Zeile 12: | ||
</div> | </div> | ||
<br> | <br> | ||
| − | + | '''''Mit Hilfe dieses Applets kannst du einen Kreis k zentrisch um den Faktor m = 3 strecken. (Der Streckungsfaktor wurde in'''''<br> | |
| − | + | '''''diesem Fall mit m bezeichnet, da der Kreis die Abkürzung k besitzt.)'''''<br> | |
| − | + | '''''Finde heraus, ob die zentrische Streckung kreistreu ist!'''''<br> | |
<div style="border: 2px solid #00CD00; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid #00CD00; background-color:#ffffff; padding:7px;"> | ||
| − | <ggb_applet height="350" width="650" showResetIcon="true" filename="Porzelt_Kreistreue.ggb" /> | + | {| |
| − | + | |<ggb_applet height="350" width="650" showResetIcon="true" filename="Porzelt_Kreistreue.ggb" />|| | |
| − | + | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
Es gilt: <math>\overline{PM} = r</math> <br> | Es gilt: <math>\overline{PM} = r</math> <br> | ||
| − | Deshalb kann man schreiben: <math>\overline{P'M'} =</math> '''|m|''' <math>\cdot \overline{PM} = r'</math> <br> | + | Deshalb kann man schreiben: <br> |
| − | Der Bildpunkt P' liegt auf dem '''Kreis k'''' um M' mit Radius r' = |m| ∙ '''r'''. | + | <math>\overline{P'M'} =</math> '''|m|''' <math>\cdot \overline{PM} = r'</math> <br> |
| + | Der Bildpunkt P' liegt auf dem '''Kreis k'''' um M' mit Radius <br> | ||
| + | r' = |m| ∙ '''r'''. | ||
</div> | </div> | ||
| + | |} | ||
| + | | ||
| + | </div> | ||
| + | <br> | ||
| + | [[Bild:Porzelt_lobenderDia6.jpg]] | ||
<br> | <br> | ||
| Zeile 29: | Zeile 37: | ||
</div> | </div> | ||
<br> | <br> | ||
| − | <div align=" | + | <div align="left">[[Lernpfade/Zentrische Streckung/Eigenschaften der zentrischen Streckung/6.Station|<math>\Rightarrow</math> Weiter zur 6. Station: Zusammenfassung]]</div> |
| − | <div align="left">[[ | + | <br> |
| + | <div align="left">[[Lernpfade/Zentrische Streckung/Eigenschaften der zentrischen Streckung/4.Station|<math>\Leftarrow</math> Zurück zur 4. Station: Längenverhältnistreue]]</div> | ||
Aktuelle Version vom 7. August 2009, 10:24 Uhr
1. Station: Fixelemente - 2. Station: Geradentreue und Parallelentreue - 3. Station: Winkeltreue, Längentreue und Flächeninhaltstreue - 4. Station: Längenverhältnistreue - 5. Station: Kreistreue - 6. Station: Zusammenfassung - 7. Station: Übung
5. Station: Kreistreue
Mit Hilfe dieses Applets kannst du einen Kreis k zentrisch um den Faktor m = 3 strecken. (Der Streckungsfaktor wurde in
diesem Fall mit m bezeichnet, da der Kreis die Abkürzung k besitzt.)
Finde heraus, ob die zentrische Streckung kreistreu ist!
|
Es gilt: |
Ist die zentrische Streckung kreistreu? (Ja) (!Nein)


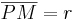
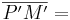 |m|
|m| 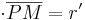

 Weiter zur 6. Station: Zusammenfassung
Weiter zur 6. Station: Zusammenfassung Zurück zur 4. Station: Längenverhältnistreue
Zurück zur 4. Station: Längenverhältnistreue
