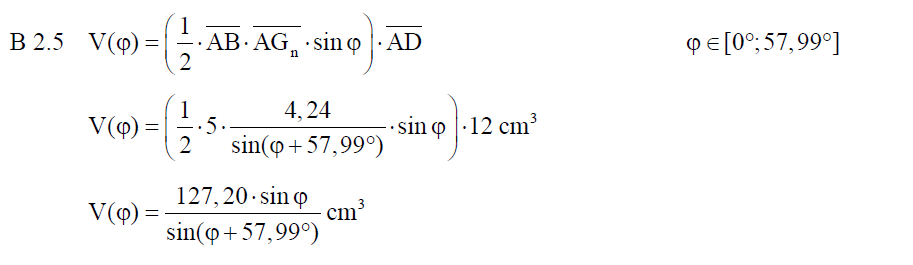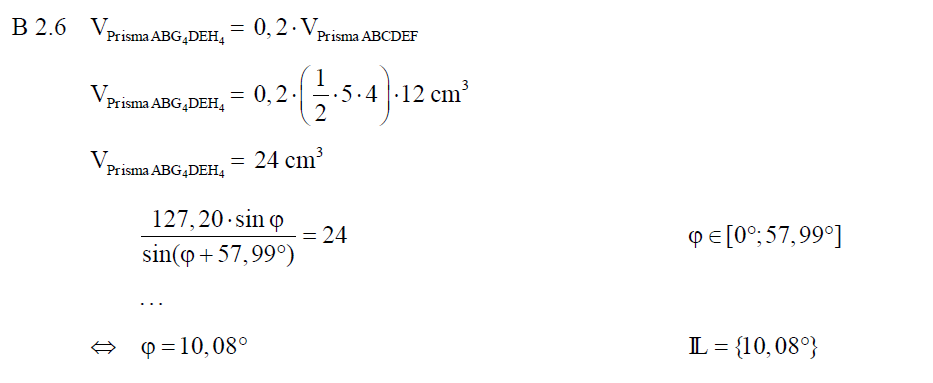Abschlussprüfung 2009B: Unterschied zwischen den Versionen
(Struktur geändert) |
|||
| (6 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | {{Vorlage:Prüfungsaufgaben}} | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
==Abschlussprüfung 2009 - Aufgabe B== | ==Abschlussprüfung 2009 - Aufgabe B== | ||
| Zeile 94: | Zeile 76: | ||
{| border="1" | {| border="1" | ||
| − | |''' | + | |'''B 1.3''' Punkte <math>\quad A_n(x|log_2(x+8)+1)</math> auf dem Graphen zu f sind zusammen mit dem Punkt <math>\quad B(0|0)</math> und den Punkten <math>\quad C_n</math> und <math>\quad D_n</math> die Eckpunkte von Quadraten <math>\quad A_nBC_nD_n</math>. |
Zeichnen Sie die Quadrate <math>\quad A_1BC_1D_1</math> für <math>\quad x=-5</math> und <math>\quad A_2BC_2D_2</math> für <math>\quad x=1</math> in das Koordinatensystem zu 1.2 ein. | Zeichnen Sie die Quadrate <math>\quad A_1BC_1D_1</math> für <math>\quad x=-5</math> und <math>\quad A_2BC_2D_2</math> für <math>\quad x=1</math> in das Koordinatensystem zu 1.2 ein. | ||
|} | |} | ||
| Zeile 152: | Zeile 134: | ||
{| border="1" | {| border="1" | ||
|'''B 1.6''' Für das Quadrat <math>\quad A_4BC_4D_4</math> gilt: Der Punkt <math>\quad D_n</math> liegt auf der Winkelhalbierenden des II. Quadranten. | |'''B 1.6''' Für das Quadrat <math>\quad A_4BC_4D_4</math> gilt: Der Punkt <math>\quad D_n</math> liegt auf der Winkelhalbierenden des II. Quadranten. | ||
| − | Ermitteln Sie rechnersich die x-Koordinate des Punktes <math>\quad A_4</math> | + | Ermitteln Sie rechnersich die x-Koordinate des Punktes <math>\quad A_4</math>. |
{| | {| | ||
|[[Bild:Peter_Fischer_Tipp.png|35px|''Mori hat einen Tipp für dich'']] | |[[Bild:Peter_Fischer_Tipp.png|35px|''Mori hat einen Tipp für dich'']] | ||
| Zeile 224: | Zeile 206: | ||
{| border="1" | {| border="1" | ||
| − | |''' | + | |'''B 2.3''' Berechnen Sie den Flächeninhalt A der Rechtecke <math>\quad AG_nH_nD</math> in Abhängigkeit von <math>\quad \varphi</math>. |
Ermitteln Sie sodann den minimalen und den maximalen Flächeninhalt mit dem jeweils zugehörigen Winkelmaß <math>\quad \varphi</math>. | Ermitteln Sie sodann den minimalen und den maximalen Flächeninhalt mit dem jeweils zugehörigen Winkelmaß <math>\quad \varphi</math>. | ||
[Teilergebnis: <math>\quad \overline{AG_n}(\varphi)=\frac{4,24}{\sin(\varphi+57,99^\circ)}cm</math>] | [Teilergebnis: <math>\quad \overline{AG_n}(\varphi)=\frac{4,24}{\sin(\varphi+57,99^\circ)}cm</math>] | ||
| Zeile 306: | Zeile 288: | ||
{| border="1" | {| border="1" | ||
|'''B 2.6''' Das Volumen des Prismas <math>\quad ABG_4DEH_4</math> beträgt 20% des Volumens des Prismas <math>\quad ABCDEF</math>. | |'''B 2.6''' Das Volumen des Prismas <math>\quad ABG_4DEH_4</math> beträgt 20% des Volumens des Prismas <math>\quad ABCDEF</math>. | ||
| − | Berechnen Sie das zugehörige Winkelmaß <math>\quad varphi</math>. | + | Berechnen Sie das zugehörige Winkelmaß <math>\quad \varphi</math>. |
<quiz display="simple"> | <quiz display="simple"> | ||
| Zeile 326: | Zeile 308: | ||
<poem> | <poem> | ||
<span style="color:#FFFFFF"><big>Leerzeile</big></span> | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
| − | '''Zurück zur Übersicht [[LERNPFAD]]''' | + | '''Zurück zur Übersicht [[../../|LERNPFAD]]''' |
<span style="color:#FFFFFF"><big>Leerzeile</big></span> | <span style="color:#FFFFFF"><big>Leerzeile</big></span> | ||
</poem> | </poem> | ||
| Zeile 333: | Zeile 315: | ||
<div style="background:#EE2C2C;text-align:center;color: #fff;font-weight:bold;font-size:125%;margin: 10px 5px 0px 0; padding: 4px 4px 4px 14px;">Abbildungen im Koordinatensystem</div> | <div style="background:#EE2C2C;text-align:center;color: #fff;font-weight:bold;font-size:125%;margin: 10px 5px 0px 0; padding: 4px 4px 4px 14px;">Abbildungen im Koordinatensystem</div> | ||
<div style="margin: 0 5px 5px 0; padding: 1em 1em 1em 1em; text-align:center; border: 1px solid :#D15FEE; background-color:#f6fcfe;"> | <div style="margin: 0 5px 5px 0; padding: 1em 1em 1em 1em; text-align:center; border: 1px solid :#D15FEE; background-color:#f6fcfe;"> | ||
| − | [[LERNPFAD]] | [[Abschlussprüfung 2009 - Aufgabe A]] | [[Abschlussprüfung 2009 - Aufgabe B | + | [[../../|LERNPFAD]] | [[../Abschlussprüfung 2009A|Abschlussprüfung 2009 - Aufgabe A]] | [[../Abschlussprüfung 2009B|Abschlussprüfung 2009 - Aufgabe B]] </div><noinclude> |
Aktuelle Version vom 15. Oktober 2011, 12:20 Uhr
Abschlussprüfung 2009 - Aufgabe B
| Aufgabe B | |
| B 1.0 |
Leerzeile
| B 1.1 Geben Sie die Definitionsmenge und Wertemenge der Funktion f sowie die Gleichung der Asymptote h an. | 
| ||
|
| |||
Leerzeile
Leerzeile
B 1.3 Punkte 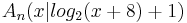 auf dem Graphen zu f sind zusammen mit dem Punkt auf dem Graphen zu f sind zusammen mit dem Punkt 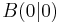 und den Punkten und den Punkten 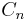 und und 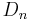 die Eckpunkte von Quadraten die Eckpunkte von Quadraten 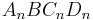 . .
Zeichnen Sie die Quadrate |
Leerzeile
B 1.4 Die Punkte 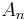 können auf die Punkte können auf die Punkte 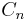 abgebildet werden. abgebildet werden.
Zeigen Sie durch Rechnung , dass der Trägergraph t der Punkte |
Leerzeile
B 1.5 Für das Quadrat 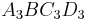 gilt: gilt: 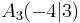 . .
Berechnen Sie die Koordinaten des Punktes
|
Leerzeile
B 1.6 Für das Quadrat 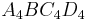 gilt: Der Punkt gilt: Der Punkt 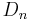 liegt auf der Winkelhalbierenden des II. Quadranten. liegt auf der Winkelhalbierenden des II. Quadranten.
Ermitteln Sie rechnersich die x-Koordinate des Punktes
|
Leerzeile
| Aufgabe B | ||
| B 2.0 |
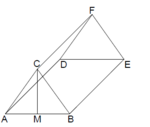
| |
Leerzeile
B 2.1 Zeichnen Sie das Schrägbild des Prismas ABCDEF, wobei die Kante ![\quad [AB]](/images/math/f/a/0/fa0ff099d7570d933396547b19b30bdb.png) auf der Schrägbildachse liegen soll (Lage des Prismas wie in der Skizze zu 2.0 dargestellt). auf der Schrägbildachse liegen soll (Lage des Prismas wie in der Skizze zu 2.0 dargestellt).
Für die Zeichnung gilt: Leerzeile |
Leerzeile
B 2.2 Die Punkte ![\quad G_n \in [BC]](/images/math/f/2/a/f2ad55997ee6374ce39452635c9d301f.png) und die Punkte und die Punkte ![\quad H_n \in [EF]](/images/math/1/5/7/157d60e7310f4e2f44c350eba279deae.png) sind zusammen mit den Punkten A und D die Eckpunkte von Rechtecken sind zusammen mit den Punkten A und D die Eckpunkte von Rechtecken 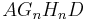 . Die Winkel BAG_n haben das Maß . Die Winkel BAG_n haben das Maß 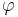 mit mit ![\quad \varphi \in [0;57,99].](/images/math/8/3/3/833e69fc189c189d9385de85d8b1cd76.png)
Zeichnen Sie das Rechteck |
Leerzeile
B 2.3 Berechnen Sie den Flächeninhalt A der Rechtecke 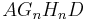 in Abhängigkeit von in Abhängigkeit von 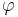 . .
Ermitteln Sie sodann den minimalen und den maximalen Flächeninhalt mit dem jeweils zugehörigen Winkelmaß
|
Leerzeile
B 2.4 Die Rechtecke 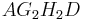 und und 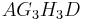 haben jeweils den Flächeninhalt 53 cm². Berechnen Sie die Zugehörigen Winkelmaße haben jeweils den Flächeninhalt 53 cm². Berechnen Sie die Zugehörigen Winkelmaße 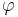 . .
|
Leerzeile
B 2.5 Ermitteln Sie rechnerisch das Volumen V der Prismen 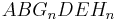 in Abhängigkeit von in Abhängigkeit von 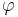 . .
[Ergebnis: Leerzeile |
Leerzeile
B 2.6 Das Volumen des Prismas 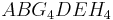 beträgt 20% des Volumens des Prismas beträgt 20% des Volumens des Prismas 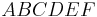 . .
Berechnen Sie das zugehörige Winkelmaß
|
Leerzeile
Zurück zur Übersicht LERNPFAD
Leerzeile
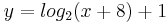 .
.
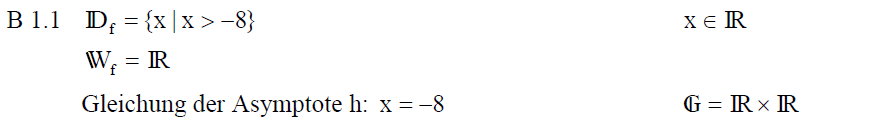
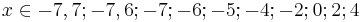 auf zwei Stellen nach dem Komma gerundet.
auf zwei Stellen nach dem Komma gerundet.
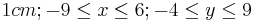


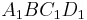 für
für 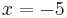 und
und 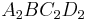 für
für 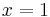 in das Koordinatensystem zu 1.2 ein.
in das Koordinatensystem zu 1.2 ein.
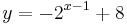 besitzt.
Zeichnen Sie den Trägergraphen t der Punkte
besitzt.
Zeichnen Sie den Trägergraphen t der Punkte 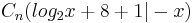 ]
]

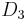 .
.

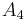 .
.
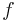 und
und 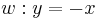 !
!

![\quad [MC]](/images/math/2/3/d/23db663786797555c592e9206a9075b4.png) ist.
ist.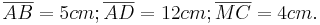 .
.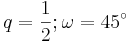 .
Brechnen Sie sodann das Maß des Winkels CBA.
[Ergebnis: Winkel
.
Brechnen Sie sodann das Maß des Winkels CBA.
[Ergebnis: Winkel 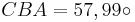 ]
]
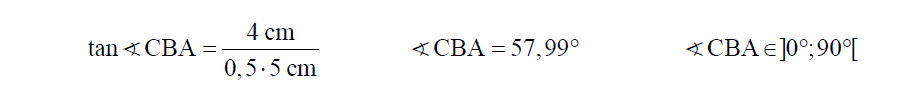
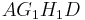 für
für 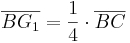 in das Schrägbild zu 2.1 ein.
in das Schrägbild zu 2.1 ein.
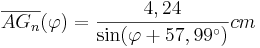 ]
]
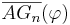 berechen und
berechen und 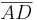 ist in allen Rechtecken gleich.
ist in allen Rechtecken gleich.
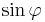 am größten/kleinsten ist.
am größten/kleinsten ist.
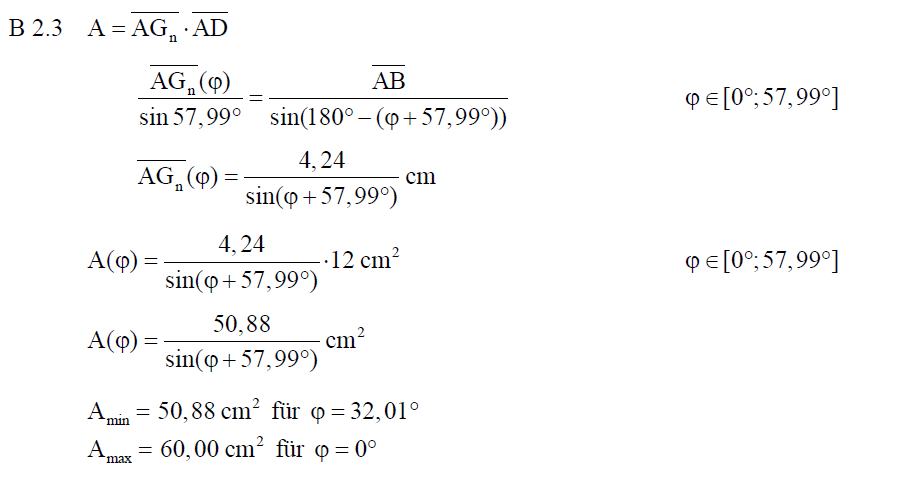
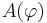 einsetzen und trigonometrische Gleichung lösen, also nach
einsetzen und trigonometrische Gleichung lösen, also nach 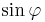 auflösen.
auflösen.
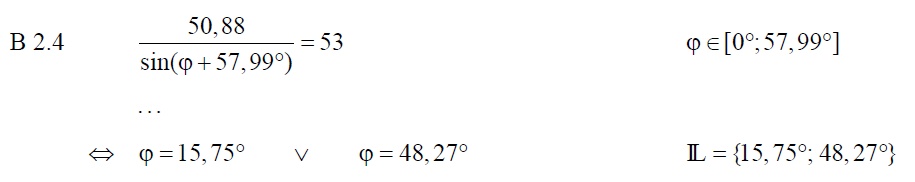
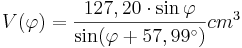 ]
]