Einen Text eingeben: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
(kat Schüler erstellen Wikis)
 
(7 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt)
Zeile 7: Zeile 7:
 
<br>schon öffnet sich ein neues Fenster.  
 
<br>schon öffnet sich ein neues Fenster.  
 
<br>
 
<br>
−
<br>[[Bild:wikifenster.jpg]]
+
<br>[[Bild:wikifenster.jpg]]<br>
−
<br>
+
 
<br>
 
<br>
 
<br>
 
<br>
Zeile 166: Zeile 165:
 
<br><span style="color: blue">'''Aufgaben'''</span>
 
<br><span style="color: blue">'''Aufgaben'''</span>
 
<br>
 
<br>
−
Setzt euch nun in den Gruppen zusammen, lest euch die Aufgabenstellungen genau durch und klickt dann auf den Namen eurer Gruppe, um die Ergebnisse ins Wiki einzugeben. Die Lösungen könnt ihr im Schulbuch der 5. Klasse, im Internet oder im besten Fall in eueren Köpfen finden. Viel Spaß!!
+
Setzt euch nun in den Gruppen zusammen, lest euch die Aufgabenstellungen genau durch und klickt dann auf den Namen eurer Gruppe, um die Ergebnisse ins Wiki einzugeben. Die Lösungen könnt ihr in den Schulbüchern der 5. und 6. Klasse, im Internet oder im besten Fall in eueren Köpfen finden. Viel Spaß!!
 
<br>
 
<br>
−
<br><span style="color: blue">[[Gruppe 1:]]</span>
+
<br><span style="color: blue">[[../Gruppe 1|Gruppe 1:]]</span> / <span style="color: blue">[[../Gruppe 6|Gruppe 6:]]</span>
 
<br>
 
<br>
 
Beschreibt das "Assoziativgesetz" (Verbindungsgesetz) und gebt an, für welche Rechenarten es gilt.
 
Beschreibt das "Assoziativgesetz" (Verbindungsgesetz) und gebt an, für welche Rechenarten es gilt.
 
<br>
 
<br>
−
<br><span style="color: green">[[Gruppe 2:]]</span>
+
<br><span style="color: green">[[../Gruppe 2|Gruppe 2:]]</span> / <span style="color: blue">[[../Gruppe 7|Gruppe 7:]]</span>
 
<br>
 
<br>
 
Beschreibt das "Kommutativgesetz" (Vertauschungsgesetz) und gebt an, für welche Rechenarten es gilt.
 
Beschreibt das "Kommutativgesetz" (Vertauschungsgesetz) und gebt an, für welche Rechenarten es gilt.
 
<br>
 
<br>
−
<br>[[Gruppe 3:]]
+
<br>[[../Gruppe 3|Gruppe 3:]] / <span style="color: blue">[[../Gruppe 8|Gruppe 8:]]</span>
 
<br>
 
<br>
 
Beschreibt das "Distributivgesetz" (Verteilungsgesetz) und gebt an, für welche Rechenarten es gilt.
 
Beschreibt das "Distributivgesetz" (Verteilungsgesetz) und gebt an, für welche Rechenarten es gilt.
 
<br>
 
<br>
−
<br><span style="color: darkblue">[[Gruppe 4:]]</span>
+
<br><span style="color: darkblue">[[../Gruppe 4|Gruppe 4:]]</span> / <span style="color: blue">[[../Gruppe 9|Gruppe 9:]]</span>
 
<br>
 
<br>
−
Gebt an, um welches Gesetz es sich handelt und gebt ein Formelbesipiel an. Für das Assoziativgesetz würde das Formelbespiel so aussehen:  a •
+
Gebt an, um welches Gesetz es sich handelt und gebt ein Formelbeispiel an. Für das Assoziativgesetz würde das Formelbeispiel so aussehen:  a •
 
b • c = (a • b) • c = a • (b • c)
 
b • c = (a • b) • c = a • (b • c)
 
<br> "Das Gesetz sagt aus, wie man in einer Rechnung, die sich aus Punkt- und Strichrechnungen zusammensetzt, "ausklammern" bzw. "ausmultiplizieren" kann."
 
<br> "Das Gesetz sagt aus, wie man in einer Rechnung, die sich aus Punkt- und Strichrechnungen zusammensetzt, "ausklammern" bzw. "ausmultiplizieren" kann."
 
<br>
 
<br>
−
<br><span style="color: brown">[[Gruppe 5:]]</span>
+
<br><span style="color: brown">[[../Gruppe 5|Gruppe 5:]]</span> / <span style="color: blue">[[../Gruppe 10|Gruppe 10:]]</span>
 
<br>
 
<br>
−
Gebt an, um welches Gesetz es sich handelt und gebt ein Formelbesipiel an. Für das Assoziativgesetz würde das Formelbespiel so aussehen:  a •
+
Gebt an, um welches Gesetz es sich handelt und gebt ein Formelbeispiel an. Für das Assoziativgesetz würde das Formelbeispiel so aussehen:  a •
 
b • c = (a • b) • c = a • (b • c)
 
b • c = (a • b) • c = a • (b • c)
 
<br> "Das Gesetz sagt aus, dass man die Summanden in einer Summe oder die Faktoren in einem Produkt vertauschen kann. Es gilt '''nicht''' für Subtraktionen und Divisionen."
 
<br> "Das Gesetz sagt aus, dass man die Summanden in einer Summe oder die Faktoren in einem Produkt vertauschen kann. Es gilt '''nicht''' für Subtraktionen und Divisionen."
Zeile 196: Zeile 195:
 
===[[../Bild|Texte ohne Bilder sind langweilig, oder?]]===
 
===[[../Bild|Texte ohne Bilder sind langweilig, oder?]]===
 
}}
 
}}
 +
 +
 +
 +
[[Kategorie:Schüler erstellen Wikis|Einen Text eingeben]]

Aktuelle Version vom 27. Dezember 2011, 23:50 Uhr

Text.jpg



... dazu musst du eigentlich nur oben auf den Button "bearbeiten" klicken,

Bearbeiten2.jpg

schon öffnet sich ein neues Fenster.

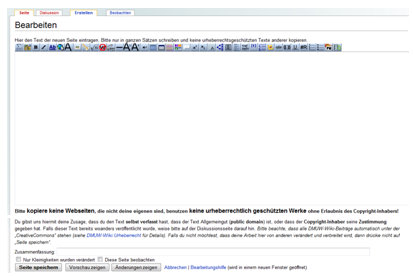
Wikifenster.jpg


In diesem Fenster kannst du deinen Text einfach eingeben, wie in einem Schreibprogramm.
Anschließend klickst du unterhalb des Eingabefeldes auf den Button "Seite speichern".


Speichern.jpg


Schon erscheint dein Text auf der ursprünglichen Seite.

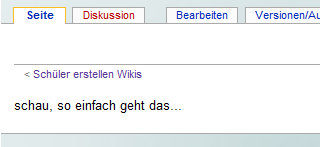
Fertig.jpg


Genauso kannst du auch einen Text, der bereits eingegeben wurde, verändern oder löschen.



Ähnlich wie in einem Schreibprogramm hast du auch hier die Möglichkeit, einen Text zu formatieren. In der folgenden Tabelle habe ich die wichtigsten Befehle für dich zusammengefasst. Du musst sie dir nicht merken, das Wiki merkt sie sich ;-). Du kannst immer wieder auf diese Seite zurückkehren und dir einen Befehl heraussuchen.

Merkesmily.jpg
Das gibst du ein und so wird es dargestellt
Normaler Text erscheint genau so, wie du ihn eingibst

Normaler Text erscheint genau so, wie du ihn eingibst
Eine Leerzeile erzeugst du durch die Eingabe von <br> schon bist du in der nächsten Zeile Eine Leerzeile erzeugst du durch die Eingabe von
schon bist du in der nächsten Zeile
''kursiv'' kursiv
'''fett''' fett
'''''fett und kursiv''''' fett und kursiv
<sup>hochgestellt</sup> Text hochgestellt
<sub>tiefgestellt</sub> Text tiefgestellt

== Überschrift Ebene 2 ==

=== Überschrift Ebene 3 ===

==== Überschrift Ebene 4 ====

===== Überschrift Ebene 5 =====

====== Überschrift Ebene 6 ======
Überschrift Ebene 2
Überschrift Ebene 3

Überschrift Ebene 4

Überschrift Ebene 5

Überschrift Ebene 6
* eins
  • zwei
    • zwei-eins
    • zwei-zwei
  • drei
  • eins
  • zwei
    • zwei-eins
    • zwei-zwei
  • drei
# eins
  1. zwei
    1. zwei-eins
    2. zwei-zwei
  1. drei
  1. eins
  2. zwei
    1. zwei-eins
    2. zwei-zwei
  3. drei
<code>Markiert Text als Quelltext</code> Markiert Text als Quelltext
Dies ist ein<!-- unsichtbarer Kommentar-->. Dies ist ein.



Das wars von meiner Seite, jetzt bist du an der Reihe. Ich habe hier etwas für dich vorbereitet.

Aufgaben
Setzt euch nun in den Gruppen zusammen, lest euch die Aufgabenstellungen genau durch und klickt dann auf den Namen eurer Gruppe, um die Ergebnisse ins Wiki einzugeben. Die Lösungen könnt ihr in den Schulbüchern der 5. und 6. Klasse, im Internet oder im besten Fall in eueren Köpfen finden. Viel Spaß!!

Gruppe 1: / Gruppe 6:
Beschreibt das "Assoziativgesetz" (Verbindungsgesetz) und gebt an, für welche Rechenarten es gilt.

Gruppe 2: / Gruppe 7:
Beschreibt das "Kommutativgesetz" (Vertauschungsgesetz) und gebt an, für welche Rechenarten es gilt.

Gruppe 3: / Gruppe 8:
Beschreibt das "Distributivgesetz" (Verteilungsgesetz) und gebt an, für welche Rechenarten es gilt.

Gruppe 4: / Gruppe 9:
Gebt an, um welches Gesetz es sich handelt und gebt ein Formelbeispiel an. Für das Assoziativgesetz würde das Formelbeispiel so aussehen: a • b • c = (a • b) • c = a • (b • c)
"Das Gesetz sagt aus, wie man in einer Rechnung, die sich aus Punkt- und Strichrechnungen zusammensetzt, "ausklammern" bzw. "ausmultiplizieren" kann."

Gruppe 5: / Gruppe 10:
Gebt an, um welches Gesetz es sich handelt und gebt ein Formelbeispiel an. Für das Assoziativgesetz würde das Formelbeispiel so aussehen: a • b • c = (a • b) • c = a • (b • c)
"Das Gesetz sagt aus, dass man die Summanden in einer Summe oder die Faktoren in einem Produkt vertauschen kann. Es gilt nicht für Subtraktionen und Divisionen."

Die erste Lektion hast du also schon erfolgreich abgehakt, auf zur nächsten:

Mathematik-digital Pfeil-3d.png
Lernpfad
Von „http://dmuw.zum.de/index.php?title=Schüler_erstellen_Wikis/Einen_Text_eingeben&oldid=30671“