Beispielaufgabe: Unterschied zwischen den Versionen
Aus DMUW-Wiki
(Die Seite wurde neu angelegt: == Beispielaufgabe: Kleeblatt-Modellierung == <br /> right <u>'''Aufgabe:'''</u> Berechne die Blattfläche eines Wiesen-Klees! <br /> '''1. Wa...) |
|||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | [[../|Zurück]]<br /> | ||
== Beispielaufgabe: Kleeblatt-Modellierung == | == Beispielaufgabe: Kleeblatt-Modellierung == | ||
<br /> | <br /> | ||
| Zeile 21: | Zeile 22: | ||
3cm <math>\cdot</math> 1,5cm = 4,5cm² | 3cm <math>\cdot</math> 1,5cm = 4,5cm² | ||
Das Rechteck hat also eine Fläche von 4,5cm². | Das Rechteck hat also eine Fläche von 4,5cm². | ||
| − | Die Blattfläche des Wiesen-Klees wäre dann wegen der drei Blätter 3 <math>\cdot</math> 4,5cm², also 13,5cm².<br /> | + | Die Blattfläche des Wiesen-Klees wäre dann wegen der drei Blätter 3 <math>\cdot</math> 4,5cm², also <span style="border: 2px solid #00cd00;">13,5cm²</span>.<br /> |
<br /> | <br /> | ||
'''5. Bin ich mit dem Ergebnis zufrieden?'''<br /> | '''5. Bin ich mit dem Ergebnis zufrieden?'''<br /> | ||
| Zeile 42: | Zeile 43: | ||
die nicht ganz ausgefüllt sind, zu vollen Quadraten zusammen (8). | die nicht ganz ausgefüllt sind, zu vollen Quadraten zusammen (8). | ||
Das sind insgesamt 69 Quadrate und ein Blatt wäre demnach 69 <math>\cdot</math> 0,05cm², also 3,45cm² groß. | Das sind insgesamt 69 Quadrate und ein Blatt wäre demnach 69 <math>\cdot</math> 0,05cm², also 3,45cm² groß. | ||
| − | Die Blattfläche des Wiesen-Klees wäre dann 3 <math>\cdot</math> 3,45cm², also 10,35cm² groß.<br /> | + | Die Blattfläche des Wiesen-Klees wäre dann 3 <math>\cdot</math> 3,45cm², also <span style="border: 2px solid #00cd00;">10,35cm²</span> groß.<br /> |
<br /> | <br /> | ||
'''8. Bin ich mit dem Ergebnis zufrieden?'''<br /> | '''8. Bin ich mit dem Ergebnis zufrieden?'''<br /> | ||
| Zeile 62: | Zeile 63: | ||
1 Quadrat entspricht 8,385cm² : 90 <math>\approx</math> 0,0932cm² | 1 Quadrat entspricht 8,385cm² : 90 <math>\approx</math> 0,0932cm² | ||
69 Quadraten entspricht 0,09cm² <math>\cdot</math> 69 = 6,21cm² | 69 Quadraten entspricht 0,09cm² <math>\cdot</math> 69 = 6,21cm² | ||
| − | Die Blattfläche des Wiesen-Klees wäre jetzt 3 <math>\cdot</math> 6,21cm², also 18,63cm².<br /> | + | Die Blattfläche des Wiesen-Klees wäre jetzt 3 <math>\cdot</math> 6,21cm², also <span style="border: 2px solid #00cd00;">18,63cm²</span>.<br /> |
<br /> | <br /> | ||
'''11. Bin ich mit dem Ergebnis zufrieden?'''<br /> | '''11. Bin ich mit dem Ergebnis zufrieden?'''<br /> | ||
Da ich jetzt meine Berechnung durch die Internetrecherche von Breite und Länge eines Kleeblatts | Da ich jetzt meine Berechnung durch die Internetrecherche von Breite und Länge eines Kleeblatts | ||
noch einmal verbessert habe, bin ich mit meinem Ergebnis zufrieden.<br /> | noch einmal verbessert habe, bin ich mit meinem Ergebnis zufrieden.<br /> | ||
Aktuelle Version vom 21. September 2010, 12:15 Uhr
Beispielaufgabe: Kleeblatt-Modellierung
Aufgabe: Berechne die Blattfläche eines Wiesen-Klees!
1. Was ist gegeben?
Auf dem Bild sind drei Blätter zu sehen.
2. Welche Angaben muss ich noch heraussuchen?
Ich muss jetzt noch herausfinden, wie breit und wie lang ein Blatt ist.
3. Wie habe ich die fehlenden Größen herausgefunden?
Ich schätze jetzt erst einmal die Länge eines Blattes auf 3cm und die Breite auf 1,5cm.
4. Berechnung
Ich berechne zunächst einmal das Rechteck mit der Länge 3cm und der Breite 1,5cm,
da es von der Form her so ähnlich ist wie ein Kleeblatt.
3cm 
1,5cm = 4,5cm²
Das Rechteck hat also eine Fläche von 4,5cm².
Die Blattfläche des Wiesen-Klees wäre dann wegen der drei Blätter 3 4,5cm², also 13,5cm².
5. Bin ich mit dem Ergebnis zufrieden?
Ich bin mit dem Ergebnis noch nicht zufrieden,
da das Kleeblatt ja nicht ganz die Form eines Rechtecks hat.
Die Fläche von 13,5cm² ist also zu groß.
6. Bessere Methode
Um die Fläche des Kleeblatts besser berechnen zu können,
teile ich das Rechteck in Quadrate ein.
7. Bessere Berechnung
Auf dem Bild kann ich nun abzählen, dass der Breite des Rechtecks 10 Quadrate
und der Länge 9 Quadrate entsprechen.
Jetzt kann ich ausrechnen, wie groß ein Quadrat ist:
90 Quadraten entspricht 4,5cm²
1 Quadrat entspricht 4,5cm² : 90 = 0,05cm²
Dann zähle ich im Bild vollen Quadrate (61) und füge die Quadrate,
die nicht ganz ausgefüllt sind, zu vollen Quadraten zusammen (8).
Das sind insgesamt 69 Quadrate und ein Blatt wäre demnach 69 0,05cm², also 3,45cm² groß.
Die Blattfläche des Wiesen-Klees wäre dann 3 3,45cm², also 10,35cm² groß.
8. Bin ich mit dem Ergebnis zufrieden?
Ich bin noch nicht ganz mit dem Ergebnis zufrieden,
da ich die Länge und die Breite des Kleeblatts bisher nur geschätzt habe.
9. Bessere Methode
Eine Recherche im Internet auf Wikipedia ergibt:
Länge eines Kleeblatts: 18 - 60mm
Breite eines Kleeblatts: 8 - 35mm
10. Bessere Berechnung
Nun kann ich von der Länge und der Breite des Kleeblatts den Mittelwert bilden:
Mittelwert der Länge: (18mm + 60mm) : 2 = 3,9cm
Mittelwert der Breite: (8mm + 35mm) : 2 = 2,15cm
Um die Größe der Quadrate berechnen zu können,
muss ich nun erst einmal das Rechteck mit den neuen Größen berechnen:
3,9cm 2,15cm = 8,385cm²
1 Quadrat entspricht 8,385cm² : 90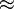 
0,0932cm²
69 Quadraten entspricht 0,09cm² 69 = 6,21cm²
Die Blattfläche des Wiesen-Klees wäre jetzt 3 6,21cm², also 18,63cm².
11. Bin ich mit dem Ergebnis zufrieden?
Da ich jetzt meine Berechnung durch die Internetrecherche von Breite und Länge eines Kleeblatts
noch einmal verbessert habe, bin ich mit meinem Ergebnis zufrieden.
