9 Gruppe06: Unterschied zwischen den Versionen
Aus DMUW-Wiki
(→Mathematik benutzen) |
(→Ergebnis erklären) |
||
| (2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 17: | Zeile 17: | ||
1 Rechteck <math>\widehat{=}</math> 3 Matratzen + Gang <br> | 1 Rechteck <math>\widehat{=}</math> 3 Matratzen + Gang <br> | ||
20m:2,5m=8 Rechtecke <br> | 20m:2,5m=8 Rechtecke <br> | ||
| − | 10m:3,5m=2,87 <math>\approx</math> 2 Rechtecke | + | 10m:3,5m=2,87 <math>\approx</math> 2 Rechtecke <br> |
| + | 8 Rechtecke<math> \cdot</math>2 Rechtecke=16 Rechtecke <br> | ||
| + | 16 Rechtecke<math> \cdot</math>3 Matratzen=<span style="background:purple">48 Matratzen</span> | ||
===<u>Ergebnis erklären</u>=== | ===<u>Ergebnis erklären</u>=== | ||
| − | + | Wir haben den Flächeninhalt der Turnhalle und einer Matratze berechnet. Danach haben wir ein Rechteck bestehend aus 3 Matratzen + Gang berechnet und dann ausgerechnet, wie viele Matratzen in die Turnhalle passen. | |
<br> | <br> | ||
<br> | <br> | ||
Aktuelle Version vom 20. Oktober 2010, 08:15 Uhr
Lösung der Hochwasseraufgabe Gruppe06
Aufgabe
In Deutschland müssen wegen Hochwasser immer wieder Dörfer und Städte evakuiert werden. Die Bewohner werden hierfür in Notunterkünften untergebracht. Als solche Notunterkünfte dienen zum Beispiel Turnhallen. Wie viele Menschen glaubst du können in einer Turnhalle auf Matratzenlagern untergebracht werden?
Aufgabe verstehen
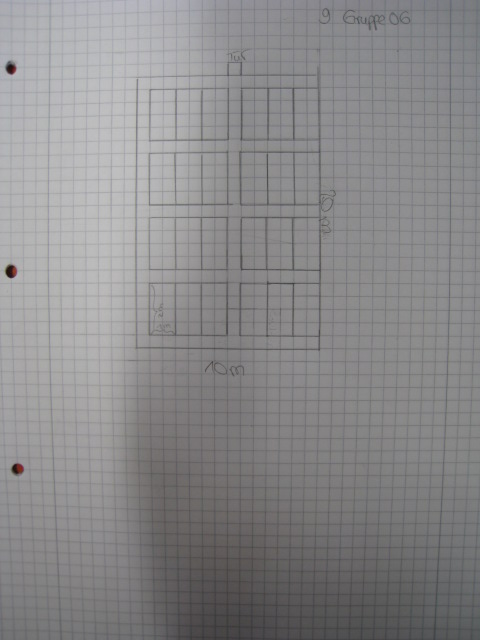
Die Turnhalle ist 20m lang und 10m breit. Eine Matratze ist 1m lang und 2m breit. Außerdem benötigt man noch Gänge zwischen den Matratzen. Ein Gang ist 50cm breit.
Modell erstellen
Mathematik benutzen
ATurnhalle=20m
10m=200m2
AMatratze=1m2m=2m2
1 Rechteck 
3 Matratzen + Gang
20m:2,5m=8 Rechtecke
10m:3,5m=2,87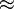 
2 Rechtecke
8 Rechtecke2 Rechtecke=16 Rechtecke
16 Rechtecke3 Matratzen=48 Matratzen
Ergebnis erklären
Wir haben den Flächeninhalt der Turnhalle und einer Matratze berechnet. Danach haben wir ein Rechteck bestehend aus 3 Matratzen + Gang berechnet und dann ausgerechnet, wie viele Matratzen in die Turnhalle passen.
