Grundlagen der Zerlegungsgleichheit von Figuren: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
(→‎Wiederholung des Kongruenzbegriffes)
(Fehler ausgebessert)
 
(79 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
−
Auf dieser Seite lernst Du die Eigenschaften der Zerlegungsgleichheit von Figuren kennen.
+
__NOTOC__
  
−
==Grundlagen der Zerlegungsgleichheit von Figuren==
+
 
−
===Wiederholung des Kongruenzbegriffes===
+
== Grundlagen der Zerlegungsgleichheit von Figuren==
−
----
+
'''''Auf dieser Seite lernst Du die Eigenschaften der Zerlegungsgleichheit von Figuren kennen.'''''
 +
 
 +
'''''Bearbeite die Aufgaben sorgfältig!''''' <br>
 +
'''''Nicht mogeln...schaue erst die Lösungen an, wenn du die Aufgaben selbstsändig bearbeitet hast!'''''
 +
'''''Denn nur so lernst du am Besten!'''''
 
<br>
 
<br>
−
Weißt Du noch was man unter '''Kongruenz von Figuren''' versteht??
 
  
−
Eine Wiederholung kann nicht schaden, oder?
+
=== Wiederholung des Kongruenzbegriffes===
 +
[[Bild:Ebert_MotivatorKongruenz.jpg|center]]
 +
 
 +
<br>
 +
:'''''Weißt Du noch was man unter '<span style="color: green">'''''Kongruenz von Figuren'''''</span> '''versteht??'''''
 +
 
 +
:'''''Eine Wiederholung kann sicher nicht schaden.'''''
 +
 
 +
=== Teste Dein Wissen!===
  
−
===Los geht´s: Teste Dein Wissen!===
 
−
----
 
 
<br>
 
<br>
 
<div class="schuettel-quiz">
 
<div class="schuettel-quiz">
−
Ein anderes Wort für Kongruenz ist '''Deckungsgleichheit'''
+
:Ein anderes Wort für Kongruenz ist '''Deckungs'''-gleichheit
 
</div>
 
</div>
 
<br>
 
<br>
 +
:'''Hinweis''': <span style="color:#008B00 ">'''Kongruente'''</span> Figuren kann man zur <span style="color:#008B00 ">'''Deckung'''</span> bringen
 +
 +
 +
  
−
===Aufgabe: Wie erzeugt man kongruente Figuren?===
 
−
<br>
 
 
===Aufgabe: Kongruente Dreiecke===
 
===Aufgabe: Kongruente Dreiecke===
 
<br>
 
<br>
−
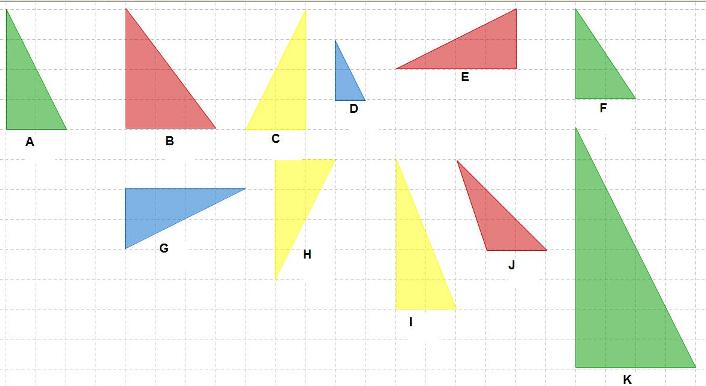
Findest Du alle Dreiecke, die zum Dreieck A kongruent sind?<br>Gib die Buchstaben an und begründe warum.
+
:'''''Findest Du alle Dreiecke, die zum <span style="color: green">Dreieck A</span> kongruent sind?'''''<br>'''''''Gib die Buchstaben an.'''''''
 
<br>
 
<br>
−
Lösung:<br>
+
[[Bild:Ebert_imageKongruenteDreiecke.jpg|center]]
−
Kongruente Dreiecke zu A sind: <u style="color:lightgrey;background:lightgrey">E,F (Drehung); C(Spiegelung);G(Drehung und Spiegelung)</u>
+
 
<br>
 
<br>
−
Welche Dreiecke sind ähnlich zu A??<br>
 
−
Antwort:<u style="color:lightgrey;background:lightgrey">C,D,E,F,G,J</u> sind ähnlich zu A
 
−
<br>
 
−
===Kleines Quiz===
 
−
Achtung!! Mehrere Antworten sind möglich!
 
 
<quiz display="simple">
 
<quiz display="simple">
−
{ Markiere die richtigen Antworten}
+
{'''Kongruente Dreiecke zu A sind?'''}  
−
- alle zueinander ähnlichen Figuren sind kongurent zueinander
+
-'''<span style="color: red">B</span> und <span style="color: blue">D</span>'''
−
+ alle zueinander kongruenten Figuren sind ähnlich zueinander
+
+'''<span style="color: gold">C</span> und <span style="color: red">E</span>'''
−
- alle kongruenten Figuren haben die gleiche Farbe
+
+'''<span style="color: blue">G</span> und <span style="gold: gold">H</span>'''
−
+ alle kongruenten Figuren haben den gleichen Flächeninhalt
+
-'''<span style="color: red">J</span> und <span style="color: green">K</span>'''
 +
-'''<span style="color: gold">I</span> und <span style="color: green">F</span>'''
 +
 
 +
{ '''Markiere die richtigen Antwort'''}
 +
- alle '''kongruenten''' Figuren haben die '''gleiche Farbe'''
 +
+ alle '''kongruenten''' Figuren haben den '''gleichen Flächeninhalt'''
 +
 
 +
 
 
</quiz>
 
</quiz>
 
<br>
 
<br>
−
===Das sollest du also wissen===
+
''0-1 Punkt: Versuche die Aufgabe noch einmal.'' <br>
−
<div style="border: 2px  solid green; background-color:#ffffff; padding:7px;">
+
''2 Punkte: Sehr gut gemacht!''
 +
<br>
 +
:'''''War Deine Lösung richtig?''''' <br>
 +
 
 +
[[Bild:Ebert_Loballgemein.jpg|200px]]
 +
 
 +
 
 +
 
 +
=== Wie erzeugt man kongruente Figuren?===
 +
 
 +
<div style="border: 2px  solid blue; background-color:#ffffff; padding:7px;">
 
{|
 
{|
−
| <div class="schuettel-quiz"> <br> Zwei Figuren sind zueinander kongruent, wenn sie durch '''Verschiebung''','''Drehung''' oder '''Spiegelung'''<br> ineinander überführt werden können. <br> Diese drei Abbildungen nennt man daher auch '''Kongruenz'''-abbildungen.<br>
+
*'''''Dreieck A, B, C und D sind kongruent zueinander.'''''
−
|</div>
+
*'' '''Wie kann man die Dreiecke B, C und D ausgehend vom Dreieck A erzeugen?'''''
 +
 
 +
|<ggb_applet height="600" width="750" showResetIcon="true" filename="Ebert_Kongruenz.ggb"/>||
 +
* In der <span style="color: blue">'''1. Möglichkeit'''</span> wird das Dreieck an einer Achse '''gespiegelt'''. '''Die <span style="color: red">Spiegelachse</span> kannst Du an den <span style="color: red">roten Punkten</span> ändern. '''
 +
<br>
 +
* In der <span style="color: #00868B  ">'''2. Möglichkeit'''</span> kannst Du das Dreieck '''verschieben'''
 +
<br>
 +
* In der <span style="color: purple">'''3. Möglichkeit'''</span> kannst Du das Dreieck  '''drehen.''' Der Winkel zeigt Dir dabei an, um wieviel Grad Du das Dreieck drehst.<br>
 +
<br>
 +
|-
 +
|
 +
* ''''''<span style="color: blue">Spiegelungen, Drehungen und Verschiebungen</span>''' nennt man '''<span style="color: blue">Kongruenzabbildungen</span>'''. Dabei kann man das Dreieck A auf die Dreiecke B, C und C abbilden.''''''' <br>
 +
<br>
 +
* '''Dreieck A nennt man <span style="color: blue">Ausgangsfigur</span>, Dreieck B,C und D <span style="color: blue">Bildfiguren</span>.'''
 +
* '''Bildfigur und Ausgangsfigur sind kongruent zueinander'''
 
|}
 
|}
 
</div>
 
</div>
−
==Zerlegungsgleichheit von Figuren==
 
 
<br>
 
<br>
 
<br>
 
<br>
 
<br>
 
<br>
 
<br>
 
<br>
−
''Logbucheintrag''
+
 
−
:Übertrage folgende Definition in Dein Heft:
+
=== Das sollest Du also wissen===
−
<div style="border: 2px solid red; background-color:#ffffff; padding:7px;">
+
<div style="border: 2px solid green; background-color:#ffffff; padding:7px;">
−
{|  
+
{|
−
'''Merke''': <span style="color:#ff0000">Zerlegungsgleichheit von Figuren</span>
+
'''''Maja hat die Eigenschaften von kongruenten Figuren aufgeschrieben. Doch ein Sturm hat manche Wörter durcheinander gebracht.'''''<br> '''''Kannst Du sie wieder ordnen?'''''
−
|Zwei Figuren sind <span style="color:#ff0000">'''zerlegungsgleich,'''</span> wenn sie in paarweise <span style="color:#ff0000">'''kongruente Teilfiguren'''</span> zerlegt werden können.<br> Beispiel:
+
|[[Bild:Ebert_MotivatorHinweis.jpg|center]]||
−
<br> {{ggb|Merkbilder.ggb|Definition}}
+
<div class="schuettel-quiz">
−
<br> Figur A und Figur B sind zerlegungsgleich. Zerlegungsgleiche Figuren besitzen den gleichen <span style="color:#ff0000">'''Flächeninhalt'''</span>
+
*Zwei Figuren sind zueinander kongruent, wenn sie durch '''Verschiebung''','''Drehung''' oder '''Spiegelung'''<br> ineinander überführt werden können. <br>  
 +
*Diese drei Abbildungen nennt man daher auch '''Kongruenz'''-abbildungen.  
 +
*Kongruente Figuren haben den '''gleichen''' Flächeninhalt.<br>
 +
|</div>
 
|}
 
|}
 
</div>
 
</div>
 +
<br>
 +
<br>
 +
<br>
 +
=== Anwendung der Kongruenz===
 +
<br>
 +
:'''''Wenn zwei Dreiecke kongruent sind, dann gibt es einen Kongruenzsatz dazu. Manchmal stimmen Seiten oder Winkelgrößen überein.'''''
 +
:'''''Erinnerst Du dich noch, wie alle Sätze heißen?'''''
 +
 +
 +
<ggb_applet height="400"  width="550" showResetIcon="true" filename="Ebert_Sätze.ggb"/>
 +
Dreieck ABC und Dreieck DEF sind kongruent.
 +
 +
<div class="lueckentext-quiz">
 +
Zwei Dreiecke, die in ihren drei Seitenlängen übereinstimmen, sind kongruent: '''SSS-Satz'''<br>
 +
Zwei Dreiecke, die in einer Seitenlänge und in den dieser Seite anliegenden Winkeln übereinstimmen, sind kongruent: '''WSW-Satz'''<br>
 +
Zwei Dreiecke, die in zwei Seitenlängen und in dem eingeschlossenen Winkel übereinstimmen, sind kongruent:''' SWS-Satz'''<br>
 +
Zwei Dreiecke, die in zwei Seitenlängen und in jenem Winkel übereinstimmen, der der längeren Seite gegenüberliegt, sind kongruent: '''SsW-Satz'''
 +
</div>
 +
<br>
 +
 +
----
 +
 +
[[Bild:Ebert_Maja.jpg|250px|center]]
 +
<br>
 +
::::'''''Prima! Das war schon die erste Seite des Lernpfads. Das ging ja fix.''''<br>
 +
::::'''''Im dem nächsten Abschnitt lernst Du ein weiteres Anwendungsbeispiel für die Kongruenz kennen'''''<br>
 +
::::'''''Hier geht es weiter:'''''
 +
→[[Zerlegungsgleichheit von Figuren]]

Aktuelle Version vom 28. September 2010, 17:39 Uhr


Grundlagen der Zerlegungsgleichheit von Figuren

Auf dieser Seite lernst Du die Eigenschaften der Zerlegungsgleichheit von Figuren kennen.

Bearbeite die Aufgaben sorgfältig!
Nicht mogeln...schaue erst die Lösungen an, wenn du die Aufgaben selbstsändig bearbeitet hast! Denn nur so lernst du am Besten!

Wiederholung des Kongruenzbegriffes

Ebert MotivatorKongruenz.jpg


Weißt Du noch was man unter 'Kongruenz von Figuren versteht??
Eine Wiederholung kann sicher nicht schaden.

Teste Dein Wissen!


Ein anderes Wort für Kongruenz ist Deckungs-gleichheit


Hinweis: Kongruente Figuren kann man zur Deckung bringen



Aufgabe: Kongruente Dreiecke


Findest Du alle Dreiecke, die zum Dreieck A kongruent sind?
''Gib die Buchstaben an.''


Ebert imageKongruenteDreiecke.jpg


1. Kongruente Dreiecke zu A sind?

B und D
C und E
G und H
J und K
I und F

2. Markiere die richtigen Antwort

alle kongruenten Figuren haben die gleiche Farbe
alle kongruenten Figuren haben den gleichen Flächeninhalt

Punkte: 0 / 0


0-1 Punkt: Versuche die Aufgabe noch einmal.
2 Punkte: Sehr gut gemacht!

War Deine Lösung richtig?

Ebert Loballgemein.jpg


Wie erzeugt man kongruente Figuren?

  • Dreieck A, B, C und D sind kongruent zueinander.
  • Wie kann man die Dreiecke B, C und D ausgehend vom Dreieck A erzeugen?
  • In der 1. Möglichkeit wird das Dreieck an einer Achse gespiegelt. Die Spiegelachse kannst Du an den roten Punkten ändern.


  • In der 2. Möglichkeit kannst Du das Dreieck verschieben


  • In der 3. Möglichkeit kannst Du das Dreieck drehen. Der Winkel zeigt Dir dabei an, um wieviel Grad Du das Dreieck drehst.


  • 'Spiegelungen, Drehungen und Verschiebungen nennt man Kongruenzabbildungen. Dabei kann man das Dreieck A auf die Dreiecke B, C und C abbilden.''


  • Dreieck A nennt man Ausgangsfigur, Dreieck B,C und D Bildfiguren.
  • Bildfigur und Ausgangsfigur sind kongruent zueinander





Das sollest Du also wissen

Maja hat die Eigenschaften von kongruenten Figuren aufgeschrieben. Doch ein Sturm hat manche Wörter durcheinander gebracht.
Kannst Du sie wieder ordnen?
Ebert MotivatorHinweis.jpg
  • Zwei Figuren sind zueinander kongruent, wenn sie durch Verschiebung,Drehung oder Spiegelung
    ineinander überführt werden können.
  • Diese drei Abbildungen nennt man daher auch Kongruenz-abbildungen.
  • Kongruente Figuren haben den gleichen Flächeninhalt.




Anwendung der Kongruenz


Wenn zwei Dreiecke kongruent sind, dann gibt es einen Kongruenzsatz dazu. Manchmal stimmen Seiten oder Winkelgrößen überein.
Erinnerst Du dich noch, wie alle Sätze heißen?


Dreieck ABC und Dreieck DEF sind kongruent.

Zwei Dreiecke, die in ihren drei Seitenlängen übereinstimmen, sind kongruent: SSS-Satz
Zwei Dreiecke, die in einer Seitenlänge und in den dieser Seite anliegenden Winkeln übereinstimmen, sind kongruent: WSW-Satz
Zwei Dreiecke, die in zwei Seitenlängen und in dem eingeschlossenen Winkel übereinstimmen, sind kongruent: SWS-Satz
Zwei Dreiecke, die in zwei Seitenlängen und in jenem Winkel übereinstimmen, der der längeren Seite gegenüberliegt, sind kongruent: SsW-Satz


Ebert Maja.jpg


Prima! Das war schon die erste Seite des Lernpfads. Das ging ja fix.'
Im dem nächsten Abschnitt lernst Du ein weiteres Anwendungsbeispiel für die Kongruenz kennen
Hier geht es weiter:

→Zerlegungsgleichheit von Figuren

Von „http://dmuw.zum.de/index.php?title=Lernpfade/Flächeninhalt_ebener_Figuren/Grundlagen_der_Zerlegungsgleichheit_von_Figuren&oldid=27213“