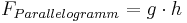Die Flächeninhaltsformel des Parallelogramms: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
K (Link eingefügt)
(Seite verschoben)
 
(Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt)
Zeile 12: Zeile 12:
 
  |[[Bild:Ebert_MotivatorHinweis.jpg|200px]] || [[Bild:Ebert_MerkbildParallelogrammneu.jpg|center]]
 
  |[[Bild:Ebert_MotivatorHinweis.jpg|200px]] || [[Bild:Ebert_MerkbildParallelogrammneu.jpg|center]]
 
<div class="lueckentext-quiz">
 
<div class="lueckentext-quiz">
−
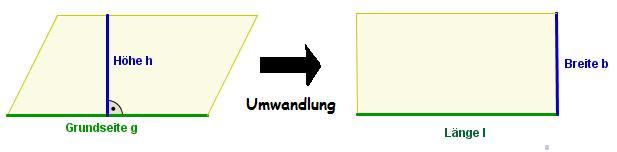
*Länge   l('''Rechteck''') = '''Grundseite g'''(Parallelogramm)<br>
+
*Länge l ( im '''Rechteck''') entspricht  der '''Grundseite g'''( des Parallelogramms)<br>
−
Breite  b (Rechteck)    ='''Höhe h '''(Parallelogramm)<br>
+
Breite  b ( im Rechteck)    entspricht  der '''Höhe h '''( des Parallelogramms)<br>
 
*Der Flächeninhalt des Parallelogramms ist definiert als: <br>
 
*Der Flächeninhalt des Parallelogramms ist definiert als: <br>
 
F<sub>Parallelogramm</sub> = '''g''' <math>\cdot </math> h  mit <br>
 
F<sub>Parallelogramm</sub> = '''g''' <math>\cdot </math> h  mit <br>
Zeile 20: Zeile 20:
 
|}
 
|}
 
</div>
 
</div>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 
<br>
 
<br>
 
<br>
 
<br>
Zeile 37: Zeile 45:
 
</div>
 
</div>
 
<br>
 
<br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
[[Bild:Ebert_MotivatorGrün.jpg|100px|right]]
 +
'''''Stimmt denn die Flächeninhaltsformel auch bei schiefen Parallelogrammen? '''''
  
 +
 +
=== "Schiefe Parallelogramme"===
 +
 +
 +
<br>
 +
<div style="border: 2px solid blue; background-color:#ffffff; padding:7px;">
 +
{|
 +
|<ggb_applet height="400" width="600" showResetIcon="true" filename="Ebert_Parallelogramm2.ggb"/>|| '''Aufgabenstellung:'''
 +
'''1.''' '''Verschiebe das <span style="color: green">dunkel-grüne</span> Dreieck'''
 +
<quiz display="simple">
 +
 +
{ '''Welche Figur ensteht?'''}
 +
-Trapez
 +
+Rechteck
 +
-Sechseck
 +
-Quadrat
 +
 +
</quiz>
 +
 +
 +
'''2.''' Erkläre, welche '''Idee''' hinter dieser Zerlegung des Parallelogramms steckt.<br>
 +
'''Tipp:''' {{versteckt| Zeige dafür wieder die Höhe und die Grundseite an. }}
 +
<br>
 +
'''''Maja hat eine Idee gefunden. Du auch?
 +
[[Bild:Ebert_MotivatorHinweis.jpg|100px|right]]
 +
Vergleiche Deine Idee mit der von Maja:'''''<br>
 +
{{ versteckt|'''Hier werden nicht die Parallelogrammseiten betrachtet, die auf den parallelen Geraden liegen, sondern ''das andere Seitenpaar''. Entsprechend wird die ''dazugehörige Höhe'' gewählt!'''}}
 +
<br>
 +
|}
 +
</div>
 +
<br>
 +
<br>
 +
'''''Nils will dazu noch etwas sagen:'''''
 +
 +
<div style="border: 2px solid red; background-color:#ffffff; padding:7px;">
 +
{|
 +
|[[Bild:Ebert_MotivatorMerke.jpg|100px]]||
 +
Zur Berechnung des Flächeninhaltes von Parallelogrammen kann <span style="color: red">'''jede Seite''' des Parallelogrammes als Grundseite </span> und die <span style="color: red">'''zugehörige Höhe'''</span> genommen werden.<br>
 +
|}
 +
</div>
 +
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
----
 
----
 
----
 
[[Bild:Ebert_Motivatoren.jpg|200px|center]]
 
[[Bild:Ebert_Motivatoren.jpg|200px|center]]

Aktuelle Version vom 19. August 2009, 10:14 Uhr


Jetzt besitzt Du alle Grundlagen, um die Formel für die Berechnung des Flächeninhalts zu erarbeiten.
Fülle zunächst die Lücken aus und übertrage anschließend den Merkkasten in Dein Heft!


Erinnerst Du Dich noch an die Herleitungsidee?
Ebert MotivatorHinweis.jpg
Ebert MerkbildParallelogrammneu.jpg
  • Länge l ( im Rechteck) entspricht der Grundseite g( des Parallelogramms)

Breite b ( im Rechteck) entspricht der Höhe h ( des Parallelogramms)

  • Der Flächeninhalt des Parallelogramms ist definiert als:

FParallelogramm = g \cdot h mit
g als Grundseite und h als dazugehörigen Höhe











Zusammenfassung:Flächeninhaltsformel Parallelogramm


Merke Dir sehr gut, wie man den Flächeninhalt von Parallelogrammen berechnet. Du wirst später darüber abgefragt!


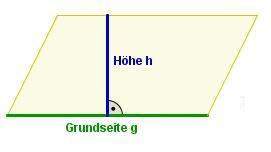
Ebert MotivatorMerke.jpg Den Flächeninhalt eines Parallelogramms berechnet man durch:
F_{Parallelogramm} = g \cdot h

g ist die Länge der Grundseite und h die Länge der dazugehörigen Höhe.

Ebert Bild3.jpg










Ebert MotivatorGrün.jpg

Stimmt denn die Flächeninhaltsformel auch bei schiefen Parallelogrammen?


"Schiefe Parallelogramme"


 Aufgabenstellung:

1. Verschiebe das dunkel-grüne Dreieck

1. { Welche Figur ensteht?

Trapez
Rechteck
Sechseck
Quadrat

Punkte: 0 / 0


2. Erkläre, welche Idee hinter dieser Zerlegung des Parallelogramms steckt.
Tipp:

Zeige dafür wieder die Höhe und die Grundseite an.


Maja hat eine Idee gefunden. Du auch?

Ebert MotivatorHinweis.jpg

Vergleiche Deine Idee mit der von Maja:

Hier werden nicht die Parallelogrammseiten betrachtet, die auf den parallelen Geraden liegen, sondern das andere Seitenpaar. Entsprechend wird die dazugehörige Höhe gewählt!




Nils will dazu noch etwas sagen:

Ebert MotivatorMerke.jpg

Zur Berechnung des Flächeninhaltes von Parallelogrammen kann jede Seite des Parallelogrammes als Grundseite und die zugehörige Höhe genommen werden.





Ebert Motivatoren.jpg

Du hast den ersten Lernpfad bald geschafft!
Nur noch ein paar Übungen.

Hier kannst Du Dein wissen testen!!

→Übung zum Flächeninhalt Parallelogramm

Hier geht es zurück zur Seite Höhen im Parallelogramm

Von „http://dmuw.zum.de/index.php?title=Die_Flächeninhaltsformel_des_Parallelogramms&oldid=4485“