Volumen des Zylinders: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
 
(5 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt)
Zeile 7: Zeile 7:
 
Nun benötigen wir aber noch die '''Grundfläche''' G. Diese besteht bei unserem Zylinder aus einem '''Kreis'''. Der '''Flächeninhalt''' des Kreises lässt sich mit '''<math>A=r^2\cdot \pi</math>''' darstellen.  
 
Nun benötigen wir aber noch die '''Grundfläche''' G. Diese besteht bei unserem Zylinder aus einem '''Kreis'''. Der '''Flächeninhalt''' des Kreises lässt sich mit '''<math>A=r^2\cdot \pi</math>''' darstellen.  
 
Also können wir die Formel für das '''Zylindervolumen''' zusammenfügen: <math>V=G\cdot h_K=r^2\cdot \pi\cdot h_K</math>.
 
Also können wir die Formel für das '''Zylindervolumen''' zusammenfügen: <math>V=G\cdot h_K=r^2\cdot \pi\cdot h_K</math>.
−
</div>
+
</div>&nbsp;
−
<br>
+
−
<br>
+
−
<br>
+
−
<br>
+
−
<br>
+
−
<br>
+
−
<br>
+
−
<br>
+
−
<br>
+
 
</div>
 
</div>
 
<br>
 
<br>
Zeile 27: Zeile 18:
 
! Schritt 1 !!  
 
! Schritt 1 !!  
 
|-
 
|-
−
| || |Als erstes lässt du ca. 10cm Platz und zeichnest dann eine waagrechte Linie mit der Länge 2r also 6cm.  
+
| [[Bild:Schritt_1.JPG|300px]]|| |Als erstes lässt du ca. 10cm Platz und zeichnest dann eine waagrechte Linie mit der Länge 2r also 6cm.  
 
|  
 
|  
 
|}
 
|}
Zeile 35: Zeile 26:
 
! Schritt 2 !!  
 
! Schritt 2 !!  
 
|-
 
|-
−
| || |Nun zeichnest du eine senkrechte Linie im Mittelpunkt der ersten Linie mit je 1,5cm Länge (nach oben und unten).
+
| [[Bild:Schritt_2.JPG|300px]]|| |Nun zeichnest du eine senkrechte Linie im Mittelpunkt der ersten Linie mit je 1,5cm Länge (nach oben und unten).
 
|  
 
|  
 
|}
 
|}
Zeile 43: Zeile 34:
 
! Schritt 3 !!  
 
! Schritt 3 !!  
 
|-
 
|-
−
| || |Als nächstes verbindest du die vier Eckpunkte zu einem schrägen Kreis bzw. zu einer Ellipse.  
+
| [[Bild:Schritt_3.JPG|300px]]|| |Als nächstes verbindest du die vier Eckpunkte zu einem schrägen Kreis bzw. zu einer Ellipse.  
 
|  
 
|  
 
|}
 
|}
Zeile 51: Zeile 42:
 
! Schritt 4 !!  
 
! Schritt 4 !!  
 
|-
 
|-
−
| || |Jetzt trägst du an den zwei Eckpunkten rechts und links jeweils die Höhe des Zylinders (7cm) senkrecht an und verbindest die Enden.
+
| [[Bild:Schritt_4.JPG|300px]]|| |Jetzt trägst du an den zwei Eckpunkten rechts und links jeweils die Höhe des Zylinders (7cm) senkrecht an und verbindest die Enden.
 
|  
 
|  
 
|}
 
|}
Zeile 59: Zeile 50:
 
! Schritt 5 !!  
 
! Schritt 5 !!  
 
|-
 
|-
−
| || |Nun wiederholen wir Schritt 2 und 3 und zeichnen wieder eine Senkrecht im Mittelpunkt der ebene gezeichneten Strecke mit je 1,5cm nach oben und unten. Diese vier Eckpunkte verbinden wir wieder zu einem schrägen Kreis.
+
| [[Bild:Schritt_5.JPG|300px]]|| |Nun wiederholen wir Schritt 2 und 3 und zeichnen wieder eine Senkrecht im Mittelpunkt der ebene gezeichneten Strecke mit je 1,5cm nach oben und unten. Diese vier Eckpunkte verbinden wir wieder zu einem schrägen Kreis.
 
|  
 
|  
 
|}
 
|}
Zeile 67: Zeile 58:
 
! Schritt 6 !!  
 
! Schritt 6 !!  
 
|-
 
|-
−
| || |Nun radieren wir noch unnötig Hilfslinien wieder weg und beschriften den Zylinder.  
+
| [[Bild:Schritt_6.JPG|300px]]|| |Nun radieren wir noch unnötig Hilfslinien wieder weg und beschriften den Zylinder.  
 
|  
 
|  
 
|}
 
|}
Zeile 84: Zeile 75:
 
Löse folgende Aufgaben in deinem Schulheft, schreibe die Ergebnisse aber auch auf deinen Laufzettel!
 
Löse folgende Aufgaben in deinem Schulheft, schreibe die Ergebnisse aber auch auf deinen Laufzettel!
 
:a) Eine Regentonne ist 15 dm hoch und hat einen Radius von 3 dm. Wie groß ist das Fassungsvermögen (Volumen) der Regentonne? Wie viel Liter Wasser passen in die Regentonne?(Hilfe: 1dm³=1l)Berechne!
 
:a) Eine Regentonne ist 15 dm hoch und hat einen Radius von 3 dm. Wie groß ist das Fassungsvermögen (Volumen) der Regentonne? Wie viel Liter Wasser passen in die Regentonne?(Hilfe: 1dm³=1l)Berechne!
−
:b) Das Volumen eines Plastikrohres ist 47,1 cm³. Die Höhe ist 15 cm. Welche der folgenden behauptungen ist wahr?
+
:b) Das Volumen eines Plastikrohres ist 47,1 cm³. Die Höhe ist 15 cm. Welche der folgenden Behauptungen ist wahr? Begründe deine Antwort.
 
:Die Grundfläche G des Zylinders ist  
 
:Die Grundfläche G des Zylinders ist  
 
::- größer als 3,25 cm²  
 
::- größer als 3,25 cm²  
Zeile 91: Zeile 82:
 
::- größer als 3,18 cm²
 
::- größer als 3,18 cm²
 
Hilfe: <span style="background:#000000"><math>G=\frac{V}{h_K}</math></span>
 
Hilfe: <span style="background:#000000"><math>G=\frac{V}{h_K}</math></span>
 +
</div>
 +
<br>
 +
<div style="border: 2px solid green; background-color:#ffffff; padding:7px;">
 +
Nun hast du den fünften Teil des Lernpfades geschafft. Gib deinen Laufzettel bei mir ab.
 +
In der nächsten Stunde werden wir noch einmal all das wiederholen, was du diese Woche neu gelernt hast.
 +
<br>
 +
Als Hausaufgabe löse bitte die Aufgaben, die ich dir austeile auf einem extra Blatt, das du morgen abgibst.
 +
<br>
 +
Weiter geht es mit dem Aufgabenblatt rund um den Zylinder: [[../Zylinder queerbeet|Zylinder queerbeet]]
 
</div>
 
</div>

Aktuelle Version vom 30. Mai 2010, 10:26 Uhr

Hier werden wir uns nun um das Volumen des Zylinders kümmern. Du benötigst dafür dein Schulheft, Geodreieck und Stifte

1. Aufgabe

Wir haben im ersten Lernpfad dreiseitige Prismen wiederholt. Dort haben wir auch festgestellt, dass die Formel für das Volumen eines Körpers in der Grundform immer gleich ist, nämlich V=G\cdot h_K. Diese Formle gilt ebenso für unseren neune Körper Zylinder. Nun benötigen wir aber noch die Grundfläche G. Diese besteht bei unserem Zylinder aus einem Kreis. 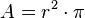Der Flächeninhalt des Kreises lässt sich mit A=r^2\cdot \pi darstellen. 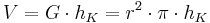Also können wir die Formel für das Zylindervolumen zusammenfügen: V=G\cdot h_K=r^2\cdot \pi\cdot h_K.

 


2. Aufgabe


Nun sollst du dein Schulheft zur Hand nehmen und mit Hilfe der folgenden Anleitung einen Zylinder mit dem Radius 3cm und der Höhe 7cm in das Heft zeichnen. Schreibe darüber als Überschrift "Volumen des Zylinders".

Schritt 1
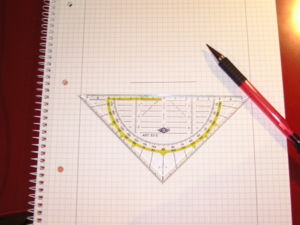Schritt 1.JPG Als erstes lässt du ca. 10cm Platz und zeichnest dann eine waagrechte Linie mit der Länge 2r also 6cm.


Schritt 2
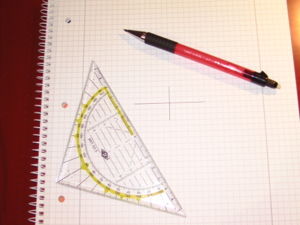Schritt 2.JPG Nun zeichnest du eine senkrechte Linie im Mittelpunkt der ersten Linie mit je 1,5cm Länge (nach oben und unten).


Schritt 3
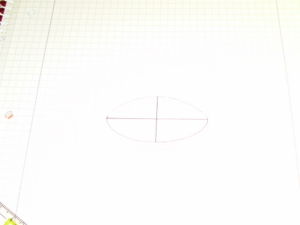Schritt 3.JPG Als nächstes verbindest du die vier Eckpunkte zu einem schrägen Kreis bzw. zu einer Ellipse.


Schritt 4
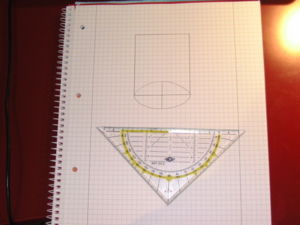Schritt 4.JPG Jetzt trägst du an den zwei Eckpunkten rechts und links jeweils die Höhe des Zylinders (7cm) senkrecht an und verbindest die Enden.


Schritt 5
Schritt 5.JPG Nun wiederholen wir Schritt 2 und 3 und zeichnen wieder eine Senkrecht im Mittelpunkt der ebene gezeichneten Strecke mit je 1,5cm nach oben und unten. Diese vier Eckpunkte verbinden wir wieder zu einem schrägen Kreis.


Schritt 6
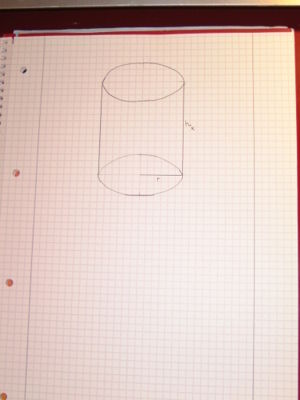Schritt 6.JPG Nun radieren wir noch unnötig Hilfslinien wieder weg und beschriften den Zylinder.



Nuvola apps kig.png   Merke
Volumen des Zylinders: V=G\cdot h_K=r^2\cdot \pi\cdot h_K

Übertrage diese Formel bitte in dein Schulheft unter die eben angefertigte Zeichnung.


3. Aufgabe

Löse folgende Aufgaben in deinem Schulheft, schreibe die Ergebnisse aber auch auf deinen Laufzettel!

a) Eine Regentonne ist 15 dm hoch und hat einen Radius von 3 dm. Wie groß ist das Fassungsvermögen (Volumen) der Regentonne? Wie viel Liter Wasser passen in die Regentonne?(Hilfe: 1dm³=1l)Berechne!
b) Das Volumen eines Plastikrohres ist 47,1 cm³. Die Höhe ist 15 cm. Welche der folgenden Behauptungen ist wahr? Begründe deine Antwort.
Die Grundfläche G des Zylinders ist
- größer als 3,25 cm²
- kleiner als 3,15 cm²
- genau 3 cm²
- größer als 3,18 cm²

Hilfe: 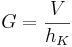G=\frac{V}{h_K}


Nun hast du den fünften Teil des Lernpfades geschafft. Gib deinen Laufzettel bei mir ab. In der nächsten Stunde werden wir noch einmal all das wiederholen, was du diese Woche neu gelernt hast.
Als Hausaufgabe löse bitte die Aufgaben, die ich dir austeile auf einem extra Blatt, das du morgen abgibst.
Weiter geht es mit dem Aufgabenblatt rund um den Zylinder: Zylinder queerbeet

Von „http://dmuw.zum.de/index.php?title=Lernpfade/Zylinder/Volumen_des_Zylinders&oldid=19427“