Lernpfad3 Seite 3: Unterschied zwischen den Versionen
| Zeile 42: | Zeile 42: | ||
<div style="border: 2px solid #008B45; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid #008B45; background-color:#ffffff; padding:7px;"> | ||
| − | + | Nun ist es deine Aufgabe, die fehlenden Teile der Raupe (rote Kreise) mit den richtigen Brüchen <u>im Kopf</u> auszurechnen. | |
| − | + | ||
| − | + | ||
| − | < | + | |
| − | + | ||
| − | + | ||
| + | Überprüfe dein Ergebnis, indem du auf das Kästchen darunter klickst. Es erscheint dann die Lösung. | ||
| − | + | Sei bitte ehrlich und drücke das Kästchen erst, wenn du das Ergebnis im Kopf berechnet hast. | |
| − | + | ||
| − | + | ||
| − | + | ||
| + | '''a)''' | ||
| + | <ggb_applet height="170" width="800" showResetIcon="true" filename="Ann-Kathrin_Hey_Raupe1.ggb" /> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br>'''b)''' | ||
| + | <br> | ||
| + | <ggb_applet height="170" width="800" showResetIcon="true" filename="Ann-Kathrin_Hey_Raupe2.ggb" /> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
</div> | </div> | ||
Version vom 3. Januar 2010, 18:21 Uhr
2.Station: Addition von gleichnamigen Brüchen
Zum Frühstück hat Svenja schon  Liter Schokomilch getrunken. Nach Unterrichtsschluss hat sie auch ihre
Liter Schokomilch getrunken. Nach Unterrichtsschluss hat sie auch ihre  Liter Flasche Apfelsaftschorle leer getrunken.
Liter Flasche Apfelsaftschorle leer getrunken.
Wie viel Liter hat Svenja insgesamt getrunken?
Welchen Rechenweg würdest du nehmen um die beiden Brüche zu addieren
(! +
+  =
= 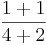 =
= 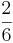 =
=  )
)
(! +
+  =
=  +
+  =
=  =
=  )
)
( +
+  =
=  +
+  =
= 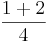 =
=  )
)
Man kann also sagen, dass die beiden Brüche addiert werden, nachdem sie durch Erweitern auf denselben Hauptnenner gebracht werden (hier wurde mit 2 erweitert).
Kreuze die richtige Lösung an! BEACHTE: Es können auch mehrere Lösungen richtig sein!
1) 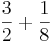 (!
(! ) (!
) (! ) (!
) (!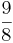 ) (!
) (!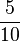 ) (
) (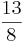 )
)
2) 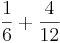 (!
(!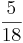 ) (
) (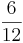 ) (!
) (!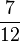 ) (
) ( ) (!
) (! )
)
3) 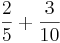 (!
(!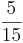 ) (
) (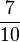 ) (!
) (! ) (!
) (!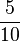 ) (!
) (! )
)
Nun ist es deine Aufgabe, die fehlenden Teile der Raupe (rote Kreise) mit den richtigen Brüchen im Kopf auszurechnen.
Überprüfe dein Ergebnis, indem du auf das Kästchen darunter klickst. Es erscheint dann die Lösung.
Sei bitte ehrlich und drücke das Kästchen erst, wenn du das Ergebnis im Kopf berechnet hast.
a)
b)
Damit du immer weisst, wie du bei der Addition ungleichnamiger Brüche vorgehen musst, ist es deine Aufgabe den folgenden Lückentext mit den richtigen Wörtern auszufüllen. Das Beispiel nebenan soll dir eine kleine Hilfe sein.
| Allgemein: |
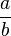 + + 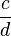 = = 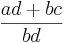
|
Beispiel "Messbecher":  Liter +
Liter +  Liter =
Liter =  Liter +
Liter +  Liter =
Liter =  Liter =
Liter = 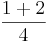 Liter =
Liter =  Liter
Liter

 +
+ 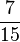
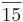
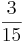 +
+ 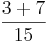 =
=