SSS-Satz-2: Unterschied zwischen den Versionen
Aus DMUW-Wiki
K |
K |
||
| Zeile 26: | Zeile 26: | ||
{{Merke| | {{Merke| | ||
'''SSS-Satz'''<br /> | '''SSS-Satz'''<br /> | ||
| − | Dreiecke sind zueinander '''kongruent''', wenn sie in den '''Längen''' ihrer '''drei Seiten''' übereinstimmen (Seite-Seite-Seite-Satz). | + | Dreiecke sind zueinander '''kongruent''', wenn sie in den '''Längen''' ihrer '''drei Seiten''' übereinstimmen (Seite-Seite-Seite-Satz).<br /> |
| + | <u>''oder:''</u> Man kann ein Dreieck eindeutig konstruieren wenn die Längen aller drei Seiten gegeben sind. | ||
}} | }} | ||
| − | {{Aufgabe-Mathe|Übertrage den Satz auf deinen <u>Laufzettel</u> | + | {{Aufgabe-Mathe|Übertrage den Satz auf deinen <u>Laufzettel</u>!}} |
<br /> | <br /> | ||
<br /> | <br /> | ||
[[Benutzer:Kathrin_Fuchs/SSS_und_SWS/SSS-Satz-3|<math>\Rightarrow</math> Wenn du den Satz abgeschrieben hast, gibt es hier eine Aufgabe dazu.]] | [[Benutzer:Kathrin_Fuchs/SSS_und_SWS/SSS-Satz-3|<math>\Rightarrow</math> Wenn du den Satz abgeschrieben hast, gibt es hier eine Aufgabe dazu.]] | ||
Version vom 17. Februar 2010, 12:23 Uhr
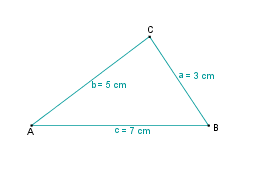
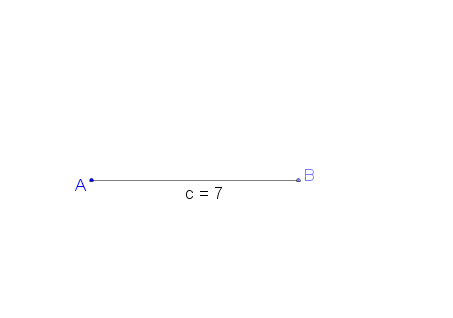
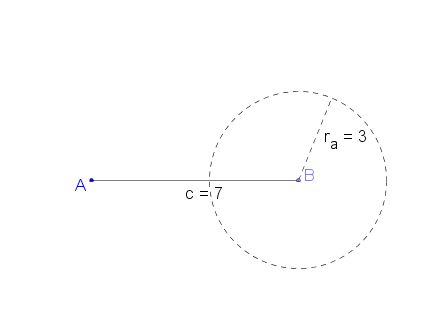
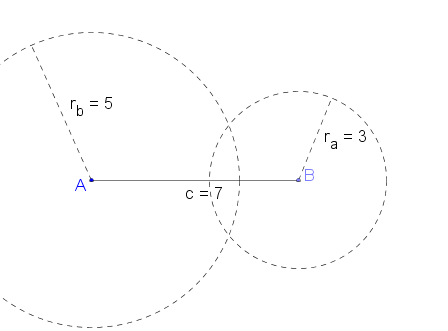
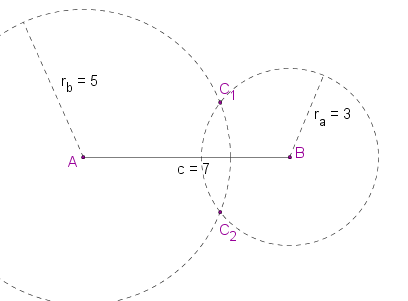
Wir wissen jetzt also, dass das Dreieck mit den Seitenlängen a = 3 cm, b = 5 cm und c = 7 cm konstruierbar ist!
| Um das Dreieck zu konstruieren fertigen wir zunächst eine Skizze an. Dazu zeichnen wir ein beliebiges Dreieck und markieren alle gegebenen Größen farbig. | 
|
| Wir beginnen mit der Grundseite c = 7 cm. | 
|
| Dann zeichnen wir um den Punkt B einen Kreis mit Radius a = 3 cm. | 
|
| Danach zeichnen wir einen Kreis mit Radius b = 5 cm um A. | 
|
| Die Kreise schneiden sich in 2 Punkten. Diese Schnittpunkte nennen wir C1 und C2. | 
|
| Um ein Dreieck zu erhalten verbinden wir jetzt noch die Punkte A, B und C1, bzw. A, B und C2. | 
|
| Somit erhalten wir zwei kongruente Dreiecke. | 
|
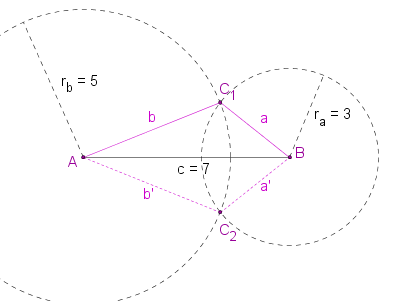
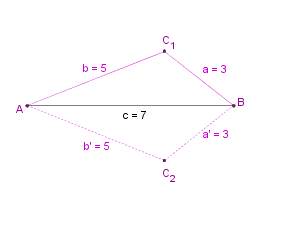
Du glaubst mir nicht, dass die Dreiecke kongruent sind? Dann schau selbst:
Zur Erinnerung: Wenn man zwei Dreiecke durch Achsenspiegelung aufeinander abbilden kann sagt man, die Dreiecke sind kongruent.
 Merke
SSS-Satz |
Aufgabe
Übertrage den Satz auf deinen Laufzettel! |
Wenn du den Satz abgeschrieben hast, gibt es hier eine Aufgabe dazu.
