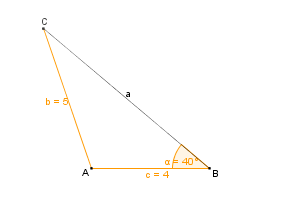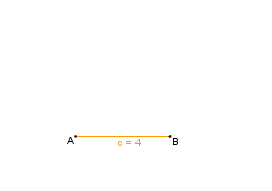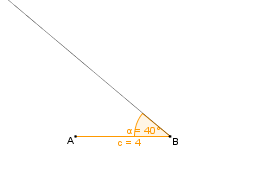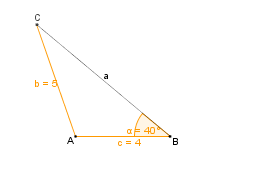SSW g-Satz-1: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: <div style="border: 2px solid #0000ee; background-color:#ffffff; padding:7px;"> {| class="wikitable" |- | Bild:KS_Dreieck2.JPG || Wie konstruiert man ein Drei...) |
K |
||
| Zeile 24: | Zeile 24: | ||
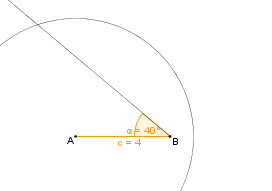
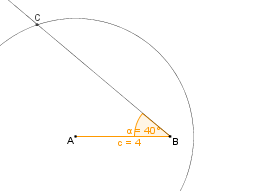
| Der Kreis schneidet die Halbgerade des Winkels im Punkt C. || [[Bild:KS_Schritt4_SsW.png]] | | Der Kreis schneidet die Halbgerade des Winkels im Punkt C. || [[Bild:KS_Schritt4_SsW.png]] | ||
|- | |- | ||
| − | | Wir verbinden die Punkte B und C und erhalten ein eindeutig festgelegtes Dreieck. || [[Bild:KS_Schritt5_SsW.png]] | + | | Wir verbinden die Punkte B und C sowie A und C und erhalten dadurch ein eindeutig festgelegtes Dreieck. || [[Bild:KS_Schritt5_SsW.png]] |
|} | |} | ||
</div> | </div> | ||
Version vom 19. Februar 2010, 21:50 Uhr
 |
Wie konstruiert man ein Dreieck, von dem zwei Seitenlängen und das Maß des Gegenwinkels der größeren Seite gegeben sind? |
Wir wollen ein Dreieck konstruieren, von dem die Seitenlängen b = 5 cm und c = 4 cm,
sowie der Gegenwinkel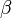 
40° gegeben sind.
Da von dem Dreieck zwei Seitenlängen und der Gegenwinkel der größeren Seite gegeben sind,
müssen wir nicht nachprüfen ob das Dreieck überhaupt konstruierbar ist!
| Um das Dreieck zu konstruieren fertigen wir zunächst eine Skizze an. Dazu zeichnen wir ein beliebiges Dreieck und markieren alle gegebenen Größen farbig. | 
|
| Wir beginnen mit der Grundseite c = 4 cm. | 
|
| Am Punkt B tragen wir den Winkel 40° im Uhrzeigersinn ab. |
|
| Um den Punkt A zeichnen wir einen Kreis mit Radius b = 5 cm. | 
|
| Der Kreis schneidet die Halbgerade des Winkels im Punkt C. | 
|
| Wir verbinden die Punkte B und C sowie A und C und erhalten dadurch ein eindeutig festgelegtes Dreieck. | 
|
 Merke
SSWg-Satz |
Aufgabe
Übertrage den Satz auf deinen Laufzettel! |
Wenn du den Satz abgeschrieben hast, gibt es hier eine Aufgabe dazu.
