Profiaufgaben: Unterschied zwischen den Versionen
| Zeile 33: | Zeile 33: | ||
|} | |} | ||
<br /><br /><br /> | <br /><br /><br /> | ||
| − | + | <big>'''[[../| <math>\Leftarrow</math>zurück zum Aufgabenmenü <math>\Leftarrow</math> ]]'''</big> | |
Aktuelle Version vom 13. Juli 2010, 13:42 Uhr
Wie groß ein Fußballfeld bei internationalen Wettbewerben sein darf, schreibt die Weltfußballorganisation (FIFA) vor. Die Breite muss zwischen 64 m und 73 m betragen und die Länge zwischen 100 m und 110 m.
Somit ist der Wert des minimalen Flächeninhalts 6400 m², und der maximale Flächeninhalt 8030 m².
32 Schwimmbecken der Größe 200 m² passen in die Mindestgröße eines Fußballfeldes hinein. Der maximalen Größe entsprechen sogar mehr als 40 von solchen Schwimmbecken. Das sind damit 8 mehr als bei der Mindestgröße!
Wenn du fertig bist, dann drücke einfach auf "prüfen" und du siehst, ob du alles richtig gelöst hast!
|
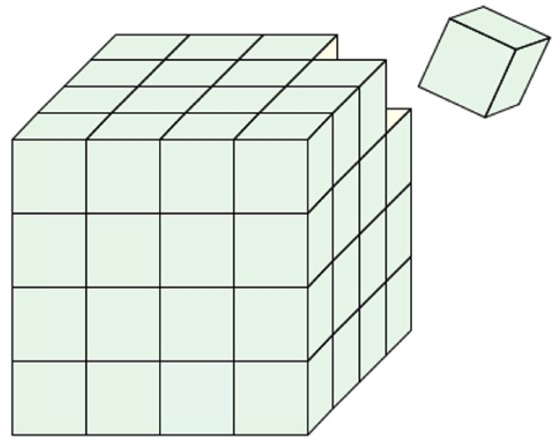
Der nebenstehende grüne Würfel mit 12 cm Kantenlänge wird in kleine Würfel mit 3 cm Kantenlänge zerschnitten.
Wie viele Würfel entstehen? (!60) (64) (!62) (!68) Wie viele Würfel, die nur zwei grüne Flächen haben, entstehen? (!20) (!22) (24) (!26) Wie viele Würfel entstehen, die gar keine grüne Fläche haben? (!4) (!6) (8) (!10) |
 |
zurück zum Aufgabenmenü 
