Eigenschaften der Achsenspiegelung: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
Zeile 56: Zeile 56:
 
| <ggb_applet height="400" width="400" showResetIcon="true" filename="Kreis.ggb" /> <br> Ziehe am Mittelpunkt M! || <ggb_applet height="400" width="400" showResetIcon="true" filename="Parallele.ggb" /> <br> Bewege die Gerade g!||  
 
| <ggb_applet height="400" width="400" showResetIcon="true" filename="Kreis.ggb" /> <br> Ziehe am Mittelpunkt M! || <ggb_applet height="400" width="400" showResetIcon="true" filename="Parallele.ggb" /> <br> Bewege die Gerade g!||  
 
|-
 
|-
−
| <ggb_applet height="400" width="400" showResetIcon="true" filename="StreckAB.ggb" /> <br> Ziehe am Punkt B!|| <ggb_applet height="400" width="400" showResetIcon="true" filename="<ggb_applet width="400" height="400"  version="3.2" ggbBase64<ggb_applet width="400" height="400"  version="3.2" Ziehe am Punkt C!|| ggbBase64="UEsDBBQACAAIAKZ+cz4AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3VnNcts2ED43T8Hy0JtpAiAAYiolIyfpTGaSplOl6UxuFAlJqChSJSFbzls1D5Jn6gIg9WspkqNJ7PhgSgC42P1298Ni1Xm2mObetaxqVRZdHwWh78kiLTNVjLr+XA8vYv/Z0yedkSxHclAl3rCsponu+iTAvhmfq6dPfurU4/LGS3K75L2SN11/mOS19L16Vskkq8dS6o3xZL5QuUqq27eDf2Sq69WEE/KqmM1hF13NYSydZq9V3X69tBvOcqVfqGuVycrLy7TrMwqqw6f3stIqTfKuH4VuBHd9vDUJQ8TMjstKfSwLbZavhA9hxPNq9VECItiMdS6toR05T3OVqaQwxlg9YJHn3ahMj7t+LDCIlGo0Bl0p4k5aWpZV1r+ttZx6iw+yKkEdIoKYoJBjzihnIob3bt0UwTSgIRU85FxEEY4YgAgagyqEBVzQKBQUx4zGjMBLe6fs1vK6L7UGV9ZespArkEeVylpwzedX9VWZZ8vpWakK/TyZ6Xllw4A0Q319azYD3CpjY68Y5bIZAwPSsUwng3LRd7gRJ/rd7cy+YvUZjJ6XeVl5lfEIhQXNc+Cedo1RdLkqtGtCu6KRYYQu55FBfNQ8B+5pV+WqcKo1hqPWaBS226jaMwMg3ETv0vg8GUiIBt+bF0q/br9A1EwaU5F74ff5dABpsx43S5noXDI7l1sR15nIqpC5i6sCXDsv57V3beLX7WUVyWSqpvDVTTSQJMZdf4ECbjSTo0q2irukc4DZ2XA9dreGO5etEkaHGnRNNbAH2KONLX+rYiJzk+Ia0qvrQwgpHCIwMUs0zPtG8E1ZTSwrvJML7SWD8trMeICMge2DkmPw3NT7Y15MtHf1s91W5nIqITO1DSkbkUtor/wlDZWWUdrwbuZXToLpZfhQZKPHPJoQBP6ZjRMwNGgQyJNbYJh1TKzEN2W2iVRSAOIWBkj0mRFgfDqTMmtYVTeJ4M1ApE2rNYdZnGtvYd4jIaERIhhRHMaUG2oALguYICzGFPMQM2LQ/OgE2/ddehousjqRJnYcYF+Arv+NoXs7HNZSG1svUGyNA2u+AbIX2CyG7ezzFPTScjpNiswrkils1JcjM25RU+aY8pLQBKCXIAOmQ2qu24nESWtk7PiibqS1aCf+Jn3pMbBEIevacqxeZ9P9Lluzf91nm2x671BfQYq3ozKyAAPSW0Fs8RaBgBMtgvOOhyIihG9T9QFb5b+FW1M7wlRTKABSpZdw58bzrwoN9CktHe2y4kTKmTmO3hbvqqSoTSXj1qyx7VEZ0/txyIYJjDjjlMURxhxT678wiFAMM5zEkQg5zJw/X/ouX3o7+TI4LV8GjylfUEBjRKDsY4iGAlMeN4S05QZi8YY0wjBMYiFCxliIRfSQM2bT67Y43PJ5r+VIL8GGMbdd//m/w763FczSabDavA/6zBu8UUCAV4CRkIgogw9f8vvdiercjsJdx6ODjl8dbFg4HiR3hsVOiXrAi0mVriVaO5hDlfSnHOZyYWG+H4s932WxzXL1iKx4ECzWnuv01HP9EDovfjR0wnOi8/JBo3M0NigQnDMoXARwL6JMuPqFBTTiiEcsJPCfCnE+4H77oYGDEwvqBs6gvIuEiFFT+N2zcHgNBLl1grx0J8hvO0dHevjkMFy7hDjdXzJEX1sytG2Npso7S9UgoByDOpvSKEYcQ5Gwkc9wiQoYJhSzmIo4xDFmB86XbQMPVQn7PfNGVVVZ3X0DSnd8c/VLMivrXw97aOs637xy/+P7jFUbCRhFPKYhRyLGODatra+/kh+BaH8fov3TEe1/c0RX5ZDDC+Hj4KaBoJRgU79RIGAi2kv75l90drh7++DunQ537zvCfYG4Y+ODbZX1+DbhGwlGzC0jZmzPLZB8FeR72iYNTu5isMJ5A//stCth9piuhDstlCbatxoorLkRwo09iuMIYYEEFfxh91COCYDeMQEgTwsA+ZgC4GK7KXCwJxAFIcFxxAnlITJ9tMfj/7s6Anemv+0O9PaEwudPJ/UIPn2pR4Dj79UkuKDRA+kSXK7/jGN/7Gx+7X36P1BLBwgAykYABwYAAB8eAABQSwECFAAUAAgACACmfnM+AMpGAAcGAAAfHgAADAAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAABAAEAOgAAAEEGAAAAAA==" <br>
+
| <ggb_applet height="400" width="400" showResetIcon="true" filename="StreckAB.ggb" /> <br> Ziehe am Punkt B!|| <ggb_applet height="400" width="400" showResetIcon="true" filename="<ggb_applet width="400" height="400"  version="3.2" ggbBase64<ggb_applet width="400" height="400"  version="3.2" Ziehe am Punkt C!|| ggbBase64="UEsDBBQACAAIAKZ+cz4AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3VnNcts2ED43T8Hy0JtpAiAAYiolIyfpTGaSplOl6UxuFAlJqChSJSFbzls1D5Jn6gIg9WspkqNJ7PhgSgC42P1298Ni1Xm2mObetaxqVRZdHwWh78kiLTNVjLr+XA8vYv/Z0yedkSxHclAl3rCsponu+iTAvhmfq6dPfurU4/LGS3K75L2SN11/mOS19L16Vskkq8dS6o3xZL5QuUqq27eDf2Sq69WEE/KqmM1hF13NYSydZq9V3X69tBvOcqVfqGuVycrLy7TrMwqqw6f3stIqTfKuH4VuBHd9vDUJQ8TMjstKfSwLbZavhA9hxPNq9VECItiMdS6toR05T3OVqaQwxlg9YJHn3ahMj7t+LDCIlGo0Bl0p4k5aWpZV1r+ttZx6iw+yKkEdIoKYoJBjzihnIob3bt0UwTSgIRU85FxEEY4YgAgagyqEBVzQKBQUx4zGjMBLe6fs1vK6L7UGV9ZespArkEeVylpwzedX9VWZZ8vpWakK/TyZ6Xllw4A0Q319azYD3CpjY68Y5bIZAwPSsUwng3LRd7gRJ/rd7cy+YvUZjJ6XeVl5lfEIhQXNc+Cedo1RdLkqtGtCu6KRYYQu55FBfNQ8B+5pV+WqcKo1hqPWaBS226jaMwMg3ETv0vg8GUiIBt+bF0q/br9A1EwaU5F74ff5dABpsx43S5noXDI7l1sR15nIqpC5i6sCXDsv57V3beLX7WUVyWSqpvDVTTSQJMZdf4ECbjSTo0q2irukc4DZ2XA9dreGO5etEkaHGnRNNbAH2KONLX+rYiJzk+Ia0qvrQwgpHCIwMUs0zPtG8E1ZTSwrvJML7SWD8trMeICMge2DkmPw3NT7Y15MtHf1s91W5nIqITO1DSkbkUtor/wlDZWWUdrwbuZXToLpZfhQZKPHPJoQBP6ZjRMwNGgQyJNbYJh1TKzEN2W2iVRSAOIWBkj0mRFgfDqTMmtYVTeJ4M1ApE2rNYdZnGtvYd4jIaERIhhRHMaUG2oALguYICzGFPMQM2LQ/OgE2/ddehousjqRJnYcYF+Arv+NoXs7HNZSG1svUGyNA2u+AbIX2CyG7ezzFPTScjpNiswrkils1JcjM25RU+aY8pLQBKCXIAOmQ2qu24nESWtk7PiibqS1aCf+Jn3pMbBEIevacqxeZ9P9Lluzf91nm2x671BfQYq3ozKyAAPSW0Fs8RaBgBMtgvOOhyIihG9T9QFb5b+FW1M7wlRTKABSpZdw58bzrwoN9CktHe2y4kTKmTmO3hbvqqSoTSXj1qyx7VEZ0/txyIYJjDjjlMURxhxT678wiFAMM5zEkQg5zJw/X/ouX3o7+TI4LV8GjylfUEBjRKDsY4iGAlMeN4S05QZi8YY0wjBMYiFCxliIRfSQM2bT67Y43PJ5r+VIL8GGMbdd//m/w763FczSabDavA/6zBu8UUCAV4CRkIgogw9f8vvdiercjsJdx6ODjl8dbFg4HiR3hsVOiXrAi0mVriVaO5hDlfSnHOZyYWG+H4s932WxzXL1iKx4ECzWnuv01HP9EDovfjR0wnOi8/JBo3M0NigQnDMoXARwL6JMuPqFBTTiiEcsJPCfCnE+4H77oYGDEwvqBs6gvIuEiFFT+N2zcHgNBLl1grx0J8hvO0dHevjkMFy7hDjdXzJEX1sytG2Npso7S9UgoByDOpvSKEYcQ5Gwkc9wiQoYJhSzmIo4xDFmB86XbQMPVQn7PfNGVVVZ3X0DSnd8c/VLMivrXw97aOs637xy/+P7jFUbCRhFPKYhRyLGODatra+/kh+BaH8fov3TEe1/c0RX5ZDDC+Hj4KaBoJRgU79RIGAi2kv75l90drh7++DunQ537zvCfYG4Y+ODbZX1+DbhGwlGzC0jZmzPLZB8FeR72iYNTu5isMJ5A//stCth9piuhDstlCbatxoorLkRwo09iuMIYYEEFfxh91COCYDeMQEgTwsA+ZgC4GK7KXCwJxAFIcFxxAnlITJ9tMfj/7s6Anemv+0O9PaEwudPJ/UIPn2pR4Dj79UkuKDRA+kSXK7/jGN/7Gx+7X36P1BLBwgAykYABwYAAB8eAABQSwECFAAUAAgACACmfnM+AMpGAAcGAAAfHgAADAAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAABAAEAOgAAAEEGAAAAAA==" |}
−
|}
+
  
  

Version vom 19. März 2011, 16:16 Uhr


Mathematik-digital Pfeil-3d.png
Lernpfad

Teil 2: Eigenschaften der Achsenspiegelung

  • Zeitbedarf: 45 Min.
  • Material: dein Heft, Stifte und ein Geodreieck
Spiegel7.jpg

Im Teil 1 des Lernpfads hast du ja schon einige grundlegende Dinge über das Thema Achsenspiegelung gelernt. Im zweiten Teil soll es jetzt um die Eigenschaften der Achsenspiegelung gehen.

Schreibe dir wieder alle Merksätze in dein Heft!

1.Station: Besondere Punkte und Geraden

1. Aufgabe

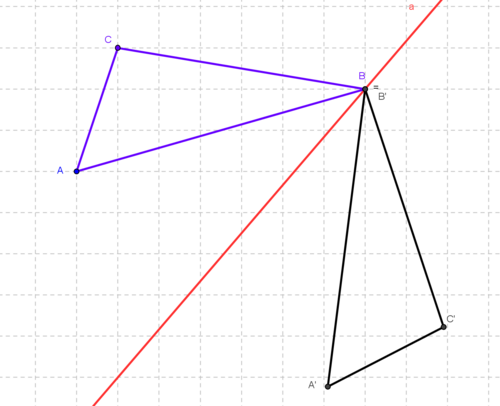
Du siehst hier eine Achsenspiegelung bei der ein Punkt des Urdreiecks auf der Spiegelachse liegt. Das heißt Urpunkt und Bildpunkt sind gleich, B=B'.

Fixpunkt.png

Finde die unverdrehte Lösung zu den verdrehten Wörtern! Achte dabei auch auf die richtige Schreibweise.

Liegt ein Punkt bei einer Achsenspiegelung genau auf der Spiegelachse, nennt man einen solchen Punkt Fixpunkt.

Dabei wird jeder Fixpunkt auf sich selbst abgebildet. Alle Punkte auf der Spiegelachse sind Fixpunkte.

Daher ist die Spiegelachse eine Fixpunktgerade.

Das war ganz schön schwierig, oder? Wenn du nicht alle Wörter herausgefunden hast, sieh dir den Merksatz an!


Hier findest du den Merksatz!


Nuvola apps kig.png   Merke

Fixpunkt und Fixpunktgerade

  • Ein Punkt, der sich genau auf der Spiegelachse befindet, heißt Fixpunkt.
    Spiegel2.jpg
  • Jeder Fixpunkt wird auf sich selbst abgebildet, somit sind in diesem Fall Urpunkt und Bildpunkt gleich.
  • Die Spiegelachse besteht ausschließlich aus Fixpunkten.
  • Daher nennt man die Spiegelachse auch Fixpunktgerade.

2.Station: Wichtige Eigenschaften der Achsenspiegelung

Jetzt wollen wir uns die besonderen Eigenschaften der Achsenspiegelung anschauen. Es gibt fünf Eigenschaften, die du kennen solltest, um eine Achsenspiegelung richtig ausführen zu können! Also los geht´s!

Vielleicht helfen dir die folgenden Applets die Eigenschaften herauszufinden.

Eigenschaften der Achsenspiegelung

Ziehe am Mittelpunkt M!

Bewege die Gerade g!

Ziehe am Punkt B!
Von „http://dmuw.zum.de/index.php?title=Lernpfade/Achsenspiegelung/Eigenschaften_der_Achsenspiegelung&oldid=29265“