Untergruppenkriterium: Unterschied zwischen den Versionen
| Zeile 22: | Zeile 22: | ||
"<math> \Leftarrow </math>" : | "<math> \Leftarrow </math>" : | ||
| − | Wegen <math> a \ast b \in U </math> ist U abgeschlossen. Da für ein Element <math> a \in U </math> auch gilt, dass auch <math> a^{-1} \in U </math> existieren inverse Elemte. Da U nicht leer existiert ein Element <math>u \in U </math>. Da auch <math> u^{-1} \in U </math> und auch <math> u \ast u^{-1} \in U </math> ist auch <math> e \in U <math>. D.h. das neutrale Element der Obergruppe G ist in U enthalten. Es fehlt nur noch die Assoziativität. Die Verknüpfung in G ist assoziativ, da G eine Gruppe ist. Die Verknüpfung in U ist nur eine Einschränkung der Verknüpfung von G. Und behält die Assoziativität. Denn die Elemente aus U werden wie in der Gruppe G verknüpft und verlieren die Assoziativität nicht. | + | Wegen <math> a \ast b \in U </math> ist U abgeschlossen. Da für ein Element <math> a \in U </math> auch gilt, dass auch <math> a^{-1} \in U </math> existieren inverse Elemte. Da U nicht leer existiert ein Element <math>u \in U </math>. Da auch <math> u^{-1} \in U </math> und auch <math> u \ast u^{-1} \in U </math> ist auch <math> e \in U </math>. D.h. das neutrale Element der Obergruppe G ist in U enthalten. Es fehlt nur noch die Assoziativität. Die Verknüpfung in G ist assoziativ, da G eine Gruppe ist. Die Verknüpfung in U ist nur eine Einschränkung der Verknüpfung von G. Und behält die Assoziativität. Denn die Elemente aus U werden wie in der Gruppe G verknüpft und verlieren die Assoziativität nicht. |
Somit ist U eine Gruppe. | Somit ist U eine Gruppe. | ||
Aktuelle Version vom 28. November 2018, 00:39 Uhr
Aussage
Sei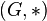 
eine Gruppe und U eine Teilmenge von G, also 
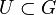und 
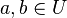. Dann gilt:
Definitionen
Was bedeutet "mit der eingeschränkten Verknüpfung von G auf U"? G ist eine Gruppe, d.h. es gibt eine Verknüpfung auf G, also eine Abbildung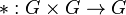 
.
Wir haben eine Abbildung, d.h. wir können Einschränkungen dieser Abbildung betrachten. In unserem Fall betrachten wir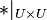 
.
Ist U mit dieser Einschränkung eine Gruppe (Abgeschlossenheit + Assoziativität + neutrales Element + inverse Elemente), dann sagen wir: U ist eine Untergruppe von G und schreiben: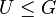 
Beweis
Es liegt eine Äquivalenz vor, d.h. wir müssen zwei Implikationen zeigen:
"
" :
Sei U eine Gruppe. U ist eine Gruppe und damit abgeschlossen. Abgeschlossenheit heißt dass die Verknüpfung wieder nach U abbildet: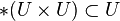 
, also gilt 
: 
.
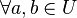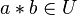U ist eine Gruppe, d.h. es existieren inverse Elemente. Somit gilt für alle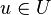 
, dass ebenfalls 
.
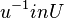U ist eine Gruppe, d.h. es existiert ein neutrales Element, d.h. es gibt mindestens ein Element. Somit ist U nicht leer.
"
" :
Wegen 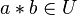ist U abgeschlossen. Da für ein Element 
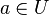auch gilt, dass auch 
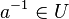existieren inverse Elemte. Da U nicht leer existiert ein Element 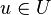. Da auch 
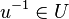und auch 
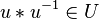ist auch 
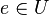. D.h. das neutrale Element der Obergruppe G ist in U enthalten. Es fehlt nur noch die Assoziativität. Die Verknüpfung in G ist assoziativ, da G eine Gruppe ist. Die Verknüpfung in U ist nur eine Einschränkung der Verknüpfung von G. Und behält die Assoziativität. Denn die Elemente aus U werden wie in der Gruppe G verknüpft und verlieren die Assoziativität nicht.
Somit ist U eine Gruppe.
Aspekte
- Die Verknüpfung in U ist die Einschränkung von G auf U. Die inversen Element sind eindeutig bestimmt. (Eindeutigkeit der inversen Elemente in einer Gruppe). D.h. für ein 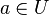gibt es nur ein
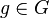mit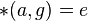 
. U ist eine Gruppe, d.h. es gibt für alle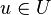
Also ist für ein Element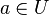
- Es existieren inverse Elemente. Warum kann man hier nicht folgern, dass U nicht leer ist.
