Zusammenfassung zur Zerlegungsgleichheit: Unterschied zwischen den Versionen
Aus DMUW-Wiki
(Bilder zur Ergänzungsgleichheit eingefügt) |
(→Ergänzungsgleichheit von Figuren: text eingefügt) |
||
| Zeile 35: | Zeile 35: | ||
===Ergänzungsgleichheit von Figuren=== | ===Ergänzungsgleichheit von Figuren=== | ||
| − | |||
| − | |||
| − | + | '''''Zeige, dass das Rechteck und das Trapez zerlegungsgleich sind''''' | |
| + | Applet | ||
| − | + | '''''Ergänze das Trapez und das Rechteck jeweils zu einem Quadrat mit Seitenlänge 3cm:''''' | |
| − | + | Applet | |
| − | + | ||
| − | + | *Die beiden Quadrate sind zerlegungs-gleich | |
| + | |||
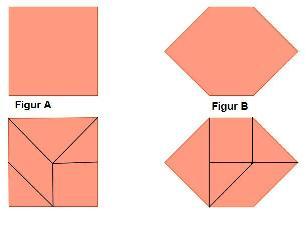
| + | *'''''Wenn man zum Trapez und zum Rechteck jeweils kongruente Figuren (Dreiecke) <span style="color: green">hinzufügt</span> - also <span style="color: green">ergänzt</span>, so sind die beiden <span style="color: green">entstehenden Figuren</span> auch <span style="color: green">zerlegungsgleich</span>''''' (Bild) | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | *'''''Das Trapez und das Rechteck nennt man daher auch <span style="color: green">ergänzungsgleich</span>. ''''' | ||
| + | |||
| + | |||
| + | <div style="border: 2px solid red; background-color:#ffffff; padding:7px;"> | ||
| + | {| | ||
| + | |[[Bild:Ebert_MotivatorMerke.jpg|100px]]|| | ||
| + | *'''<span style="color: red">Figuren sind ergänzungsgleich</span>, wenn man sie durch <span style="color: red">Ergänzung</span> mit der <span style="color: red">gleichen Zahl kongruenter Figuren</span> in <span style="color: red">zerlegungsgleiche Figuren</span> umwandeln kann. ''' | ||
| + | *'''Ergänzungsgleiche Figuren sind zerlegungsgleich.''' | ||
|} | |} | ||
</div> | </div> | ||
Version vom 25. Juli 2009, 13:23 Uhr
- Übertrage folgende Definition in Dein Heft:
 |
Zerlegungsgleichheit von Figuren
Zwei Figuren sind zerlegungsgleich, wenn sie in paarweise kongruente Teilfiguren zerlegt werden können. |
Anwendung der Zerlegungsgleichheit
- Maja weiß jetzt, wozu man die Zerlegungsgleichheit von Figuren nutzen kann. Lies, was sie Dir erzählen möchte:
 |
Damit ist der Flächeninhalt 4(cm²)
|
Ergänzungsgleichheit von Figuren
Zeige, dass das Rechteck und das Trapez zerlegungsgleich sind Applet
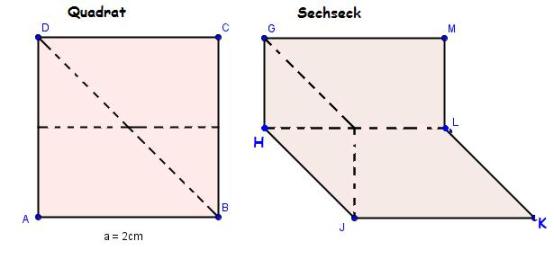
Ergänze das Trapez und das Rechteck jeweils zu einem Quadrat mit Seitenlänge 3cm: Applet
- Die beiden Quadrate sind zerlegungs-gleich
- Wenn man zum Trapez und zum Rechteck jeweils kongruente Figuren (Dreiecke) hinzufügt - also ergänzt, so sind die beiden entstehenden Figuren auch zerlegungsgleich (Bild)
- Das Trapez und das Rechteck nennt man daher auch ergänzungsgleich.
|
|
Auf der nächsten Seite kannst Du dein Wissen testen und zeigen, was Du gelernt hast:
→Übung zur Zerlegungsgleichheit
'Hier geht es zurück zur 'Zerlegungsgleichheit von Figuren
