|
|
| Zeile 48: |
Zeile 48: |
| | Du brauchst doch sicher nicht den Lösungshinweis, oder?<br> | | Du brauchst doch sicher nicht den Lösungshinweis, oder?<br> |
| | {{ versteckt| | | {{ versteckt| |
| − | [[Bild:Ebert_RechteckundTrapez.jpg|Ebert_RechteckundTrapez.jpg]]<br> | + | [[Bild:Ebert_ZerlegungLösung.jpg]]<br> |
| | '''Dies ist eine Lösungsmöglichkeit zur Zerlegung.''' | | '''Dies ist eine Lösungsmöglichkeit zur Zerlegung.''' |
| | }} | | }} |
| Zeile 62: |
Zeile 62: |
| | Vergleiche Deine Lösung hier: <br> | | Vergleiche Deine Lösung hier: <br> |
| | {{ versteckt| | | {{ versteckt| |
| − | [[Bild:Ebert_Quadrate.jpg|Ebert_Quadrate.jpg]] | + | [[Bild:Ebert_ErgänzungHinweis.jpg]] |
| | '''Dies ist eine Lösungsmöglichkeit für die Ergänzung zum Quadrat.''' | | '''Dies ist eine Lösungsmöglichkeit für die Ergänzung zum Quadrat.''' |
| | }} | | }} |
Version vom 29. Juli 2009, 12:54 Uhr
- Übertrage folgende Definition in Dein Heft:
 |
Zerlegungsgleichheit von Figuren
Zwei Figuren sind zerlegungsgleich, wenn sie in paarweise kongruente Teilfiguren zerlegt werden können.
Beispiel:
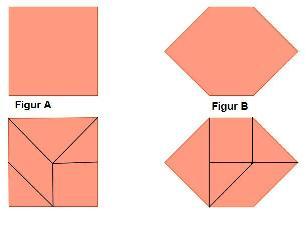
- Figur A und Figur B sind zerlegungsgleich.
- Zerlegungsgleiche Figuren besitzen den gleichen Flächeninhalt
|
Anwendung der Zerlegungsgleichheit
- Maja weiß jetzt, wozu man die Zerlegungsgleichheit von Figuren nutzen kann. Lies, was sie Dir erzählen möchte:
 |
- Ich weiß bereits, wie man den Flächeninhalt von Quadraten berechnet, wenn die Seitenlänge gegeben ist.
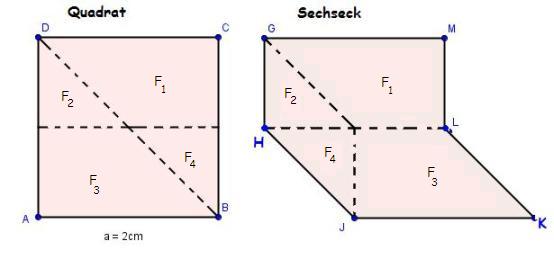
- Die Länge der Seite a des Quadrates ist 2 cm.
Der Flächeninhalt des Quadrates ist4(Zahl eintragen)cm²
- Da das nebenstehende Sechseck zerlegungsgleich zum Quadrat ist und damit den gleichen Flächeninhalt wie das Quadrat besitzt. kennen wir auch den Flächeninhalt des Sechsecks.
Damit ist der Flächeninhalt des Sechsecks4(Zahl eintragen)cm²
- Figuren, von denen man keine Flächeinhaltsformel kennt, wandelt man durch Zerlegung in kongruente Teilfiguren so um, so dass man eine Figur erhält, deren Flächeninhalt wir bereits berechnen können
|
Ergänzungsgleichheit von Figuren
|
|
- Zeige, dass das Rechteck und das Trapez zerlegungsgleich sind
Du brauchst doch sicher nicht den Lösungshinweis, oder?
[Anzeigen][Verstecken]
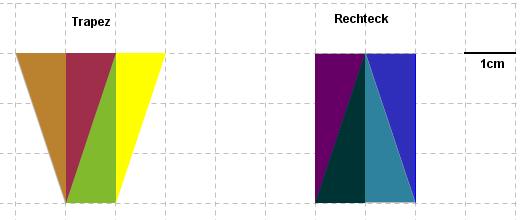
Dies ist eine Lösungsmöglichkeit zur Zerlegung.
- Ergänze das Trapez und das Rechteck jeweils zu einem Quadrat mit Seitenlänge 3cm:
Vergleiche Deine Lösung hier:
[Anzeigen][Verstecken]
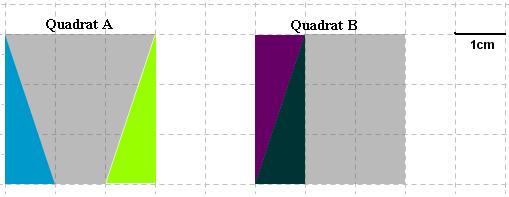 Dies ist eine Lösungsmöglichkeit für die Ergänzung zum Quadrat.
Dies ist eine Lösungsmöglichkeit für die Ergänzung zum Quadrat.
- Welche Eigenschaft haben die Quadrate?'
- Die beiden Quadrate sind zerlegungs-gleich
|
- Wenn man zum Trapez und zum Rechteck jeweils kongruente Figuren hinzufügt - also ergänzt, so sind die beiden entstehenden Quadrate A und B auch zerlegungsgleich
- Das Trapez und das Rechteck nennt man daher auch ergänzungsgleich.
|
 |
- Figuren sind ergänzungsgleich, wenn man sie durch Ergänzung mit der gleichen Zahl kongruenter Figuren in zerlegungsgleiche Figuren umwandeln kann.
- Ergänzungsgleiche Figuren sind zerlegungsgleich.
|
Auf der nächsten Seite kannst Du dein Wissen testen und zeigen, was Du gelernt hast:
→Übung zur Zerlegungsgleichheit
'Hier geht es zurück zur 'Zerlegungsgleichheit von Figuren








