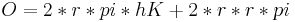Oberfläche des Zylinders: Unterschied zwischen den Versionen
(Merksatz) |
(2. Aufgabe) |
||
| Zeile 1: | Zeile 1: | ||
| − | Hier werden wir uns nun um die Oberfläche des Zylinders kümmern. Du benötigst dafür dein Schulheft und Stifte | + | Hier werden wir uns nun um die Oberfläche des Zylinders kümmern. Du benötigst dafür dein Schulheft, einen Zirkel und Stifte |
<div style="border: 2px solid blue; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid blue; background-color:#ffffff; padding:7px;"> | ||
| Zeile 32: | Zeile 32: | ||
<br> | <br> | ||
<br> | <br> | ||
| + | </div> | ||
| + | <br> | ||
| + | <div style="border: 2px solid blue; background-color:#ffffff; padding:7px;"> | ||
| + | ==2. Aufgabe== | ||
| + | Hier siehst du nun ein Netz eines Zylinders, also die Oberfläche. | ||
| + | <br> | ||
| + | Übertrage dieses Netz in den Schulheft, wähle als Radius 1,5cm, als Länge der Mantelfläche 9,4cm und als Höhe der Mantelfläche 3,5cm. | ||
| + | Benenne die für unsere Formel wichtigen Längen (r, hK). | ||
</div> | </div> | ||
<br> | <br> | ||
Version vom 16. November 2009, 11:13 Uhr
Hier werden wir uns nun um die Oberfläche des Zylinders kümmern. Du benötigst dafür dein Schulheft, einen Zirkel und Stifte
1. Aufgabe
In der letzten Stunde haben wir die Mantelfläche des Zylinders kennengelernt. Nun wollen wir diese zur Oberfläche erweitern.
Findet die unverdrehte Lösung zu den verdrehten Wörtern!
Um die Oberfläche zu berechnen benötigen wir die Mantelfläche, die Grundfläche und die Deckfläche.
Die Grund- und Deckfläche besteht aus je einem Kreis. Die Formel für den Flächeninhalt des Kreises ist uns schon bekannt,
wir haben ihn ausserdem im 1. Lernpfad wiederholt.
Also erhalten wir die Oberfläche, indem wir zu der Mantelfläche die zwei Kreise addieren.
Somit ergibt sich als Formel für die Oberfläche O=2*r*pi*hK+2*r²*pi.
2. Aufgabe
Hier siehst du nun ein Netz eines Zylinders, also die Oberfläche.
Übertrage dieses Netz in den Schulheft, wähle als Radius 1,5cm, als Länge der Mantelfläche 9,4cm und als Höhe der Mantelfläche 3,5cm.
Benenne die für unsere Formel wichtigen Längen (r, hK).
30px Merke
Übertrage diese Formel bitte in dein Schulheft unter der Überschrift "Oberfläche des Zylinders". |