Lineare Gleichungssysteme grafisch lösen/Station 4: Unterschied zwischen den Versionen
| Zeile 2: | Zeile 2: | ||
<div style="border: 2px solid #0000ee; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid #0000ee; background-color:#ffffff; padding:7px;"> | ||
| + | |||
| + | Hier sind wieder zwei Geraden f(x) und g(x) dargestellt. Mit den Schiebereglern kannst du die Steigung ( m ) und den y- Achsenabschnitt ( t ) der Geraden verändern. | ||
<ggb_applet height="500" width="900" showResetIcon="true" filename="Sarah_Hatos_L1_S4.ggb" /> | <ggb_applet height="500" width="900" showResetIcon="true" filename="Sarah_Hatos_L1_S4.ggb" /> | ||
Version vom 9. Dezember 2009, 20:36 Uhr
Station 4
Hier sind wieder zwei Geraden f(x) und g(x) dargestellt. Mit den Schiebereglern kannst du die Steigung ( m ) und den y- Achsenabschnitt ( t ) der Geraden verändern.
In den folgenden Zeichungen sind verschiedene Lineare Gleichungssyteme grafisch dargestellt. Versuche die nebenstehenden Lückentexte auszufüllen. Was fällt dir auf?
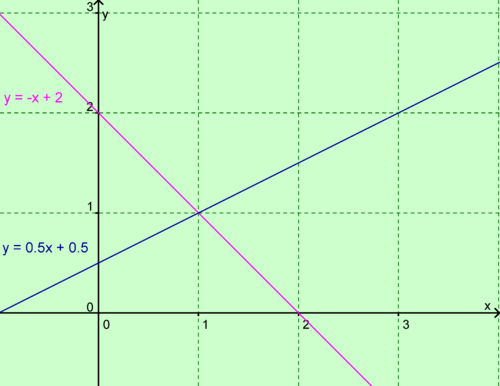 |
Die Geraden haben einen Schnittpunkt. Die Steigung der beiden Geraden ist unterschiedlich. Die Lösungsmenge lautet L={(1/1)}. |
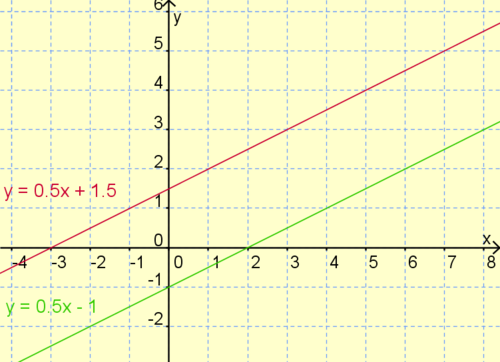 |
Die Geraden haben keinen Schnittpunkt. Die Steigung der beiden Geraden ist gleich. Die Lösungsmenge lautet L={ }. |
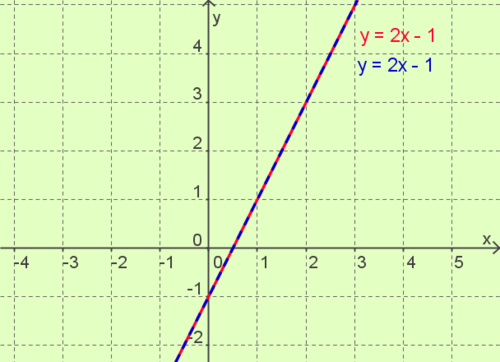 |
Die Geraden haben sind identisch.
Die Lösungsmenge lautet |
Versuche nun die zwei folgenden Fragen zu beantworten! 
1. Frage: Welche Fälle können auftreten? (Das Lineare Gleichungssystem ist eindeutig lösbar) (Das Lineare Gleichungssytem ist unerfüllbar, d.h. keine Lösung) (Das Lineare Gleichungssystem hat unendlich viele Lösungen) (!Das Lineare Gleichungssystem hat 2 Lösungen)
2. Frage: Wieviele verschiedene Möglichkeiten für die Lösungsmenge eines Linearen Gleichungssystems gibt es also? (!1) (!2) (3) (!4)
..

